UVA1646-Edge Case（递推+斐波那契数列）

Posted 2021-02-10 npugen

Problem UVA1646-Edge Case

Time Limit: 3000 mSec

Problem Description

 

 

Input

For each test case, you get a single line containing one positive integer: n, with 3 ≤ n ≤ 10000.

 

 Output

For each test case, a row containing the number of matchings in Cn.

 

 Sample Input

3

4

100

Sample Output

4
7
792070839848372253127

 

题解：这个题一看样例就知道涉及高精度，不过只有加法，即便用C++写也没有什么难度，大致看了一下网上的题解，都是只说找规律没有证明（可能是我没翻到），因此在这里简单做个说明。

 

 

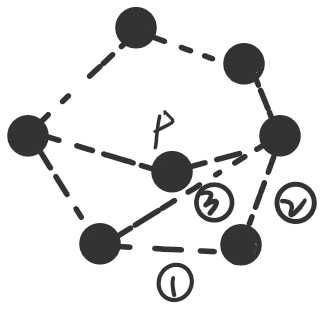
首先设最终结果为a[n]，递推过程中需要引入一个中间序列b[n]，b[n]的含义是强制让1、2两条边不连的匹配数。由此我们得到第一个递推式：

a[n] = b[n] + 2*b[n-1]

解释一下，n的时候的所有成立的情况可以分为三类，

1、1号边和2号边都不连

2、1号边连，2号边不连

3、2号边连，1号边不连

第一种情况自然对应b[n]，第二种情况，如果1连，则1的左右两条边都不能连，这时看我引入的点P以及它连出的线段，它们将多边形分成上下两部分，只看上半部分，第二种情况的情况数就等于上半部分多边形强制让点P连的线段不连的情况数，即b[n-1]，第三种情况类似。

我们再找一个关系式就可以递推了。从第一种情况入手，第一种情况等价于只有n-1个点时3号边不连，那我们就求强制让3不连的匹配数，发现不太好求，那就求强制让3连的匹配数，如果3号边连，那么它左右两条边都不能连，因此类似刚才的分析，匹配数等于b[n-1-1]=b[n-2]，这样一来得到如下关系式：

b[n] = a[n-1]-b[n-2]

有了这两个关系式，解出数列a即可，基本操作，不再赘述。

 1 #include <bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 const int maxn = 10000 + 100;
 6 
 7 int Fib[maxn][15010];
 8 int n;
 9 
10 void prepare()
11 {
12     Fib[3][0] = 1;
13     Fib[3][1] = 4;
14     Fib[4][0] = 1;
15     Fib[4][1] = 7;
16     for (int i = 5; i < maxn; i++)
17     {
18         for (int j = 1; j <= max(Fib[i - 1][0], Fib[i - 2][0]); j++)
19         {
20             Fib[i][j] += Fib[i - 1][j] + Fib[i - 2][j];
21             Fib[i][j + 1] = Fib[i][j] / 10;
22             Fib[i][j] %= 10;
23         }
24         Fib[i][0] = max(Fib[i - 1][0], Fib[i - 2][0]);
25         if (Fib[i][Fib[i][0] + 1])
26             Fib[i][0]++;
27     }
28 }
29 
30 int main()
31 {
32     //freopen("input.txt", "r", stdin);
33     //freopen("output.txt", "w", stdout);
34     prepare();
35     while (~scanf("%d", &n))
36     {
37         for (int i = Fib[n][0]; i; i--)
38             printf("%d", Fib[n][i]);
39         printf("
");
40     }
41     return 0;
42 }