浅谈Tarjan

Posted 2021-02-10 weakest-konjac

有向图强连通分量的Tarjan算法 [有向图强连通分量]

在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

例如：下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。 

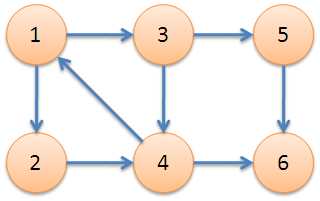
定义DFN(u)为节点u搜索被搜索到时的次序编号，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。由定义可以得出，

Low(u)=Min{
   DFN(u),（第一次被搜索到）
   Low(v),(u,v)为树枝边，u为v的父节点
   DFN(v),(u,v)为指向栈中节点的后向边(非横叉边)（即沿着u搜到v时，发现v已经被搜过了，也就是说形成了一个环）
}
当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。
让我们来模拟一下：
从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

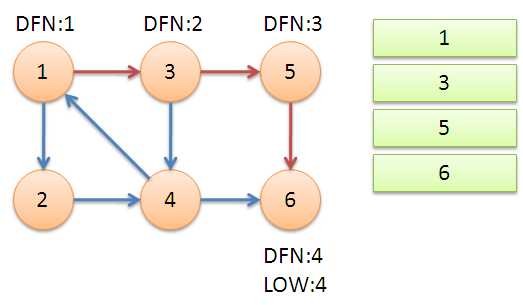
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

 

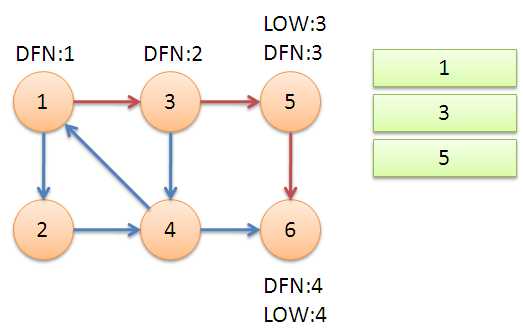
返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

 

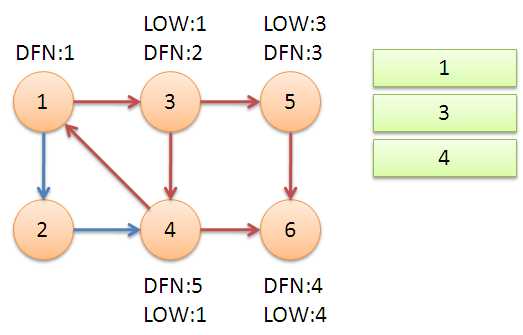
（1，3，4的low都是1，已经说明它们是一个连通分量）
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

 

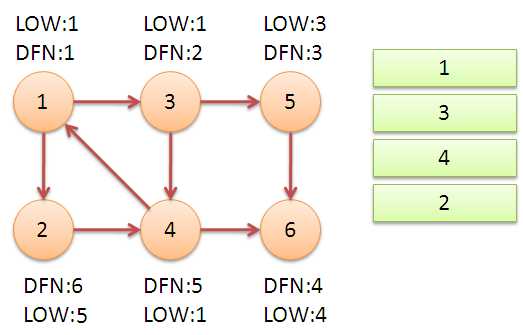
至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。
附录：Tarjan模板
https://www.cnblogs.com/Weakest-konJac/p/10400235.html