白葡萄酒质量评估——回归解决
Posted wyy1480
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了白葡萄酒质量评估——回归解决相关的知识,希望对你有一定的参考价值。
从UCI下载数据集:Wine Quality Data Set ,里面包含红葡萄酒和白葡萄酒的2个样本数据集。里面均包含葡萄酒的11个物理化学方面的因素,还有1个对葡萄酒质量的测评平均分数(0-10分)。现采用其白葡萄酒数据,对该数据集进行一定的数据分析:
(1)建立回归模型,研究这些性质是怎样影响白葡萄酒的质量评价
(2)找出影响较大的前三因素
(3)这些物理化学性质之间是否存在一定的关系
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["font.sans-serif"]=["SimHei"] #正常显示中文标签
plt.rcParams["axes.unicode_minus"]=False #正常显示负号
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")#导入数据
data = pd.read_csv(r"G:UCI dataWine Qualitywinequality-white.csv", sep=";")下面先观察一下白葡萄酒数据:
data.head()| fixed acidity | volatile acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.0 | 0.27 | 0.36 | 20.7 | 0.045 | 45.0 | 170.0 | 1.0010 | 3.00 | 0.45 | 8.8 | 6 |
| 1 | 6.3 | 0.30 | 0.34 | 1.6 | 0.049 | 14.0 | 132.0 | 0.9940 | 3.30 | 0.49 | 9.5 | 6 |
| 2 | 8.1 | 0.28 | 0.40 | 6.9 | 0.050 | 30.0 | 97.0 | 0.9951 | 3.26 | 0.44 | 10.1 | 6 |
| 3 | 7.2 | 0.23 | 0.32 | 8.5 | 0.058 | 47.0 | 186.0 | 0.9956 | 3.19 | 0.40 | 9.9 | 6 |
| 4 | 7.2 | 0.23 | 0.32 | 8.5 | 0.058 | 47.0 | 186.0 | 0.9956 | 3.19 | 0.40 | 9.9 | 6 |
data.info()<class ‘pandas.core.frame.DataFrame‘>
RangeIndex: 4898 entries, 0 to 4897
Data columns (total 12 columns):
fixed acidity 4898 non-null float64
volatile acidity 4898 non-null float64
citric acid 4898 non-null float64
residual sugar 4898 non-null float64
chlorides 4898 non-null float64
free sulfur dioxide 4898 non-null float64
total sulfur dioxide 4898 non-null float64
density 4898 non-null float64
pH 4898 non-null float64
sulphates 4898 non-null float64
alcohol 4898 non-null float64
quality 4898 non-null int64
dtypes: float64(11), int64(1)
memory usage: 459.3 KB1.看到:
(1)数据集中总共有4898个白葡萄酒的样本数据。其中,包含11个物理化学的特征和1个葡萄酒质量评分。
分别为:
- fixed acidity 非挥发性酸
- volatile acidity 挥发性酸
- citric acid 柠檬酸
- residual sugar 剩余糖分
- chlorides 氯化物
- free sulfur dioxide 游离二氧化硫
- total sulfur dioxide 总二氧化硫
- density 密度
- pH 酸碱性
- sulphates 硫酸盐
- alcohol 酒精
- quality 质量
(2)数据完整,无缺失值。注意到,有些数值小于0.1,有些数值大于100。在做回归模型时,我们常用MSE(均方误差)来衡量模型的好坏,如果数据量纲不一样,可能影响我们对模型的评估,所以后面我们将对数据进行归一化处理,排除量纲带来的影响。
(3)11个因素均为浮点型数据,最后的质量评分为整型数据。
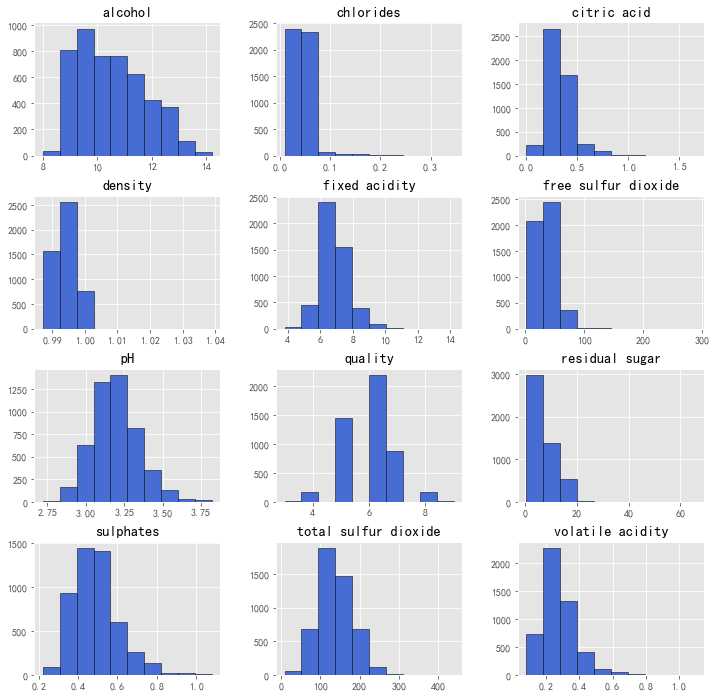
下面通过计算均值、方差、最小最大值等,配合数据的分布直方图来看数据的大致分布:
data.describe()| fixed acidity | volatile acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 |
| mean | 6.854788 | 0.278241 | 0.334192 | 6.391415 | 0.045772 | 35.308085 | 138.360657 | 0.994027 | 3.188267 | 0.489847 | 10.514267 | 5.877909 |
| std | 0.843868 | 0.100795 | 0.121020 | 5.072058 | 0.021848 | 17.007137 | 42.498065 | 0.002991 | 0.151001 | 0.114126 | 1.230621 | 0.885639 |
| min | 3.800000 | 0.080000 | 0.000000 | 0.600000 | 0.009000 | 2.000000 | 9.000000 | 0.987110 | 2.720000 | 0.220000 | 8.000000 | 3.000000 |
| 25% | 6.300000 | 0.210000 | 0.270000 | 1.700000 | 0.036000 | 23.000000 | 108.000000 | 0.991723 | 3.090000 | 0.410000 | 9.500000 | 5.000000 |
| 50% | 6.800000 | 0.260000 | 0.320000 | 5.200000 | 0.043000 | 34.000000 | 134.000000 | 0.993740 | 3.180000 | 0.470000 | 10.400000 | 6.000000 |
| 75% | 7.300000 | 0.320000 | 0.390000 | 9.900000 | 0.050000 | 46.000000 | 167.000000 | 0.996100 | 3.280000 | 0.550000 | 11.400000 | 6.000000 |
| max | 14.200000 | 1.100000 | 1.660000 | 65.800000 | 0.346000 | 289.000000 | 440.000000 | 1.038980 | 3.820000 | 1.080000 | 14.200000 | 9.000000 |
plt.style.use("ggplot")
data.hist(figsize=(12,12), color="#476DD5", edgecolor="k")array([[<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC2FA22A58>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC3044CCF8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC304A54E0>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30509F28>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30B664A8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30B664E0>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30C2D4A8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30C90C18>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30CF9080>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30D6CDD8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30DD3828>,
<matplotlib.axes._subplots.AxesSubplot object at 0x000000EC30E0FCC0>]], dtype=object)
data.skew().sort_values(ascending=False)chlorides 5.023331
volatile acidity 1.576980
free sulfur dioxide 1.406745
citric acid 1.281920
residual sugar 1.077094
density 0.977773
sulphates 0.977194
fixed acidity 0.647751
alcohol 0.487342
pH 0.457783
total sulfur dioxide 0.390710
quality 0.155796
dtype: float64(data.max()-data.min()).sort_values(ascending=False)total sulfur dioxide 431.00000
free sulfur dioxide 287.00000
residual sugar 65.20000
fixed acidity 10.40000
alcohol 6.20000
quality 6.00000
citric acid 1.66000
pH 1.10000
volatile acidity 1.02000
sulphates 0.86000
chlorides 0.33700
density 0.05187
dtype: float642.从均值、标准差、四分位数等值,及直方图看到:
(1)所有的特征都不是正态分布,均呈现右偏。chlorides(氯化物)的右偏程度最大,为5.02,接着是volatile acidity(挥发性酸):1.58 、free sulfur dioxide(游离二氧化硫):1.41;右偏最小的三个特征为:total sulfur dioxide(总二氧化硫0.39)< PH(酸碱度0.46)< alcohol(酒精0.49)。
(2)每个特征的极差(最大值减去最小值的值)相差较大,最大的为total sulfur dioxide(总二氧化硫):431,最小的为density(密度),仅为0.05。后面将对数据进行归一化处理,消除量纲影响。
(3)从四分位数来看,可能存在异常值。为了便于观察,下面进行归一化,借用箱线图来看数据的集中分布情况、异常值的情况。
(4)质量评分最小值为3,最大值为9。50%的评分为5或6分,看出大多数白葡萄酒质量处于中等水平,不会太差,也不会太好。
下面对数据进行标准化处理,让数据减去其均值再除以其对应的标准差:
from sklearn.preprocessing import scale
data_scaled = scale(data)
data_scaledarray([[ 1.72096961e-01, -8.17699008e-02, 2.13280202e-01, ...,
-3.49184257e-01, -1.39315246e+00, 1.37870140e-01],
[ -6.57501128e-01, 2.15895632e-01, 4.80011213e-02, ...,
1.34184656e-03, -8.24275678e-01, 1.37870140e-01],
[ 1.47575110e+00, 1.74519434e-02, 5.43838363e-01, ...,
-4.36815783e-01, -3.36667007e-01, 1.37870140e-01],
...,
[ -4.20473102e-01, -3.79435433e-01, -1.19159198e+00, ...,
-2.61552731e-01, -9.05543789e-01, 1.37870140e-01],
[ -1.60561323e+00, 1.16673788e-01, -2.82557040e-01, ...,
-9.62604939e-01, 1.85757201e+00, 1.26711420e+00],
[ -1.01304317e+00, -6.77100966e-01, 3.78559282e-01, ...,
-1.48839409e+00, 1.04489089e+00, 1.37870140e-01]])plt.figure(figsize=(17,9))
columns = ["非挥发性酸","挥发性酸","柠檬酸","剩余糖分","氯化物","游离二氧化硫","总二氧化硫",
"密度","酸碱性","硫酸盐","酒精","质量"]
plt.boxplot(data_scaled,
showmeans=True,meanprops={"marker":"D","markerfacecolor":"red"},#设置均值点的属性,点的形状、填充色
labels=columns
)
plt.title("归一化后数据的箱线图",color="#4013AF",size=18)
plt.yticks(fontsize=14,color="k")
plt.xticks(fontsize=14.5,color="#081073")(array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]),
<a list of 12 Text xticklabel objects>)
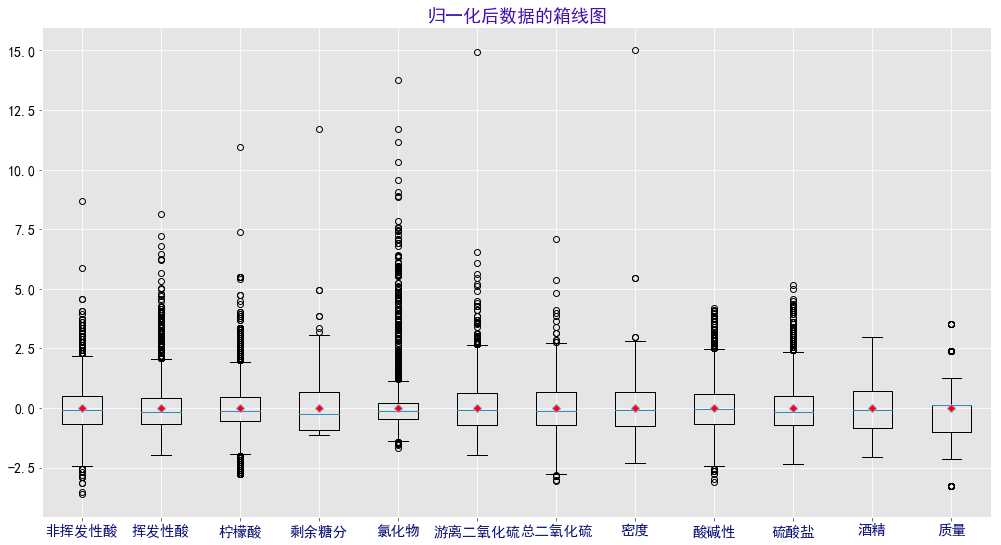
3.对数据进行归一化后,绘制箱线图后发现,除了酒精,其余的变量都存在异常值,且普遍存在较多较大的异常值。
(1)其中,氯化物的箱体最扁,说明50%的数据在均值附近波动,但是存在大量较大的异常值,偏离均值分布。
(2)而剩余糖分、总二氧化硫、密度、质量评分的异常值相对其他特征来说,比较少,且普遍远大于平均值。
(3)非挥发性酸、柠檬酸、酸碱性这三个特征都存在大量较大的异常值,但也同时存在部分较小的异常值。
(4)挥发性酸、氯化物、游离二氧化硫、硫酸盐这四个特征的异常值普遍较大,只有氯化物存在少量较小的异常值。
(5)酒精特征不存在异常值,也与归一前所做的直方图对应得上。
下面探究一下,各特征间、各特征与质量评分之间的关系:
data_df_scaled = pd.DataFrame(data_scaled,columns=columns)
data_df_scaled.sample(4) #随机抽取5个归一化后的样本数据| 非挥发性酸 | 挥发性酸 | 柠檬酸 | 剩余糖分 | 氯化物 | 游离二氧化硫 | 总二氧化硫 | 密度 | 酸碱性 | 硫酸盐 | 酒精 | 质量 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3933 | 2.186835 | 0.315117 | -1.026313 | -0.156050 | -0.310008 | -0.429751 | -1.679322 | -0.249908 | -1.511848 | 0.264236 | 0.394746 | -2.120618 |
| 1075 | -0.538987 | 1.208114 | -1.191592 | -0.629279 | -0.584661 | -0.429751 | -0.337948 | -1.212925 | 0.210175 | 0.439499 | 1.776304 | 1.267114 |
| 2398 | 1.357237 | 0.811227 | 0.461199 | -0.944765 | -0.996641 | -0.547361 | -1.067467 | -0.958796 | -0.253446 | 0.001342 | 1.126159 | 0.137870 |
| 831 | 0.646153 | -1.073988 | 0.543838 | -0.175768 | -0.401559 | -0.076922 | 0.532769 | -0.176345 | -0.915763 | 1.140552 | 0.801087 | -2.120618 |
corr_df = data_df_scaled.corr()
corr_df| 非挥发性酸 | 挥发性酸 | 柠檬酸 | 剩余糖分 | 氯化物 | 游离二氧化硫 | 总二氧化硫 | 密度 | 酸碱性 | 硫酸盐 | 酒精 | 质量 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 非挥发性酸 | 1.000000 | -0.022697 | 0.289181 | 0.089021 | 0.023086 | -0.049396 | 0.091070 | 0.265331 | -0.425858 | -0.017143 | -0.120881 | -0.113663 |
| 挥发性酸 | -0.022697 | 1.000000 | -0.149472 | 0.064286 | 0.070512 | -0.097012 | 0.089261 | 0.027114 | -0.031915 | -0.035728 | 0.067718 | -0.194723 |
| 柠檬酸 | 0.289181 | -0.149472 | 1.000000 | 0.094212 | 0.114364 | 0.094077 | 0.121131 | 0.149503 | -0.163748 | 0.062331 | -0.075729 | -0.009209 |
| 剩余糖分 | 0.089021 | 0.064286 | 0.094212 | 1.000000 | 0.088685 | 0.299098 | 0.401439 | 0.838966 | -0.194133 | -0.026664 | -0.450631 | -0.097577 |
| 氯化物 | 0.023086 | 0.070512 | 0.114364 | 0.088685 | 1.000000 | 0.101392 | 0.198910 | 0.257211 | -0.090439 | 0.016763 | -0.360189 | -0.209934 |
| 游离二氧化硫 | -0.049396 | -0.097012 | 0.094077 | 0.299098 | 0.101392 | 1.000000 | 0.615501 | 0.294210 | -0.000618 | 0.059217 | -0.250104 | 0.008158 |
| 总二氧化硫 | 0.091070 | 0.089261 | 0.121131 | 0.401439 | 0.198910 | 0.615501 | 1.000000 | 0.529881 | 0.002321 | 0.134562 | -0.448892 | -0.174737 |
| 密度 | 0.265331 | 0.027114 | 0.149503 | 0.838966 | 0.257211 | 0.294210 | 0.529881 | 1.000000 | -0.093591 | 0.074493 | -0.780138 | -0.307123 |
| 酸碱性 | -0.425858 | -0.031915 | -0.163748 | -0.194133 | -0.090439 | -0.000618 | 0.002321 | -0.093591 | 1.000000 | 0.155951 | 0.121432 | 0.099427 |
| 硫酸盐 | -0.017143 | -0.035728 | 0.062331 | -0.026664 | 0.016763 | 0.059217 | 0.134562 | 0.074493 | 0.155951 | 1.000000 | -0.017433 | 0.053678 |
| 酒精 | -0.120881 | 0.067718 | -0.075729 | -0.450631 | -0.360189 | -0.250104 | -0.448892 | -0.780138 | 0.121432 | -0.017433 | 1.000000 | 0.435575 |
| 质量 | -0.113663 | -0.194723 | -0.009209 | -0.097577 | -0.209934 | 0.008158 | -0.174737 | -0.307123 | 0.099427 | 0.053678 | 0.435575 | 1.000000 |
corr_df["质量"].sort_values(ascending=False)质量 1.000000
酒精 0.435575
酸碱性 0.099427
硫酸盐 0.053678
游离二氧化硫 0.008158
柠檬酸 -0.009209
剩余糖分 -0.097577
非挥发性酸 -0.113663
总二氧化硫 -0.174737
挥发性酸 -0.194723
氯化物 -0.209934
密度 -0.307123
Name: 质量, dtype: float64plt.figure(figsize=(12,12))
sns.heatmap(corr_df,linewidths=0.1,square=True,linecolor="white",annot=True,cmap=‘YlGnBu‘,vmin=-1,vmax=1)
plt.title("各特征间的热力图")<matplotlib.text.Text at 0xec313361d0>
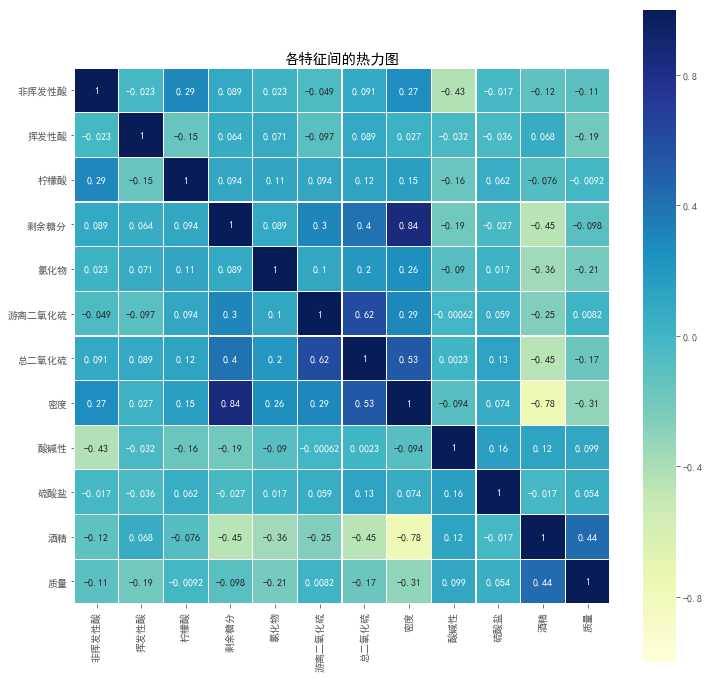
4.可以看到:
(1)白葡萄酒的质量评分与酒精、酸碱性、硫酸盐、游离二氧化硫有正的线性相关关系,它们的含量越高,口感评分越高;而与其他特征都呈现负的线性相关关系,这些特征的含量越高,口感评分越低。关系强度最大为0.44,大部分关系强度的绝对值均小于0.2(线性关系强度在[0,1]之间)。
(2)白葡萄酒的质量评分跟酒精、密度、氯化物的线性关系较强。质量评分与酒精之间有正相关关系,关系强度为0.44,酒精含量越高,口感评分越高;而与密度、氯化物为负线性相关关系,分别为-0.31、-0.21,它们的含量越高,白葡萄酒的口感评分越低。
(3)从热力图看,颜色普遍较浅,说明各变量间的线性相关关系较弱。
(4)而密度跟剩余糖分、酒精线性相关关系比较强。密度与剩余糖分的线性关系为0.84,剩余糖分越多,白葡萄酒的密度越大;密度与酒精的线性关系为-0.78,酒精密度越大,白葡萄酒的密度越小。
下面进行建模,用惩罚性线性回归:套索模型(LassoCV)
x = data_df_scaled.iloc[:,:11]
y = data_df_scaled.iloc[:,-1]
print("特征集:",x.shape)
print("标签集:",y.shape)
from sklearn.linear_model import LassoCV
Las_cv = LassoCV(cv=10).fit(x,y)特征集: (4898, 11)
标签集: (4898,)print("线性模型的截距:",Las_cv.intercept_)
print("线性模型的回归系数:",Las_cv.coef_)线性模型的截距: 1.06646156739e-14
线性模型的回归系数: [ 0.0098704 -0.21381849 0. 0.33369253 -0.01166061 0.06691956
-0.009035 -0.31407498 0.07341963 0.06597724 0.352643 ]5.可以看到,基于归一化后的数据:
(1)我们构造的模型为:
y_scaled = 1.06646156739e-14 + 0.0098704 * x1_scaled - 0.21381849 * x2_scaled + 0.33369253 * x4_scaled -
0.01166061 * x5_scaled + 0.06691956 * x6_scaled - 0.009035 * x7_scaled - 0.31407498 * x8_scaled +
0.07341963 * x9_scaled + 0.06597724 * x10_scaled + 0.352643 * x11_scaled
Coef_df = pd.DataFrame(Las_cv.coef_,index=columns[0:11],columns=["回归系数"])
Coef_df.sort_values(by="回归系数",ascending=False)| 回归系数 | |
|---|---|
| 酒精 | 0.352643 |
| 剩余糖分 | 0.333693 |
| 酸碱性 | 0.073420 |
| 游离二氧化硫 | 0.066920 |
| 硫酸盐 | 0.065977 |
| 非挥发性酸 | 0.009870 |
| 柠檬酸 | 0.000000 |
| 总二氧化硫 | -0.009035 |
| 氯化物 | -0.011661 |
| 挥发性酸 | -0.213818 |
| 密度 | -0.314075 |
(2)柠檬酸的回归系数为0,在LasscoCV模型里,没有对白葡萄酒的口感评价产生影响。酒精、剩余糖分、酸碱性、游离二氧化硫、硫酸盐、非挥发性酸这6个特征对提升口感评价有正向作用,其影响力依次递减;在一定程度上,这些成分含量越多,口感越好。另一方面,密度、挥发性酸、氯化物、总二硫化物对提升口感有负作用,其影响力依次递减;一定程度上,它们在白葡萄酒里的含量越高,口感越差。
(3)对提升白葡萄酒口感评价影响最大的三个特征为:酒精含量、剩余糖分、酸碱性。酒精含量、剩余糖分含量的回归系数分别为0.35、0.33,排名第三的酸碱性的回归系数为0.07,与前面个两个特征相比,该值较小。在实际生产中,为提升白葡萄酒口感,生产商应更多地关注、研究白葡萄酒中的酒精含量和剩余糖分含量。
(4)降低白葡萄酒口感的前三特征为:密度、挥发性酸、氯化物。其中密度的影响最大,为-0.31;挥发性酸的影响第二,为-0.21;氯化物的影响第三,为-0.01。可看到,密度和挥发性酸对降低口感评分的影响较大,氯化物相对较小。在实际生产工艺中,需要更多关注、合理控制白葡萄酒的密度大小与挥发性酸的含量。
(5)在热力图及相关关系计算中,我们得出密度跟剩余糖分(0.84)、酒精(-0.78)的线性相关关系比较强。所以在实际生产中,为了提升口感而不断地提升剩余糖分和酒精含量是不可行的。在提升糖分的同时,要注意密度也有所提升,这时候可适当加入酒精,提高酒精含量来降低密度对口感的影响。应多投入到调配这三个特征的比例,才能更有效地提升白葡萄酒口感,提升销量。
下面来看在十折试验中,MSE的一个变化情况:
plt.figure(figsize=(11,9))
plt.plot(Las_cv.alphas_,Las_cv.mse_path_,"-")
plt.plot(Las_cv.alphas_,Las_cv.mse_path_.mean(axis=-1),label="均方误差均值:MSE_mean",linewidth=3,color="b")
plt.axvline(Las_cv.alpha_,linestyle="--",label="10折预测最佳表现对应的alpha值")
plt.xlabel("alpha值",size=16)
plt.xticks(size=16)
plt.ylabel("均方误差(MSE)")
plt.legend(loc="best")
plt.semilogx()
ax = plt.gca()
ax.invert_xaxis()
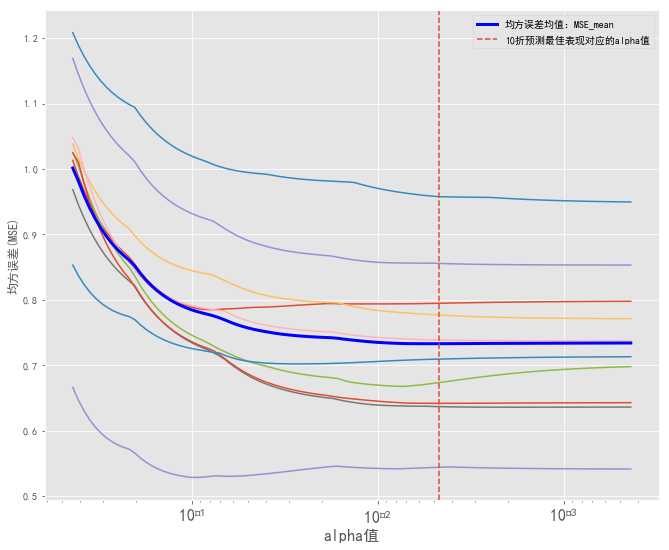
均方误差随着alpha的减小,渐渐地趋于一定的值,处于基本稳定状态。
Las_cv.alpha_0.0046705249012570426在众多的拟合的惩罚系数里,表现最优的惩罚系数为0.0046705249012570426。在这个位置,均方误差MSE基本稳定下来。
总的来说:
(1)各特征间存在一定的线性关系,但普遍关系强度不太大;最大的是密度与剩余糖分(0.84)、酒精浓度(-0.78)的线性关系。
(2)找出对白葡萄酒口感影响最大的前三因素:酒精、剩余糖分、密度;
(3)针对给出的11个特征,我们用LassoCV来建模,并给出了最终的模型:
y_scaled = 1.06646156739e-14 + 0.0098704 * x1_scaled - 0.21381849 * x2_scaled + 0.33369253 * x4_scaled -
0.01166061 * x5_scaled + 0.06691956 * x6_scaled - 0.009035 * x7_scaled - 0.31407498 * x8_scaled +
0.07341963 * x9_scaled + 0.06597724 * x10_scaled + 0.352643 * x11_scaled
(4)在实际生产中,厂家应多尝试酒精、剩余糖分、密度的不同比例调配方式。酒精、剩余糖分的含量能提高葡萄酒的口感,而密度大小则会降低酒的口感。另外,要注意到密度跟剩余糖分(0.84)、酒精(-0.78)的相关关系。所以在实际生产中,根据二八定理,针对这三个特征多投入,会得到较大的收益。
以上是关于白葡萄酒质量评估——回归解决的主要内容,如果未能解决你的问题,请参考以下文章