有关字符串的算法（KMP,Manacher,BM）陆续补充

Posted 2021-02-09 virgildevil

KMP算法：

引言：

KMP算法是一种改进的字符串匹配算法     

字符串匹配：即寻找str_target在str_source中出现的位置

没有改进的字符串匹配：用暴力法进行搜索，枚举出所有的情况然后一一比较。缺点：耗费了很多时间，时间复杂度非常高。所以需要改进。

这里举一个暴力匹配的例子：

在"zabcae"中寻找"abcab" :

 

KMP算法优势：

可以看到，每次出现不匹配时，i都会回溯到上一次的位置。而由于前几次比较的结果，可以避免i的回溯，并且找到一个比较好的j的位置进行比较，从而减小

许多重复的运算。

KMP中的NEXT数组：

前面说到 j 会进行回溯，而 j 应该回溯到什么地方呢？

由next[]数组来回答，具体看下图：

可以看到，NEXT[ ]数组保证了i不会回溯，并且j会回溯到较好的一个位置

NEXT[ ]数组的实现：

先给出代码：

 1 void cre_next(char * p/*模式串首地址*/,int len/*模式串长度*/) {  
 2     int j = 0;
 3     int k = -1;
 4     next_[0] = -1;
 5 
 6     while (j < len - 1) {
 7         if ( k==-1 || p[j]==p[k]) {
 8             next_[j + 1] = k + 1;
 9             j++;
10             k++;
11         }
12         else {
13             k = next_[k];
14         }
15 
16     }
17 }

 

看起来一头雾水，接下来我们来一步步分析每句代码的含义。

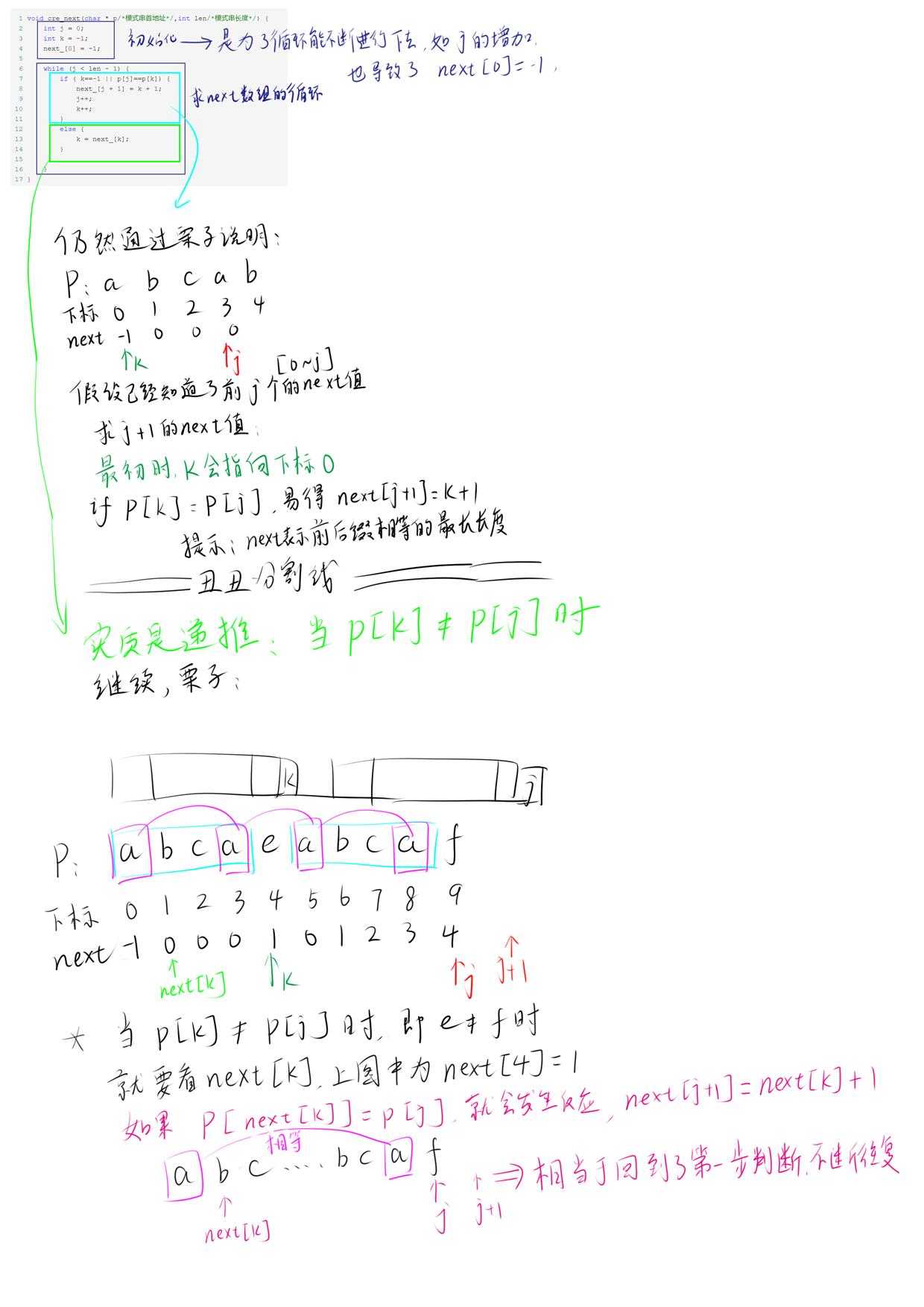
最本质的就是  p[k]=p[j]和p[k]!=p[j]时两种情况的讨论，但经过多人的修改，变成了上面这种代码简洁的形式。

简略来说就是：

当p[k]=p[j]时，next[j+1]=k+1

当p[k]!=p[j]时，k=next[k]  然后回到第一步进行判断。

获取到next数组时实际上就完成了KMP算法的很大一部分，接下来就稍微修改下暴力破解时的代码就好了。

 

2019/2/15更新，未完待续。。。