隐马尔科夫模型与三个问题

Posted 2020-11-01

隐马尔科夫模型定义

隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。

隐藏的马尔可夫链随机生成的状态的序列，称为状态序列（state sequence);每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列（observation sequence)。

序列的每一个位置又可以看作是一个时刻。

下面我们引入一些符号来表示这些定义：

设Q是所有可能的状态的集合，V是所有可能的观测的集合。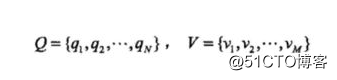

其中，N是可能的状态数，M是可能的观测数。

状态q是不可见的，观测v是可见的。

应用到词性标注中，v代表词语，是可以观察到的。q代表我们要预测的词性（一个词可能对应多个词性）是隐含状态。

应用到分词中，v代表词语，是可以观察的。q代表我们的标签（B,E这些标签，代表一个词语的开始，或者中间等等）

应用到命名实体识别中，v代表词语，是可以观察的。q代表我们的标签（标签代表着地点词，时间词这些）

上面提到的方法，有兴趣的同学可以查阅相应资料。

I是长度为T的状态序列，O是对应的观测序列。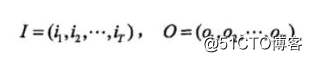

我们可以看做是给定了一个词（O）+词性（I）的训练集。或者一个词(O)+分词标签（I）的训练集....有了训练数据，那么再加上训练算法则很多问题也就可以解决了，问题后面慢慢道来~

我们继续定义A为状态转移概率矩阵：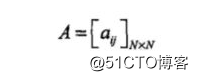

其中，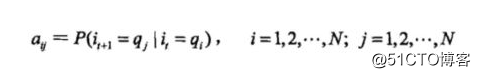

是在时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。

B是观测概率矩阵: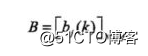

其中，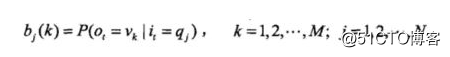

是在时刻t处于状态qj的条件下生成观测vk的概率（也就是所谓的“发射概率”）。

所以我们在其它资料中，常见到的生成概率与发射概率其实是一个概念。

π是初始状态概率向量：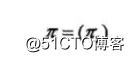

其中，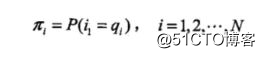

隐马尔可夫模型由初始状态概率向量π、状态转移概率矩阵A和观测概率矩阵B决定。π和A决定状态序列，B决定观测序列。因此，隐马尔可夫模型可以用三元符号表示，即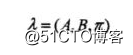

\lambda =(A,B,\Pi )称为隐马尔可夫模型的三要素。
如果加上一个具体的状态集合Q和观测序列V，构成了HMM的五元组，这也是隐马尔科夫模型的所有组成部分。

下面介绍一下隐马尔可夫链的三个基本问题：
1、已知模型求观测序列出现的概率
2、已知观测序列，求模型的参数
3、已知观测序列求可能的状态序列