(寒假开黑gym)2017-2018 ACM-ICPC German Collegiate Programming Contest (GCPC 2017)
Posted luowentao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了(寒假开黑gym)2017-2018 ACM-ICPC German Collegiate Programming Contest (GCPC 2017)相关的知识,希望对你有一定的参考价值。
layout: post
title: (寒假开黑gym)2017-2018 ACM-ICPC German Collegiate Programming Contest (GCPC 2017)
author: "luowentaoaa"
catalog: true
tags:
mathjax: true
- codeforces
B.Buildings (polya定理)
题意
B:给你m面墙,每面墙是n*n的格子,你有c种颜色,问你有多少种涂色方案。用polya定理
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
///a<mod 并且 p为素数
ll pow_mod(ll x, ll n, ll mod){
ll res=1;
while(n){
if(n&1)res=res*x%mod;
x=x*x%mod;
n>>=1;
}
return res;
}
ll inv(ll a,ll p){return pow_mod(a,p-2,p);}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
int n,m,c;
cin>>n>>m>>c;
ll ans=0;
for(int i=0;i<m;i++){
ans+=pow_mod(c,n*n*__gcd(i,m),mod);
ans%=mod;
}
cout<<ans*inv(m,mod)%mod<<endl;
return 0;
}C.Joyride (分层图最短路)
题意
C:游乐场有n个设施,有m条人行道,游乐设施会花费ti的时间和pi的钱,人行道需要花费t的时间,你需要用最少的钱恰好游玩x的时间,起点是1,终点是1,求最少的钱是多少4
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e3+50;
const int inf=1e9+7;
int x,n,m,t;
vector<int>ve[maxn];
struct need{
int t,p;
}ned[maxn];
struct node{
int in;
int w;
int time;
};
int dis[maxn][maxn];
void dij(){
queue<node>q;
q.push(node{1,ned[1].p,ned[1].t});
for(int i=0;i<=1000;i++){
for(int j=0;j<=1000;j++)dis[i][j]=inf;
}
dis[1][ned[1].t]=ned[1].p;
while(!q.empty()){
node now=q.front();
q.pop();
int in=now.in,w=now.w,time=now.time;
if(time+ned[in].t<=x&&w+ned[in].p<dis[in][time+ned[in].t]){
dis[in][time+ned[in].t]=w+ned[in].p;
q.push(node{in,dis[in][time+ned[in].t],time+ned[in].t});
}
for(int i=0;i<ve[in].size();i++){
int nex=ve[in][i];
int nextime=time+t+ned[nex].t;
if(nextime<=x&&dis[nex][nextime]>w+ned[nex].p){
dis[nex][nextime]=w+ned[nex].p;
q.push(node{nex,w+ned[nex].p,nextime});
}
}
}
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
cin>>x>>n>>m>>t;
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
ve[a].push_back(b);
ve[b].push_back(a);
}
for(int i=1;i<=n;i++){
cin>>ned[i].t>>ned[i].p;
}
dij();
if(dis[1][x]==inf)cout<<"It is a trap."<<endl;
else cout<<dis[1][x]<<endl;
return 0;
}D.Pants On Fire (map+dfs,or 传递闭包)
题意
D 有n个已知串,给m个串,让你去判断他们是对的还是错的还是未知的
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e3+50;
const int inf=1e9+7;
map<string,int>mp;
int cnt;
bool ok[500][500];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
string a,b,c,d,e;
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a>>b>>c>>d>>e;
if(!mp[a])mp[a]=++cnt;
if(!mp[e])mp[e]=++cnt;
ok[mp[a]][mp[e]]=true;
}
for(int k=1;k<=cnt;k++){
for(int i=1;i<=cnt;i++){
for(int j=1;j<=cnt;j++){
ok[i][j]|=ok[i][k]&&ok[k][j];
}
}
}
for(int i=1;i<=m;i++){
cin>>a>>b>>c>>d>>e;
if(!mp[a]||!mp[e]){cout<<"Pants on Fire"<<endl;continue;}
int u=mp[a],v=mp[e];
if(ok[u][v])cout<<"Fact"<<endl;
else if(ok[v][u])cout<<"Alternative Fact"<<endl;
else{
cout<<"Pants on Fire"<<endl;
}
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e3+50;
const int inf=1e9+7;
map<string,int>mp;
int cnt;
vector<int>G[maxn];
bool dfs(int u,int v){
for(int i=0;i<G[u].size();i++){
if(G[u][i]==v)return true;
bool ok=dfs(G[u][i],v);
if(ok)return true;
}
return false;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
string a,b,c,d,e;
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a>>b>>c>>d>>e;
if(!mp[a])mp[a]=++cnt;
if(!mp[e])mp[e]=++cnt;
G[mp[a]].push_back(mp[e]);
}
for(int i=1;i<=m;i++){
cin>>a>>b>>c>>d>>e;
if(!mp[a]||!mp[e]){cout<<"Pants on Fire"<<endl;continue;}
int u=mp[a],v=mp[e];
if(dfs(u,v))cout<<"Fact"<<endl;
else if(dfs(v,u))cout<<"Alternative Fact"<<endl;
else{
cout<<"Pants on Fire"<<endl;
}
}
return 0;
}F.Plug It In (匈牙利算法/二分图匹配/网络流)
题意
m个插口,n个电器 k个可以匹配的连接 ,问你最大匹配数,但是你有一次机会把一个接口变成三个一样的
思路
考虑暴力每次暴力把一个其中一个接口数+2跑匈牙利算法,复杂度N^3,然后发现其实第一次跑的最初的图是可以一直重复利用的,然后就直接把后面的多出来的接口拿去跑增广路就行。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
/// 二分图最大基数匹配
int mp[1550][1550];
int link[1550];
int n,m,k;
bool vis[1550];
int remain[1550];
bool match(int u){
for(int i=1;i<=m;i++){
if(vis[i]==0&&mp[u][i]){
vis[i]=1;
if(link[i]==-1||match(link[i])){
link[i]=u;
return 1;
}
}
}
return 0;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
int k;
cin>>n>>m>>k;
memset(link,-1,sizeof(link));
for(int i=1;i<=k;i++){
int a,b;
cin>>a>>b;
mp[a][b]=1;
}
int ans=0;
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if(match(i))ans++;
}
for(int i=1;i<=m;i++){
remain[i]=link[i];
}
int mx=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)mp[n+1][j]=mp[n+2][j]=mp[i][j];
for(int i=1;i<=m;i++){
link[i]=remain[i];
}
int now=0;
memset(vis,0,sizeof(vis));
for(int j=n+1;j<=n+2;j++){
if(match(j))now++;
}
mx=max(now,mx);
}
cout<<ans+mx<<endl;
return 0;
}G.Water Testing (皮克定理)
题意
给你一个多边形问你多边形中的整点个数有多少
思路
皮克定理
皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式,该公式可以表示为2S=2a+b-2,其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积。
其中,面积用每两条线的叉积计算
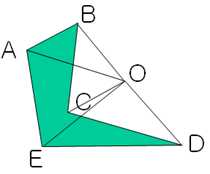
当O点为原点时,根据向量的叉积计算公式,各个三角形的面积计算如下:
S_OAB = 0.5(A_xB_y - A_y*B_x) 【(A_x,A_y)为A点的坐标】
S_OBC = 0.5(B_xC_y - B_y*C_x)
S_OCD = 0.5(C_xD_y - C_y*D_x)
S_ODE = 0.5(D_xE_y - D_y*E_x)
S_OEA = 0.5(E_xA_y - E_y*A_x)
边界的点数用gcd(a.x-b.x,a.y-b.y)计算
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct Point{
ll x,y;
}my[maxn];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>my[i].x>>my[i].y;
}
ll s=0,b=0;
for(int i=0;i<n;i++){
s+=my[i].x*my[(i+1)%n].y-my[(i+1)%n].x*my[i].y;
b+=__gcd(abs(my[i].x-my[(i+1)%n].x),abs(my[i].y-my[(i+1)%n].y));
}
s/=2;
s=abs(s);
cout<<s-b/2+1<<endl;
return 0;
}I.Uberwatch (基础DP)
思路
对于每个点考虑两种情况,如果他不放必杀技那
[
dp[i]=dp[i-1]
]
如果他放必杀技,那么他就只能在i-m时间之前放的最大值加起来
[
dp[i]=dp[i-m]+a[i]
]
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=3e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
int a[maxn];
int dp[maxn];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
int sum=0;
for(int i=m+1;i<=n;i++){
dp[i]=max(dp[i-1],dp[i-m]+a[i]);
}
cout<<dp[n]<<endl;
return 0;
}K.You Are Fired (签到)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=1e5+50;
const ll inf=0x3f3f3f3f3f3f3f3fLL;
struct node{
ll money;
string name;
}my[maxn];
bool vis[maxn];
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
ll n,d,k;
cin>>n>>d>>k;
for(int i=1;i<=n;i++){
cin>>my[i].name>>my[i].money;
}
sort(my+1,my+1+n,[](node a,node b){
return a.money>b.money;
});
ll ans=0,num=0;
for(int i=1;i<=k;i++){
ans+=my[i].money;
vis[i]=true;
num++;
if(ans>=d)break;
}
if(ans<d)cout<<"impossible"<<endl;
else{
cout<<num<<endl;
for(int i=1;i<=n;i++){
if(vis[i])
cout<<my[i].name<<", YOU ARE FIRED!"<<endl;
}
}
return 0;
}以上是关于(寒假开黑gym)2017-2018 ACM-ICPC German Collegiate Programming Contest (GCPC 2017)的主要内容,如果未能解决你的问题,请参考以下文章