matlab从曲线图提取数据

Posted 2021-02-09 shy-

同学用肉体一顿饭让我帮他做下这个DDL

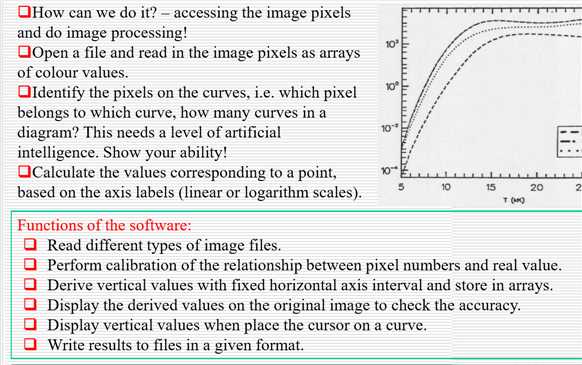
样图是一张非常扭曲的三虚线图他甚至想OCR识别x轴y轴坐标单位

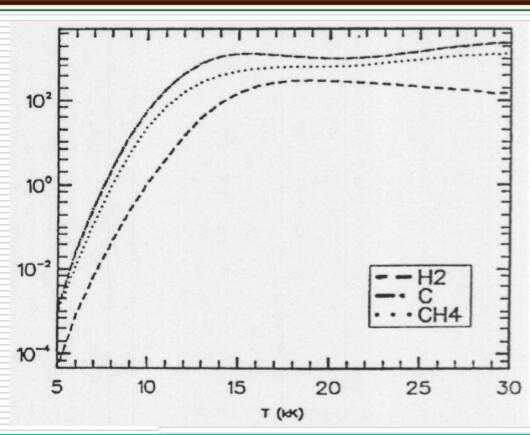
• 上谷歌查了查，对于曲线图提取数据基本上是手动在曲线上取几个点，然后由这个几个点开始遍历领域点，判断领域点是否是黑色，然后再遍历这个黑色点的领域，最终找出一条最长的线便是曲线，一种类似曲线拟合的做法？
• 知乎专栏提供了一种思路，先把曲线图上无关信息去掉，然后提取最大的连通区域，就是所需要的实线，只可惜样例图要做的是虚线。
  第一种方法是同学AA想要的，不过英国人嘛，只告诉他要这样做，并没有告诉他基本思想，所以我们基于第二种方法拓展尝试一下。

清洗图像

所给的图像是RGB图像，且有噪声点，先将图像灰度化，计算图像阈值，通过阈值将图像二值化。

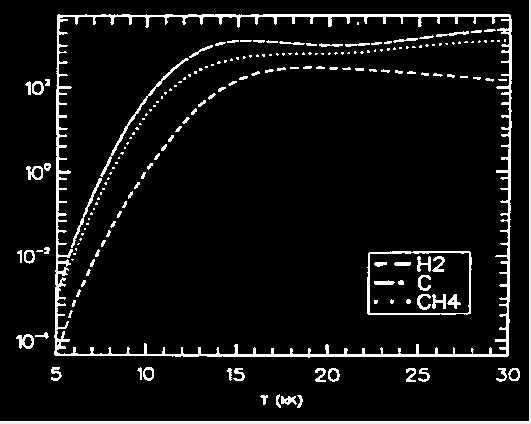
提取真实区域

想要的真实区域就是下图中使用红框标出的区域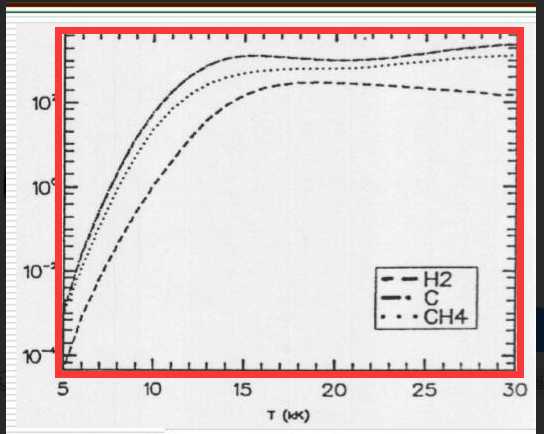

法1

一开始的想法是先在图片的(end*0.8:end-10,)区域中霍夫变换识别出下边框，然后取下边框的(,1:10)部分识别左边框，取左边框的最上端坐标和下边框的最右端坐标，作为分割图像的基准，真实区域就分割出来了。

• 提取下边框很顺利
  
• 提取左边框不是很顺利
  
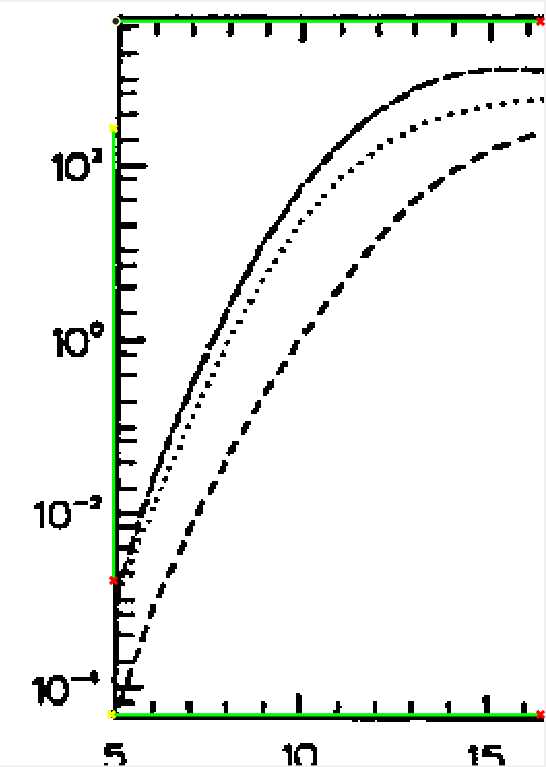
• 提取右边框也不是很顺利
  
• 提取上边框很顺利
  
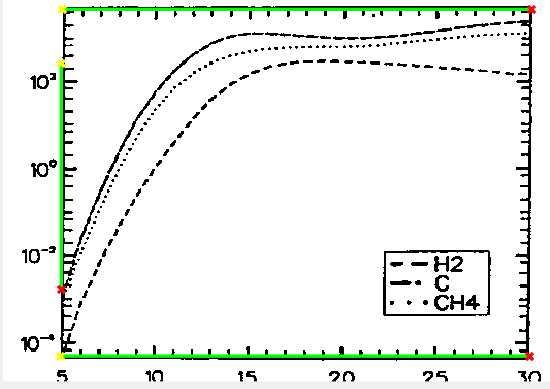
  虽然和计划的有所偏差，但通过上边框的最左端坐标和下边框的最右段坐标，作为分割图像的基准，得到的真实图像理论上是相同的。

法2

对于样例图，真实区域是封闭的，是图中的最大连通区域，那找最大联通区域也可以提取出样例图的真实区域。

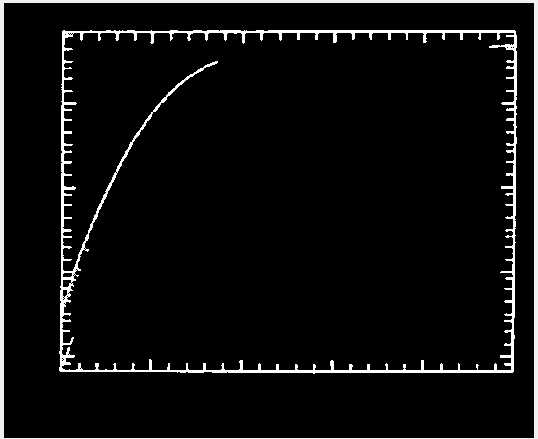
再取得该区域最左上端白点坐标和最右下端白点坐标，作为分割图像的基准，得到真实图像。
真实图像如图所示

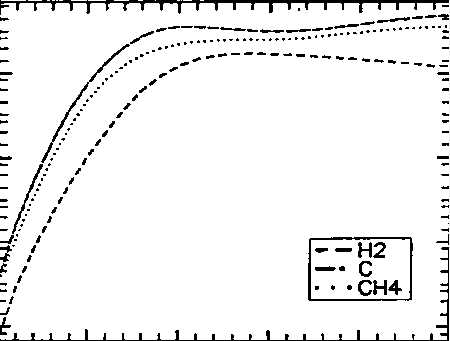
再次清洗图像

为了方便起见，下文中“图”、“图像”指的是上一步中得到的真实图像，而不是原始图像。
对于得到的图像，仍然存在边框、刻度线、右下角标识区域等无关信息。

• 边框可以直接通过上一步法1中得到的边框坐标数组去掉。
• 刻度线以左边框的刻度线为例，遍历图像(,1:5)范围内，若该点是黑点，则从该点开始，向右寻找最大的直线区域，去除。
  样例图中存在曲线与刻度线相交的情况，我采用的方法是对于该点，如果24领域中的黑点总数大于一个阈值，则认为该点是曲线上的点，保留。
• 右下角标识区域直接找取联通区域，如果该连通区域的大小大于阈值，认为是标识区域，去除。
  得到的结果图像，边界存在问题，有待改进：
  

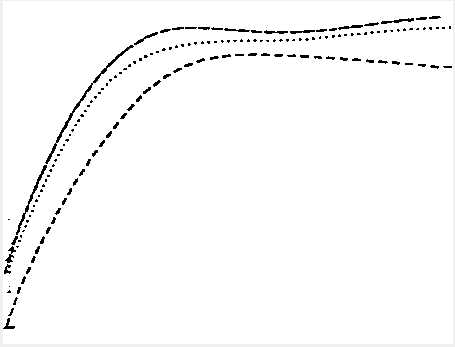
分离曲线

三条曲线都不是实线，没法通过找最大联通区域的方法逐个分离，但因为不同曲线中实线部分的长度是不一样的，所以可以贪心一下，从第1列开始，以某个阈值add_len为步长，找最大连通区域，再进行拼接，以图中最上面一条曲线为例：

• 首先取图像(:,1:10)区域中的最大联通区域，或者取3个联通区域，认为联通区域在列上的坐标极小值为其高度值，高度值越小则越高，最高者则为想要取得最上面一条曲线。
  
• 然后取得该联通区域中最右端的点n1(x,y)，再取(:,y+1:y+add_len)中的n个联通区域，对于每个联通区域，找出其最左端的点n2(x1,y1)，求n1与n2之间的欧式距离，认为欧式距离最短的就是该曲线在(:,y+1:y+add_len)的部分，然后重复该步，直到y值无限接近于图像最右端。
• 对于上一步也有不同的做法，取得该联通区域中最右端的点n1(x,y)，在从i=1开始循环，取(:,y+1:y+add_len)中的i个最大联通区域，对于第i个区域，他的面积总是第i大的，找出其最左端的点n2(x1,y1)，求n1与n2之间的欧式距离，若欧式距离小于某个阈值，则认为该联通区域是该曲线在(:,y+1:y+add_len)的部分，然后重复该步，直到y值无限接近于图像最右端。
  过程如图：
  
  两种做法进行比较，得出的曲线基本相同。
  取得最上端曲线a如图所示：
  
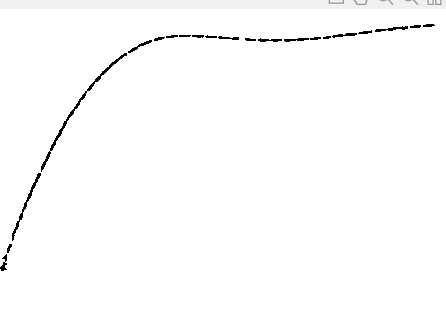
  然后将该曲线在图中去除，再重复之前的做法，取得第二条曲线b。对于第二条曲线，add_len需要改小，欧式距离的阈值需要改大。
  
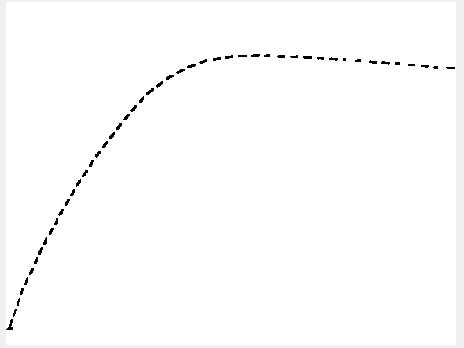
  将第二条曲线去除，得到第三条曲线c
  
  可以看出第三条曲线的图像存在噪点，可以用一个区域对噪点清洗，得到第三条曲线c
  

导出数据

将a,b,c的坐标值与图像的size相除，再乘上单位，即可得到数据。