James Munkres Topology: Sec 22 Exer 3

Posted 2021-02-08 peabody

Exercise 22.3 Let (pi_1: mathbb{R} imes mathbb{R} ightarrow mathbb{R}) be projection on the first coordinate. Let (A) be the subspace of (mathbb{R} imesmathbb{R}) consisting of all points (x imes y) for which either (x geq 0) or (y = 0) (or both); let (q: A ightarrow mathbb{R}) be obtained by restricting (pi_1). Show that (q) is a quotient map that is neither open nor closed.

Proof (a) Show (q) is a quotient map.

The projection map (pi_1) is continuous because the pre-image of any open set (U) in (mathbb{R}) under (pi_1) is (U imes mathbb{R}), which is open in the product space (mathbb{R} imesmathbb{R}). Then its restriction (q) is also continuous due to Theorem 18.2.

According to the illustrated domain of (q) in Figure 1 which is marked in light grey, it is obvious that (q) is surjective. It also shows the three types of saturated open sets in (A) with respect to (q), which are marked in red:

• ((a,b) imes {0}) with (a < 0) and (b leq 0) and its image under (q) is ((a, b)).
• ((a,b) imes mathbb{R}) with (a geq 0) and (b > 0) and its image under (q) is ((a, b)).
• ((a, 0) imes {0} cup [0,b) imes mathbb{R}) with (a < 0) and (b > 0). Because a map preserves set union operation, its image under (q) is ((a, b)).

It can be seen that for the three types of saturated open sets, their images are all open in (mathbb{R}?). Meanwhile, arbitrary union of the above three types saturated open sets is also a saturated open set with its image open in (mathbb{R}?). Therefore, (q?) is a quotient map.

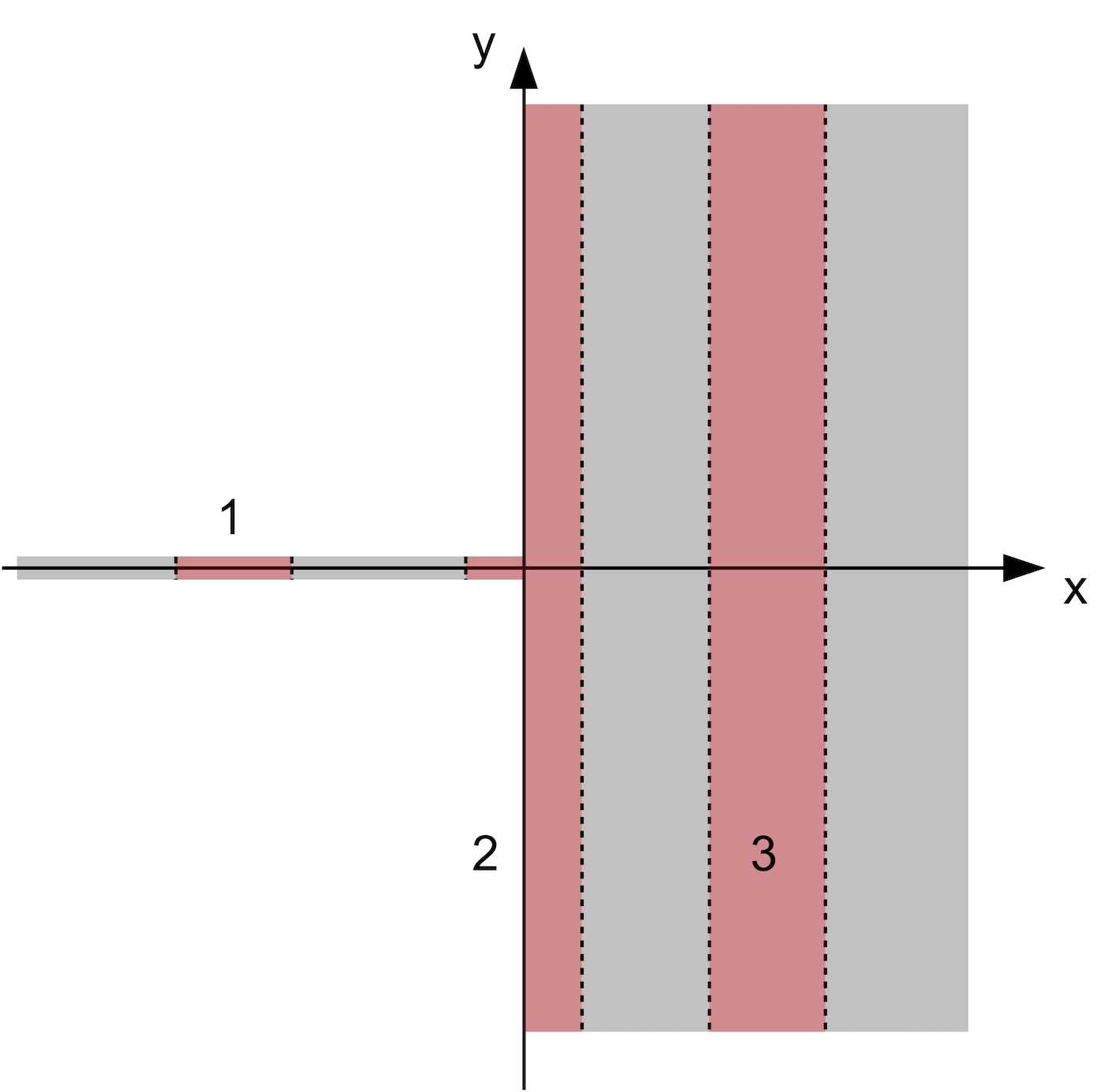
Figure 1. Illustration of the domain of (q) and saturated open sets in (A).

(b) Show (q) is neither an open nor a closed map.

Let (U = [0, 1) imes (1, 2)) be an open set of (A) in the subspace topology, which is not saturated. (q(U) = [0, 1)) is not open in (mathbb{R}). Hence (q) is not an open map.

Let (U = {(x,y) vert xy = 1 ; ext{and}; x > 0 }) which is closed in (mathbb{R} imes mathbb{R}). According to Theorem 17.2, (U) is also closed in the subspace (A). Then (q(U)=(0,+infty)), which is not closed in (mathbb{R}). Hence (q) is not a closed map.

Comment This exercise shows that a function being open or closed map is a sufficient but not a necessary condition for the function to be a quotient map.