Java集合详解6:TreeMap和红黑树
Posted itxiaok
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Java集合详解6:TreeMap和红黑树相关的知识,希望对你有一定的参考价值。
之前的文章讲解了两种Map,分别是HashMap与LinkedHashMap,它们保证了以O(1)的时间复杂度进行增、删、改、查,从存储角度考虑,这两种数据结构是非常优秀的。另外,LinkedHashMap还额外地保证了Map的遍历顺序可以与put顺序一致,解决了HashMap本身无序的问题。
尽管如此,HashMap与LinkedHashMap还是有自己的局限性----它们不具备统计性能,或者说它们的统计性能时间复杂度并不是很好才更准确,所有的统计必须遍历所有Entry,因此时间复杂度为O(N)。比如Map的Key有1、2、3、4、5、6、7,我现在要统计:
-
所有Key比3大的键值对有哪些
-
Key最小的和Key最大的是哪两个
就类似这些操作,HashMap和LinkedHashMap做得比较差,此时我们可以使用TreeMap。TreeMap的Key按照自然顺序进行排序或者根据创建映射时提供的Comparator接口进行排序。TreeMap为增、删、改、查这些操作提供了log(N)的时间开销,从存储角度而言,这比HashMap与LinkedHashMap的O(1)时间复杂度要差些;但是在统计性能上,TreeMap同样可以保证log(N)的时间开销,这又比HashMap与LinkedHashMap的O(N)时间复杂度好不少。
因此总结而言:如果只需要存储功能,使用HashMap与LinkedHashMap是一种更好的选择;如果还需要保证统计性能或者需要对Key按照一定规则进行排序,那么使用TreeMap是一种更好的选择。
红黑树的一些基本概念
在讲TreeMap前还是先说一下红黑树的一些基本概念,这样可以更好地理解之后TreeMap的源代码。
二叉查找树在生成的时候是非常容易失衡的,造成的最坏情况就是一边倒(即只有左子树/右子树),这样会导致树检索的效率大大降低。(关于树和二叉查找树可以看我之前写的一篇文章树型结构)
红黑树是为了维护二叉查找树的平衡而产生的一种树,根据维基百科的定义,红黑树有五个特性,但我觉得讲得不太易懂,我自己总结一下,红黑树的特性大致有三个(换句话说,插入、删除节点后整个红黑树也必须满足下面的三个性质,如果不满足则必须进行旋转):
-
根节点与叶节点都是黑色节点,其中叶节点为Null节点
-
每个红色节点的两个子节点都是黑色节点,换句话说就是不能有连续两个红色节点
-
从根节点到所有叶子节点上的黑色节点数量是相同的
上述的性质约束了红黑树的关键:从根到叶子节点的最长可能路径不多于最短可能路径的两倍长。得到这个结论的理由是:
-
红黑树中最短的可能路径是全部为黑色节点的路径
-
红黑树中最长的可能路径是红黑相间的路径
此时(2)正好是(1)的两倍长。结果就是这个树大致上是平衡的,因为比如插入、删除和查找某个值这样的操作最坏情况都要求与树的高度成比例,这个高度的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树,最终保证了红黑树能够以O(log2 n) 的时间复杂度进行搜索、插入、删除。
官方定义:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
注意: (01) 特性(3)中的叶子节点,是只为空(NIL或null)的节点。 (02) 特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
下面展示一张红黑树的实例图:
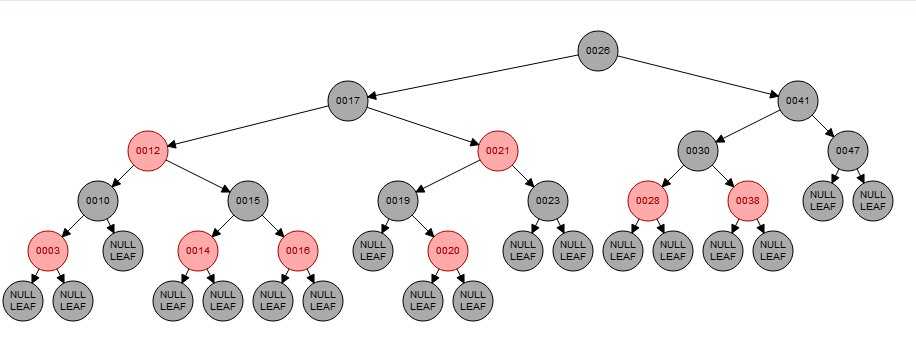
可以看到根节点到所有NULL LEAF节点(即叶子节点)所经过的黑色节点都是2个。
另外从这张图上我们还能得到一个结论:红黑树并不是高度的平衡树。所谓平衡树指的是一棵空树或它的左右两个子树的高度差的绝对值不超过1,但是我们看:
-
最左边的路径0026-->0017-->0012-->0010-->0003-->NULL LEAF,它的高度为5
-
最后边的路径0026-->0041-->0047-->NULL LEAF,它的高度为3
左右子树的高度差值为2,因此红黑树并不是高度平衡的,它放弃了高度平衡的特性而只追求部分平衡,这种特性降低了插入、删除时对树旋转的要求,从而提升了树的整体性能。而其他平衡树比如AVL树虽然查找性能为性能是O(logn),但是为了维护其平衡特性,可能要在插入、删除操作时进行多次的旋转,产生比较大的消耗。
四个关注点在TreeMap上的答案
| 结 论 | |
|---|---|
| TreeMap是否允许键值对为空 | Key不允许为空,Value允许为空 |
| TreeMap是否允许重复数据 | Key重复会覆盖,Value允许重复 |
| TreeMap是否有序 | 按照Key的自然顺序排序或者Comparator接口指定的排序算法进行排序 |
| TreeMap是否线程安全 | 非线程安全 |
TreeMap基本数据结构
TreeMap基于红黑树实现,既然是红黑树,那么每个节点中除了Key-->Value映射之外,必然存储了红黑树节点特有的一些内容,它们是:
-
父节点引用
-
左子节点引用
-
右子节点引用
-
节点颜色
TreeMap的节点Java代码定义为:
1 static final class Entry<K,V> implements Map.Entry<K,V> {
2 K key;
3 V value;
4 Entry<K,V> left = null;
5 Entry<K,V> right = null;
6 Entry<K,V> parent;
7 boolean color = BLACK;
8 ...
9 }
由于颜色只有红色和黑色两种,因此颜色可以使用布尔类型(boolean)来表示,黑色表示为true,红色为false。
TreeMap添加数据流程总结
首先看一下TreeMap如何添加数据,测试代码为:
1 public class MapTest {
2
3
本文接下来的内容会给出插入每条数据之后红黑树的数据结构是什么样子的。首先看一下treeMap的put方法的代码实现:
1 public V put(K key, V value) {
2 Entry<K,V> t = root;
3 if (t == null) {
4 compare(key, key); // type (and possibly null) check
5
6 root = new Entry<>(key, value, null);
7 size = 1;
8 modCount++;
9 return null;
10 }
11 int cmp;
12 Entry<K,V> parent;
13 // split comparator and comparable paths
14 Comparator<? super K> cpr = comparator;
15 if (cpr != null) {
16 do {
17 parent = t;
18 cmp = cpr.compare(key, t.key);
19 if (cmp < 0)
20 t = t.left;
21 else if (cmp > 0)
22 t = t.right;
23 else
24 return t.setValue(value);
25 } while (t != null);
26 }
27 else {
28 if (key == null)
29 throw new NullPointerException();
30 Comparable<? super K> k = (Comparable<? super K>) key;
31 do {
32 parent = t;
33 cmp = k.compareTo(t.key);
34 if (cmp < 0)
35 t = t.left;
36 else if (cmp > 0)
37 t = t.right;
38 else
39 return t.setValue(value);
40 } while (t != null);
41 }
42 Entry<K,V> e = new Entry<>(key, 