算法初级面试题08——递归和动态规划的精髓阶乘汉诺塔子序列和全排列母牛问题逆序栈最小的路径和数组累加成指定整数背包问题

Posted 2021-02-08 xieyupeng

 第八课主要介绍递归和动态规划

 

 

介绍递归和动态规划

暴力递归：

1，把问题转化为规模缩小了的同类问题的子问题

2，有明确的不需要继续进行递归的条件(base case)

3，有当得到了子问题的结果之后的决策过程

4，不记录每一个子问题的解

 

动态规划

1，从暴力递归中来

2，将每一个子问题的解记录下来，避免重复计算

3，把暴力递归的过程，抽象成了状态表达

4，并且存在化简状态表达，使其更加简洁的可能

 

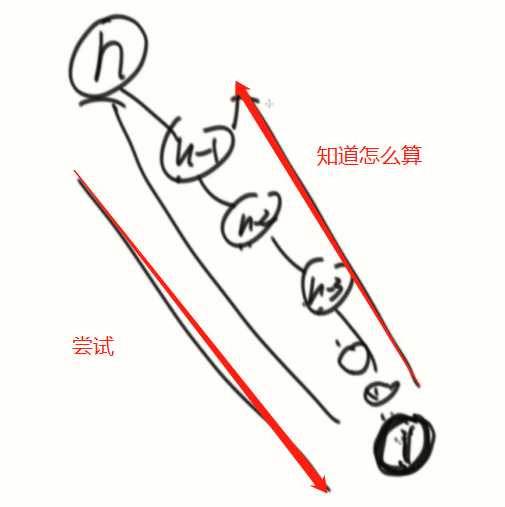
图灵引入的是：我不知道怎么算，但是我知道怎么试。知道怎么暴力破解出来。

要学会，练习懂得怎么尝试。

 

题目一

求n!的结果

循环是一个知道怎么算的过程（从1乘到n）。

递归是子问题拆分到最小问题的尝试过程。

public class Code_01_Factorial {
    public static long getFactorial1(int n) {
        if (n == 1) {
            return 1L;
        }
        return (long) n * getFactorial1(n - 1);
    }

    public static long getFactorial2(int n) {
        long result = 1L;
        for (int i = 1; i <= n; i++) {
            result *= i;
        }
        return result;
    }

    public static void main(String[] args) {
        int n = 5;
        System.out.println(getFactorial1(n));
        System.out.println(getFactorial2(n));
    }

}

 

 

 

题目二

汉诺塔问题（不能大压小，只能小压大）

打印n层汉诺塔从最左边移动到最右边的全部过程

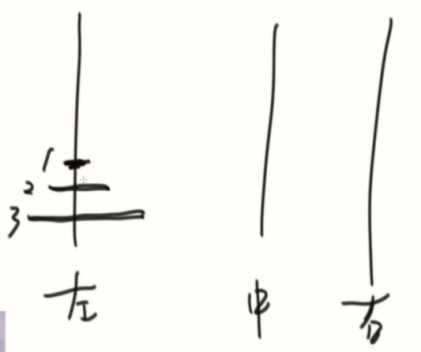
左中右另称为 from、to、help。

划分子问题

1、先把1~n-1从from移动到help

2、把单独的n移动到to

3、1~n-1从help移动到to

 

时间复杂度就是：

T(n) = T(n-1) + 1 + T(n-1) = 2T(n-1)+1（一个等比公式）

T(n-1)是移动到help

1是从from直接移动到to

T(n-1)是把全部n-1挪回去

总的步数是2的N次方减一

 

这个题目要学会尝试。
也可以写六个移动的递归，来逐一实现步骤。

 

 （该问题最基础的一个模型就是，一个竹竿上放了2个圆盘，需要先将最上面的那个移到辅助竹竿上，然后将最底下的圆盘移到目标竹竿，最后把辅助竹竿上的圆盘移回目标竹竿。）

public class Code_02_Hanoi {

    public static void hanoi(int n) {
        if (n > 0) {
            func(n, n, "left", "mid", "right");
        }
    }

    public static void func(int rest, int down, String from, String help, String to) {
        if (rest == 1) {
            System.out.println("move " + down + " from " + from + " to " + to);
        } else {
            func(rest - 1, down - 1, from, to, help);
            func(1, down, from, help, to);
            func(rest - 1, down - 1, help, from, to);
        }
    }

    //课堂上的代码
    //N 表示当前是 1~N的问题
    //一开始都在from上
    public static void process(int N, String from, String to, String help) {
        if (N == 1) {//就只有一个了，可以直接移动
            System.out.println("Move 1 from " + from + " to " + to);
        } else {//否则就是1~N的问题
            process(N - 1, from, help, to);//把1~N-1个从from移动到help
            System.out.println("Move " + N + " from " + from + " to " + to);//单独把N移动到to
            process(N - 1, help, to, from);//第三步是挪回来,把在help上的挪到to
        }
    }

    public static void moveLeftToRight(int N) {
        if (N == 1) {
            System.out.println("move 1 from left to right");
        } else {
            moveLeftToMid(N - 1);//先把N-1移动到中间
            System.out.println("move " + N + "from left to right");//把N移动到目的地
            moveMidToRight(N - 1);//再把N-1移动到目的地
        }
    }

    public static void moveRightToLeft(int N) {

    }

    public static void moveLeftToMid(int N) {
        if (N == 1) {
            System.out.println("move 1 from left to mid");
        }
        moveLeftToRight(N - 1);
        System.out.println("move " + N + "from left to mid");
        moveRightToMid(N - 1);
    }

    public static void moveMidToLeft(int N) {

    }

    public static void moveRightToMid(int N) {

    }

    public static void moveMidToRight(int N) {
        if (N == 1) {
            System.out.println("move 1 from mid to right");
        }
        moveMidToLeft(N - 1);
        System.out.println("move " + N + "from mid to right");
        moveLeftToRight(N - 1);
    }

    public static void main(String[] args) {
        int n = 3;
        hanoi(n);
    }

}

 

 

题目三

打印一个字符串的全部子序列，包括空字符串

怎么把脑里面的尝试变成code，就是写递归的能力

尝试方法：

一开始是空字符串，经过0有两个决定要a和不要a，经过1也要决定要不要b，一直尝试下去，列举所有情况。

 

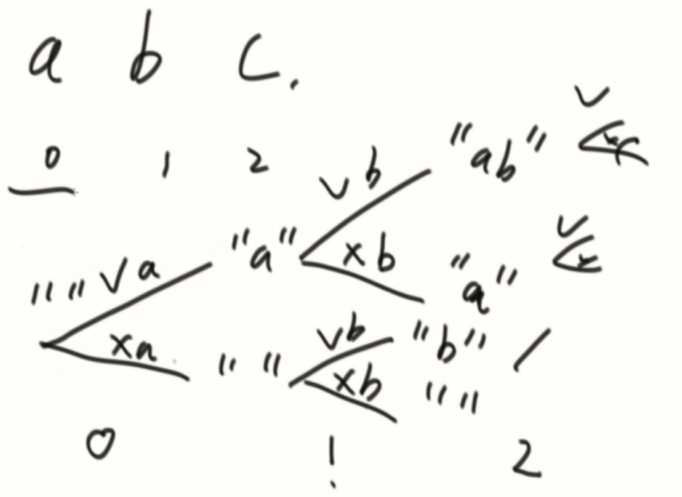
可以画一下你想尝试的图，先来个小规模的，再去写递归就没那么难写了。

 

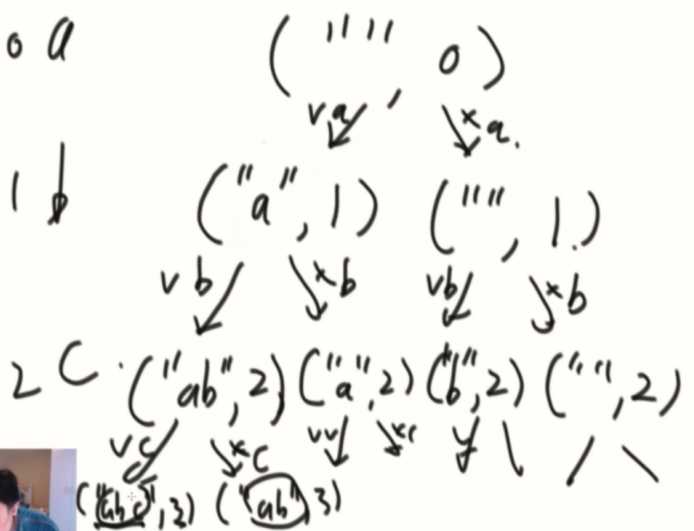
public class Code_03_Print_All_Subsquences {

    public static void printAllSubsquence(String str) {
        char[] chs = str.toCharArray();
        process(chs, 0);
    }

    public static void process(char[] chs, int i) {
        if (i == chs.length) {
            System.out.println(String.valueOf(chs));
            return;
        }
        process(chs, i + 1);
        char tmp = chs[i];
        chs[i] = 0;//用空格代替字符
        process(chs, i + 1);
        chs[i] = tmp;//直接使用字符
    }
    
//    public static void function(String str) {
//        char[] chs = str.toCharArray();
//        process(chs, 0, new ArrayList<Character>());
//    }
//
//    public static void process(char[] chs, int i, List<Character> res) {
//        if(i == chs.length) {
//            printList(res);
//        }
//        List<Character> resKeep = copyList(res);
//        resKeep.add(chs[i]);
//        process(chs, i+1, resKeep);
//        List<Character> resNoInclude = copyList(res);
//        process(chs, i+1, resNoInclude);
//    }
//
//    public static void printList(List<Character> res) {
//        // ...;
//    }
//
//    public static List<Character> copyList(List<Character> list){
//        return null;
//    }

    //课堂上的版本
    public static void printAllSub(char[] str,int i,String res){
        if (i == str.length){//到达字符串的末尾，已经没有选择了
            System.out.println(res);
            return;
        }
        printAllSub(str,i+1,res+" ");//不要当前字符的路
        printAllSub(str,i+1,res+str[i]);//要当前字符的路
    }

    public static void printAllPermutation(){

    }

    public static void main(String[] args) {
        String test = "abc";
        printAllSubsquence(test);
        printAllSub(test.toCharArray(),0,"");
    }

}

 

题目四

打印一个字符串的全部排列

 

进阶

打印一个字符串的全部排列，要求不要出现重复的排列

 

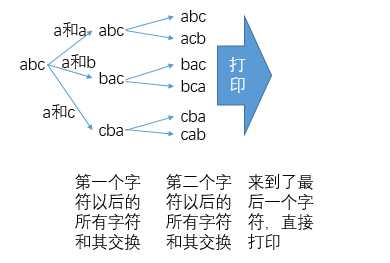
public class Code_04_Print_All_Permutations {

    public static void printAllPermutations1(String str) {
        char[] chs = str.toCharArray();
        process1(chs, 0);
    }

    public static void process1(char[] chs, int i) {
        if (i == chs.length) {
            System.out.println(String.valueOf(chs));
        }
        for (int j = i; j < chs.length; j++) {
            swap(chs, i, j);
            process1(chs, i + 1);
            swap(chs, i, j);//回溯
        }
    }

    public static void printAllPermutations2(String str) {
        char[] chs = str.toCharArray();
        process2(chs, 0);
    }

    public static void process2(char[] chs, int i) {
        if (i == chs.length) {
            System.out.println(String.valueOf(chs));
        }
        HashSet<Character> set = new HashSet<>();
        for (int j = i; j < chs.length; j++) {
            if (!set.contains(chs[j])) {
                set.add(chs[j]);
                swap(chs, i, j);
                process2(chs, i + 1);
                //swap(chs, i, j);
            }
        }
    }

    public static void swap(char[] chs, int i, int j) {
        char tmp = chs[i];
        chs[i] = chs[j];
        chs[j] = tmp;
    }

    public static void main(String[] args) {
        String test1 = "abc";
        printAllPermutations1(test1);
        System.out.println("======");
        printAllPermutations2(test1);
        System.out.println("======");

        String test2 = "acc";
        printAllPermutations1(test2);
        System.out.println("======");
        printAllPermutations2(test2);
        System.out.println("======");
    }

}

 

 

题目五

母牛每年生一只母牛，新出生的母牛成长三年后也能每年生一只母牛，假设不会死。求N年后，母牛的数量。

一遇到这种递推的题目，不知道怎么试，先列出前几项，递推是有高度结构化的解的。

 

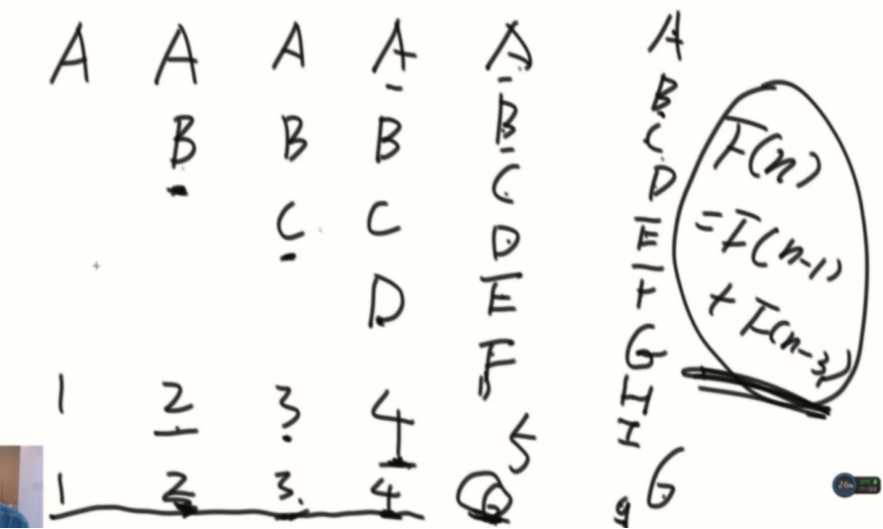
然后要想为什么？

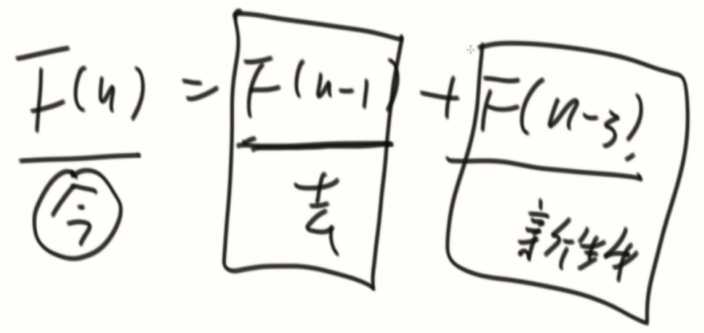
F(n) = F(n-1) + F(n-3)

因为牛都不会死，所以会有去年的牛F(n-1),三年前牛的数量，此时都可以生小牛，所以会有F(n-3)这部分。

 

public class Code_05_Cow {

    public static int cowNumber1(int n) {
        if (n < 1) {
            return 0;
        }
        if (n == 1 || n == 2 || n == 3) {
            return n;
        }
        return cowNumber1(n - 1) + cowNumber1(n - 3);
    }

    //非递归版本
    public static int cowNumber2(int n) {
        if (n < 1) {
            return 0;
        }
        if (n == 1 || n == 2 || n == 3) {
            return n;
        }
        int res = 3;
        int pre = 2;
        int prepre = 1;
        int tmp1 = 0;
        int tmp2 = 0;
        for (int i = 4; i <= n; i++) {
            tmp1 = res;
            tmp2 = pre;
            res = res + prepre;
            pre = tmp1;
            prepre = tmp2;
        }
        return res;
    }

    public static void main(String[] args) {
        int n = 20;
        System.out.println(cowNumber1(n));
        System.out.println(cowNumber2(n));
    }

}

 

进阶

如果每只母牛只能活10年，求N年后，母牛的数量。

 

题目六

给你一个栈，请你逆序这个栈，不能申请额外的数据结构，只能使用递归函数。如何实现？

 

本题考查栈的操作和递归函数的设计，我们需要设计出两个递归函数。

 

递归函数一：将栈stack 的栈底元素返回并移除。

具体过程就是如下代码中的getAndRemoveLastElement 方法。

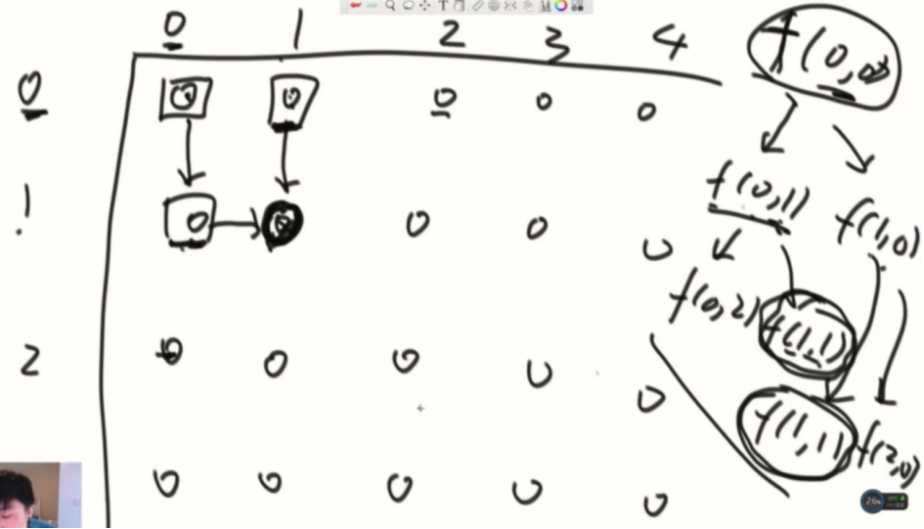
如果从stack 的栈顶到栈底依次为3、2、1，这个函数的具体过程如下图所示。

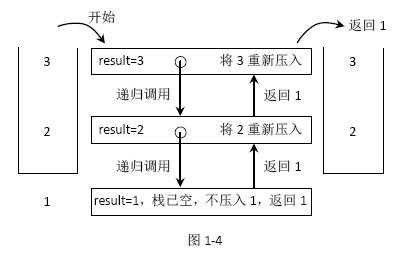
递归函数二：逆序一个栈，就是题目要求实现的方法，具体过程就是如下代码中的reverse方法。该方法使用了上面提到的getAndRemoveLastElement 方法。

如果从stack 的栈顶到栈底依次为3、2、1，reverse 函数的具体过程如图1-5 所示。

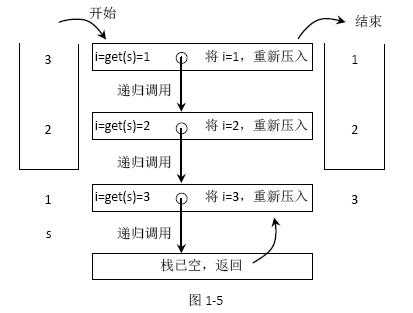
getAndRemoveLastElement 方法在图中简单表示为get 方法，表示移除并返回当前栈底元素。

public class Code_06_ReverseStackUsingRecursive {

    /**
     * 以1，2，3为例，从栈顶到栈底依次为3，2，1
     */
    public static void reverse(Stack<Integer> stack) {
        if (stack.isEmpty()) {
            return;
        }
        int i = getAndRemoveLastElement(stack);//得到栈底元素
        reverse(stack);//递归，所以i依次为1，2，3
        stack.push(i);//回溯，依次压入3，2，1
    }

    //得到栈底元素并它移除，并且其它元素压回栈
    public static int getAndRemoveLastElement(Stack<Integer> stack) {
        int result = stack.pop();
        if (stack.isEmpty()) {
            return result;
        } else {
            int last = getAndRemoveLastElement(stack);
            stack.push(result);//回溯，将其它元素重新压回栈
            return last;//返回栈底元素
        }
    }

    public static void main(String[] args) {
        Stack<Integer> test = new Stack<Integer>();
        test.push(1);
        test.push(2);
        test.push(3);
        test.push(4);
        test.push(5);
        reverse(test);
        while (!test.isEmpty()) {
            System.out.println(test.pop());
        }

    }

}

 

题目七

给你一个二维数组，二维数组中的每个数都是正数，要求从左上角走到右下角，每一步只能向右或者向下。沿途经过的数字要累加起来。返回最小的路径和。

 

没见过的动态规划有一个统一的套路，写出递归版本尝试版本后，得出来的动态规划的方法是高度套路的。

所有动态规划都是由暴力版本优化来的。

 

 

问题划分为了：向下或者向右的结果，从中选最小的路径，就是最后的答案。

    //课堂上的代码
    public static int walk(int[][] matrix, int i, int j) {
        int x = matrix.length - 1;
        int y = matrix[0].length - 1;
        if (i == x && j == y) {
            return matrix[i][j];
        }
        if (i == x)//如果i到达行底部，只能向右走。
            return matrix[i][j] + walk(matrix, i, j + 1);

        if (j == y)//如果j到达列边界，只能向下走。
            return matrix[i][j] + walk(matrix, i + 1, j);
        //其他情况，需要对向下和向右进行对比，选出最优解
        int right = walk(matrix, i, j + 1);
        int down = walk(matrix, i + 1, j);
        return matrix[i][j] + Math.min(right, down);

    }

 

暴力枚举有待优化：有大量的重复解产生，很多部分都重复计算。

把重复计算的部分缓存起来，重复的时候直接调用就能省时间。

 

什么样的尝试版本递归可以改成动态规划？

当把递归过程展开，发现有重复的状态，与到达它的路径是没有关系的，那么它一定能改成动态规划（无后效性问题）。

有后效性的是，汉罗塔、N皇后问题（前面的举动会影响后面的结果）。

 

 

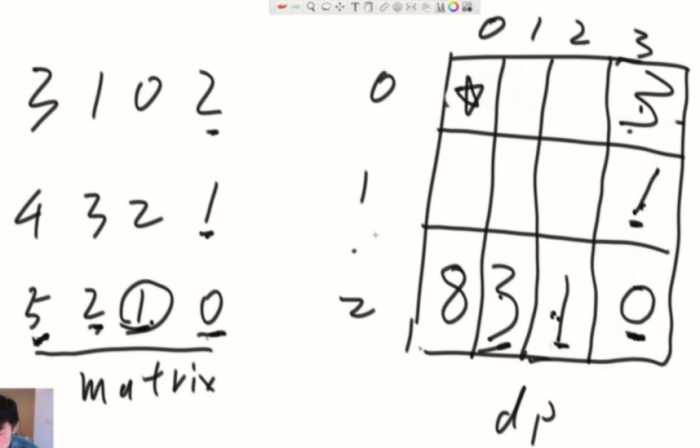
准备一个dp表

1、把需要的位置点出来

2、回到base case中把不被依赖的位置设置好（这题是最后一行/列），然后分析普遍位置是怎么依赖的（需要哪些位置的帮助），反过去就是整个计算顺序。 依次计算，推到顶部就是答案。

 

 

类似一个搭积木的过程，堆积到一定条件就能出现答案。

public class Code_07_MinPath {

    public static int minPath1(int[][] matrix) {
        return process1(matrix, matrix.length - 1, matrix[0].length - 1);
    }

    //从{i,j}出发，到达最右下角位置，最小路径和是多少？
    public static int process1(int[][] matrix, int i, int j) {
        int res = matrix[i][j];
        if (i == 0 && j == 0) {
            return res;
        }
        if (i == 0 && j != 0) {
            return res + process1(matrix, i, j - 1);
        }
        if (i != 0 && j == 0) {
            return res + process1(matrix, i - 1, j);
        }
        return res + Math.min(process1(matrix, i, j - 1), process1(matrix, i - 1, j));
    }
    
    //动态规划
    public static int minPath2(int[][] m) {
        if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
            return 0;
        }
        int row = m.length;
        int col = m[0].length;
        int[][] dp = new int[row][col];
        dp[0][0] = m[0][0];
        //第一列赋值
        for (int i = 1; i < row; i++) {
            dp[i][0] = dp[i - 1][0] + m[i][0];
        }
        //第一行赋值
        for (int j = 1; j < col; j++) {
            dp[0][j] = dp[0][j - 1] + m[0][j];
        }
        //最优赋值
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + m[i][j];
            }
        }
        return dp[row - 1][col - 1];
    }

    // for test
    public static int[][] generateRandomMatrix(int rowSize, int colSize) {
        if (rowSize < 0 || colSize < 0) {
            return null;
        }
        int[][] result = new int[rowSize][colSize];
        for (int i = 0; i != result.length; i++) {
            for (int j = 0; j != result[0].length; j++) {
                result[i][j] = (int) (Math.random() * 10);
            }
        }
        return result;
    }

    //课堂上的代码
    public static int walk(int[][] matrix, int i, int j) {
        int x = matrix.length - 1;
        int y = matrix[0].length - 1;
        if (i == x && j == y) {
            return matrix[i][j];
        }
        if (i == x)//如果i到达行底部，只能向右走。
            return matrix[i][j] + walk(matrix, i, j + 1);

        if (j == y)//如果j到达列边界，只能向下走。
            return matrix[i][j] + walk(matrix, i + 1, j);
        //其他情况，需要对向下和向右进行对比，选出最优解
        int right = walk(matrix, i, j + 1);
        int down = walk(matrix, i + 1, j);
        return matrix[i][j] + Math.min(right, down);

    }


    public static void main(String[] args) {
        int[][] m = {{1, 3, 5, 9}, {8, 1, 3, 4}, {5, 0, 6, 1}, {8, 8, 4, 0}};
        System.out.println(minPath1(m));
        System.out.println(minPath2(m));

        m = generateRandomMatrix(6, 7);
        System.out.println(minPath1(m));
        System.out.println(minPath2(m));
    }
}

 

题目八

给你一个数组arr，和一个整数aim。如果可以任意选择arr中的数字，能不能累加得到aim，返回true或者false

 

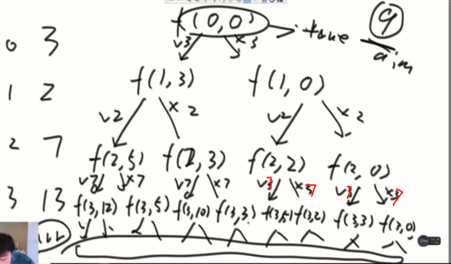
这是一个无后效性问题。可以使用dp，不管之前做了什么选择，只要是之前的累加和、步数是固定的，返回值一定确定。

 

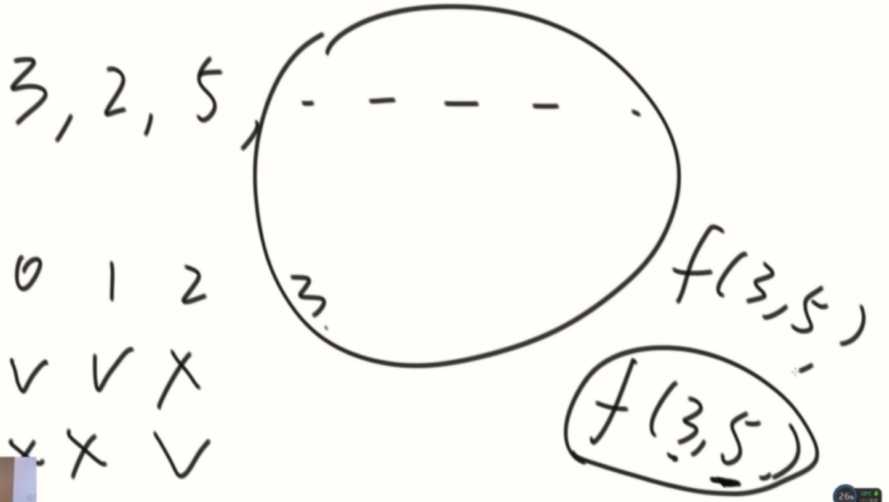
i就是数组长度，sum的范围是全部数的和。

 

 

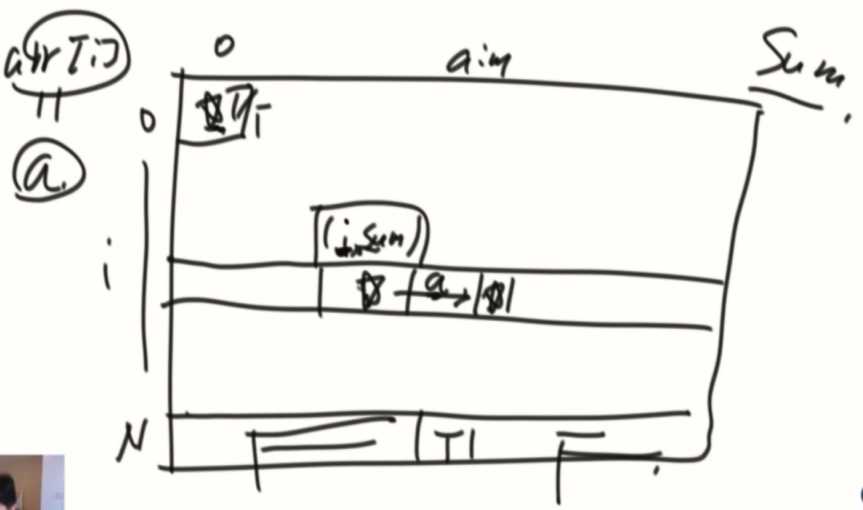
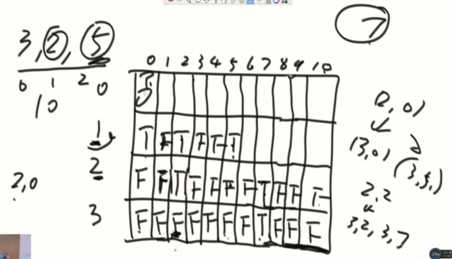
首先查看递归的base case，分析出最后一行，只有aim对应的列是T其余全是F，通过查看递归的规律，普遍的位置依赖的是两种情况，[i+1,sum]和[i+1,sum+arr[i]]，逐个计算把整个dp数组填满。如果aim超出sum，那肯定是计算不出来的，因为sum是数组全部数加起来的和。

最后计算出[0,0]的位置，可以直接返回。

和题意没关系了。（从暴力递归中总结出来）

 

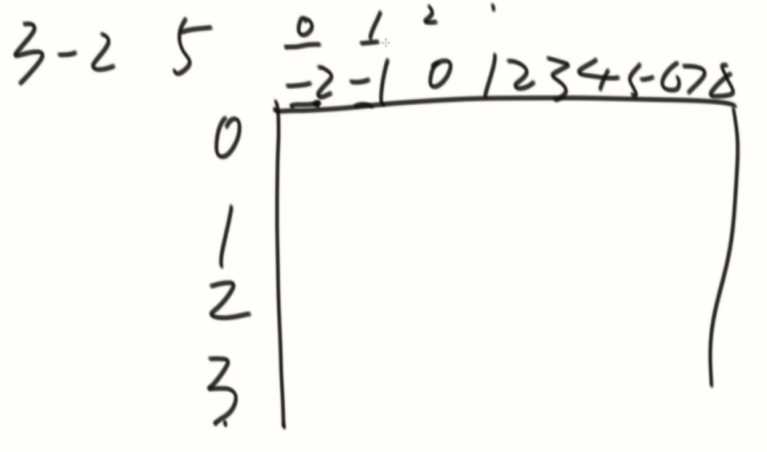
有负数怎么办？要设计一下

 

public class Code_08_Money_Problem {

    public static boolean money1(int[] arr, int aim) {
        return process1(arr, 0, 0, aim);
    }

    public static boolean process1(int[] arr, int i, int sum, int aim) {
        if (sum == aim)
            return true;

        // sum != aim
        if (i == arr.length)
            return false;

        return process1(arr, i + 1, sum, aim) || process1(arr, i + 1, sum + arr[i], aim);
    }

    public static boolean money2(int[] arr, int aim) {
        boolean[][] dp = new boolean[arr.length + 1][aim + 1];
        for (int i = 0; i < dp.length; i++) {
            dp[i][aim] = true;//以目标金额为列的肯定为true
        }
        for (int i = arr.length - 1; i >= 0; i--) {//从最后一行开始
            for (int j = aim - 1; j >= 0; j--) {//aim往后的都超过，没必要看
                dp[i][j] = dp[i + 1][j];//通过直接的下方的判断。
                if (j + arr[i] <= aim) {//如果该数加上arr[i](当前可以累加的数)少于等于目标数。
                    // 有可能可行，通过查看加上了arr[i](当前可以累加的数)的状态来判断
                    dp[i][j] = dp[i][j] || dp[i + 1][j + arr[i]];
                }
            }
        }
        return dp[0][0];
    }

    public static boolean check(int[] arr,int i,int sum,int aim){
        if (i == arr.length){//判断是否走到最后一步
            return sum == aim;
        }
        return check(arr,i+1,sum,aim) || check(arr,i+1,sum+arr[i],aim);
    }



    public static void main(String[] args) {
        int[] arr = { 1, 4, 8 };
        int aim = 12;
//        System.out.println(money1(arr, aim));
//        System.out.println(money2(arr, aim));

        System.out.println(check(arr,0,0,aim));

    }

}

 

题目九

给定两个数组w和v，两个数组长度相等，w[i]表示第i件商品的重量，v[i]表示第i件商品的价值。 再给定一个整数bag，要求你挑选商品的重量加起来一定不能超过bag，返回满足这个条件下，你能获得的最大价值。

 

public class Code_09_Knapsack {

    public static int maxValue1(int[] c, int[] p, int bag) {
        return process1(c, p, 0, 0, bag);
    }

    public static int process1(int[] weights, int[] values, int i, int alreadyweight, int bag) {
        if (alreadyweight > bag) {
            return 0;
        }
        if (i == weights.length) {
            return 0;
        }
        //每次就两种情况：1、不拿商品 2、拿商品承担重量
        return Math.max(
                process1(weights, values, i + 1, alreadyweight, bag),
                values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag));
    }
    //carat 克拉/重量  price 价值
    public static int maxValue2(int[] c, int[] p, int bag) {
        int[][] dp = new int[c.length + 1][bag + 1];
        for (int i = c.length - 1; i >= 0; i--) {
            for (int j = bag; j >= 0; j--) {//超过bag将毫无意义
                dp[i][j] = dp[i + 1][j];
                if (j + c[i] <= bag) {
                    dp[i][j] = Math.max(dp[i][j], p[i] + dp[i + 1][j + c[i]]);
                }
            }
        }
        return dp[0][0];
    }

    public static void main(String[] args) {
        int[] c = { 3, 2, 4, 7 };
        int[] p = { 5, 6, 3, 19 };
        int bag = 11;
        System.out.println(maxValue1(c, p, bag));
        System.out.println(maxValue2(c, p, bag));
    }

}