最小生成树算法

Posted 2021-02-08 fsmly

最小生成树的形成
　　(1)一个贪心策略设计如下
       每个时刻生长最小生成树的一条边，并在整个策略的实施过程中，遵守下述循环不变式的边集合A：
         
　　每一步，选择一条边(u,v)加入集合A，使得A不违反循环不变式。
　　这样的边使得我们可以“安全地”将之加入到集合A而不会破坏A的循环不变式，因此称之为集合A的“安全边”。
　　

　　(2)使用的循环不变式方式如下：
　　初始化：集合A直接满足循环不变式。
　　保持：算法的循环通过只加入安全边来维持循环不变式。
　　终止：所有加入到集合A中的边都属于某棵最小生成树，因此，算法第5行所返回的集合A必然是一棵最小生成树。
　　说明：循环不变式告诉了我们存在一棵生成树，满足。在进入while循环时，A是T的真子集，因此必然存在一条边，使得，并且(u,v)对于集合A是安全的。
　　(3)定义一些概念

　　
　　切割：无向图G=(V,E)的一个切割(S,V-S)是集合V的一个划分。

　　横跨切割：如果一条边(u,v)∈E的一个端点在集合S中，另一个端点在集合V-S中，则称该条边横跨切割(S,V-S)。

　　尊重集合：如果集合A中不存在横跨该切割的边，则称该切割尊重集合A。

　　轻量级边：在横跨一个切割的所有边中，权重最小的边称为轻量级边

　　(4)距离说明上述概念

　　

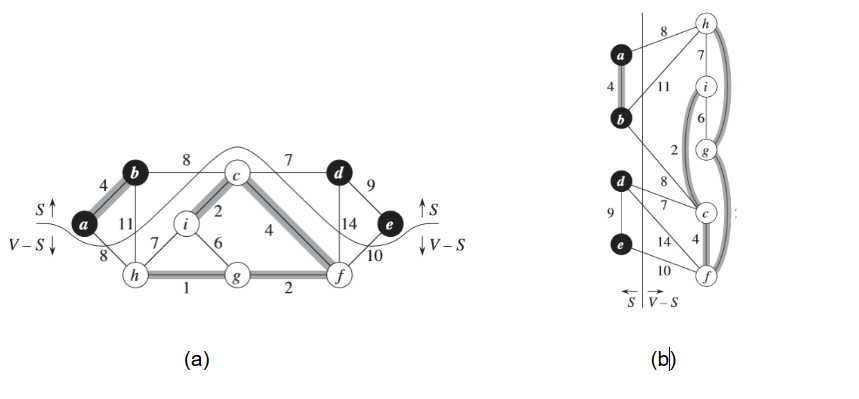
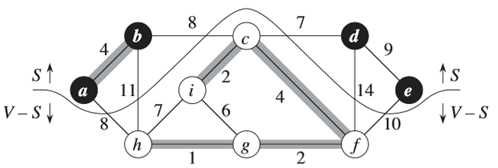
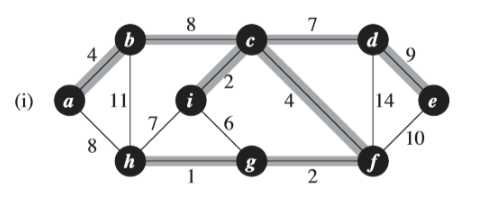
　　图(a)中所示的黑色结点位于集合S中，白色结点位于V-S中。横跨该切割的边是那些连接白色结点和黑色结点的边。如<a,h><b,c><c,d>等等，其中<d,c>是轻量级边。若定义加了阴影的边属于集合A，那么可以看出集合A中没有横跨切割的边，所以切割<S,V-S>尊重集合A。

　　图(b)中是同样一个图，只是换了视角。

　　(5)辨认安全边的规则

　　设G=(V,E)是一个在边E上定义了实数值权重函数ω的连通无向图。设集合A为E的一个子集，且A包含在图G的某棵最小生成树中，设(S,V-S)是图G中尊重集合A的任意一个切割，

又设(u,v)是横跨切割(S,V-S)的一条轻量级边。那么边(u,v)对于集合A是安全的。

　　证明：

　　

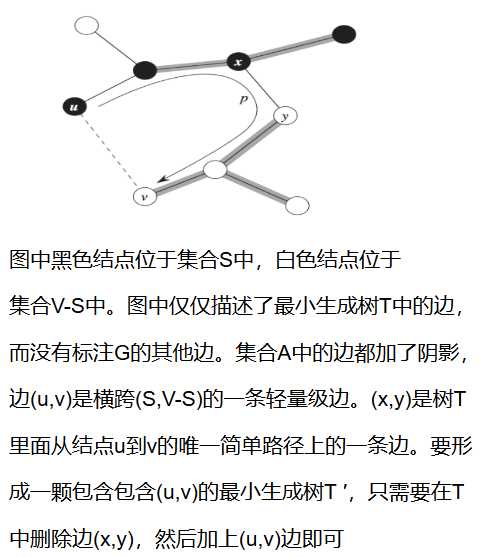
　　我们现在构建一个最小生成树T ′，通过将A∪{(u,v)}包括在树T ‘中，从而证明(u,v)对集合A来说是安全的。T中包含有G的所有结点，所以(u,v)与T中从结点u到结点v的简单路径p形成一个环。如上图所示。由于结点u，v分别处于切割S，V-S中，T中至少含有一条简单路径p并且横跨该切割。假设(x,y)是这样一条边。由于切割(S,V-S)尊重集合A，所以(x,y)不在集合A中。又因为（x，y）位于T中从u到v的唯一一条简单路径上，将这条边删除会导致T被分为两个连通分量，这时候，将（u，v）加入就能将这两个连通分量连接起来成为一颗心得生成树。

　　这时候我们来证明T ′是一颗最小生成树。

　　由于（u，v）是横跨切割的一条轻量级边，并且边（x，y）也横跨该切割，所以我们有ω(u,v)≤ ω(x,y)，所以可以简单得出这样一个关系

　　　　

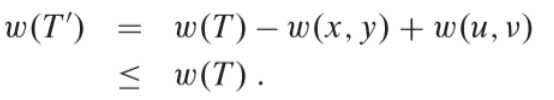
　　又因为T是一颗最小生成树，ω(T) ≤ ω(T ‘)，因此T ′也是一颗最小生成树。

　　因为 A∈T，且 （x，y）?A，所以A∈T ‘ 。因此。由于T ‘ 是最小生成树，(u,v)对于集合A而言是安全的。

　　在算法GENERIC-MST推进的过程中，集合A始终保持无环状态( 每条边都是安全的 )。算法执行的任意时刻，图G A =(V,A)是一个森林。

　　while循环执行|V|-1次，每次找出构造最小生成树所需的一条边。每遍循环将树的数量减少1。当整个森林只含有一棵树时，算法终止。

Kruskal算法
　　Kruskal和Prim算法是求解最小生成树的两个经典算法。它们都是GENERIC-MST算法的具体细化：

　　(1)Kruskal算法找安全边的方法：在所有连接森林中两棵不同树的边中，找权重最小的边(u,v)。设C 1 和C 2 为边(u,v)所连接的两棵树。边(u,v)是C 1 的一条安全边。

　　

　　(2)简单讲述一下Kruskal算法的工作过程。算法的1~3行将集合A初始化为一个空集，并创建|V|棵树，每棵树仅包含一个结点，作为初始情况。5~8行中的for循环按照权重从低到高的次序对每一条边逐一进行检查。对于每条边(u,v)而言，循环将检查该结点u和结点v是否属于同一棵树。如果是，这条边不能加入，避免形成环路。如果不是，则两个端点分别属于不同的树，算法第7行将吧这些边加入到集合A中，第8行将两棵树进行合并。

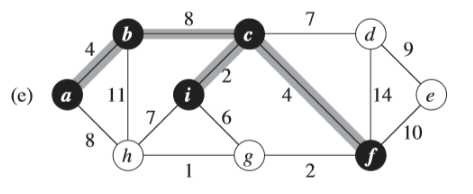
　　(3)下面给出一个具体的例子看看算法的流程

　　①首先找到最小权重的边为<h,g> = 1

　　

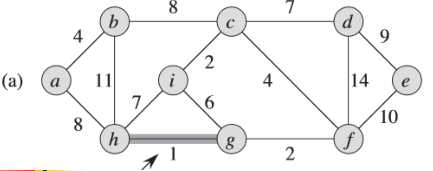
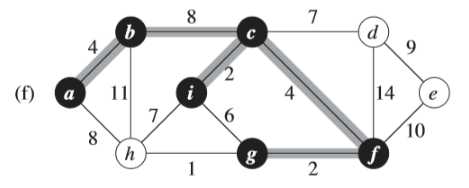
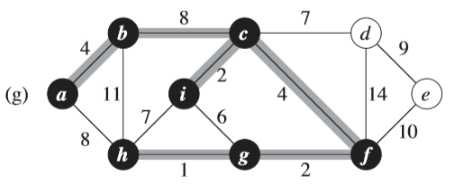
 　　②继续寻找下一条权重次小的边，以此类推

　　

　　

　　

　　

 

　　

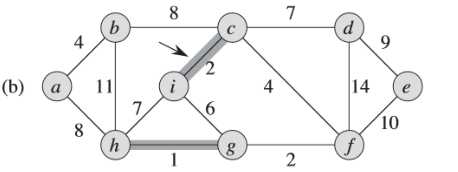
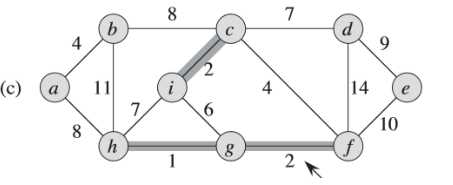
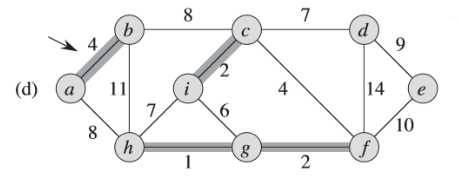
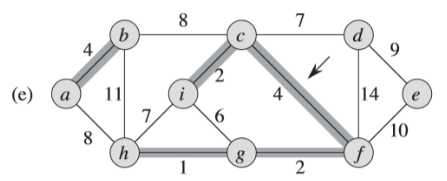
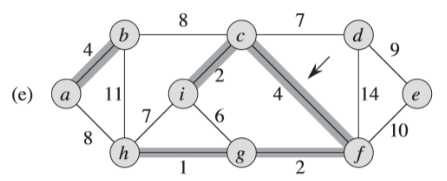
　　③注意到，(f)图中此时权重为6的边的两个端点i和g都属于同一棵树(<i,c,f,g,h>)中，所以不能加这条边加入，否则会形成环路

　　

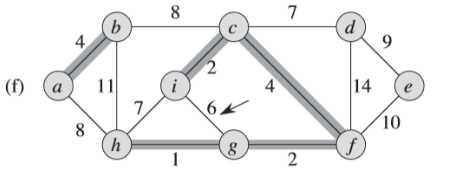
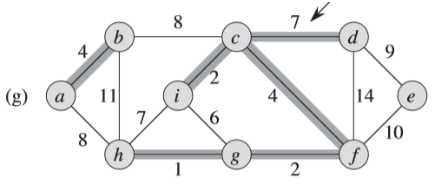
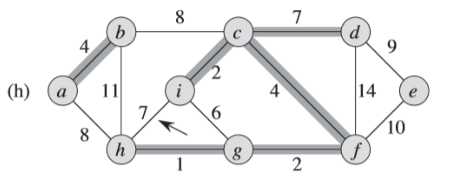
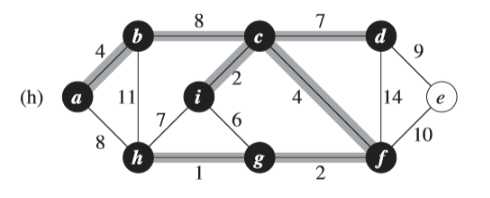
　　④同③一样，（h）图中的权重为7的边不同加入集合中，避免形成环路(<i,c,f,g,h>)

　　

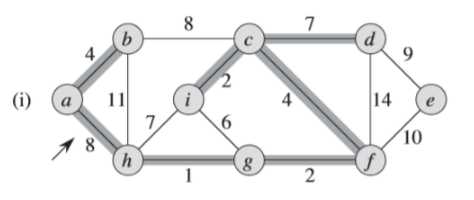
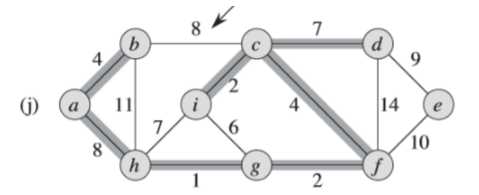
　　⑤同④一样，（j）图中的权重为8的边不同加入集合中，避免形成环路(<a,b,d,c,f,g,h>)

　　

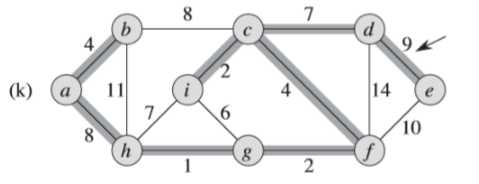
　　⑥同理，<e,f>边如果加入集合中，会形成环路<c,d,e,f>；<b,h>不能加入集合中，会形成<a,b,h>环路；<d,f>不能加入集合中，会形成<c,f,d>环路

　　

　　

　　

Prim算法

　　(1)Prim算法的每一步是在连接集合A和A之外的结点的所有边中，选择一条轻量级边加入到A中。所加入的边对于A也是安全的。Prim算法的基本性质：集合A中的边总是构成一棵树。

　　

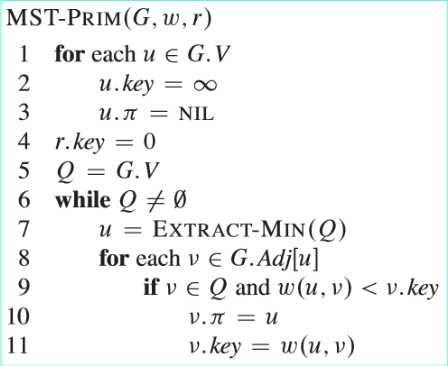
 　　(2)简单描述一下上述算法的流程。1~5行将每个节点的key值设置为∞（除根节点r以外，根节点key值置为0，作为第一个被处理的点），然后将每个结点的父节点置为NIL，并对最小优先队列Q进行初始化，使其包含图中的所有节点。

　　算法维持的循环不变式由3个部分组成：

　　①A={(v,v.π):v∈V-{r}-Q}

　　②已经加入到最小生成树中的结点集合为V-Q

　　③对于所有结点v∈Q，如果v.π≠NIL，则v.key<∞并且v.key是连接结点v和最小生成树中某个节点的轻量级边(v,v.π)的权重

　　第7行找出结点v∈Q，该结点是某条横跨切割<V-Q,Q>的轻量级边的一个端点，然后将结点u从队列中删除，并将其加入到集合V-Q中，也就是将边<u,u.π>加入到集合A中。8~11行的for循环将每个与u邻接但是不在树中的结点v的key和π属性进行更新，从而维持循环不变式。

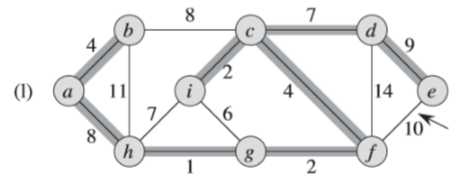
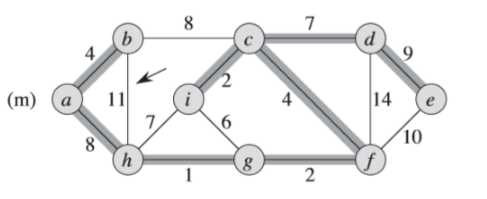
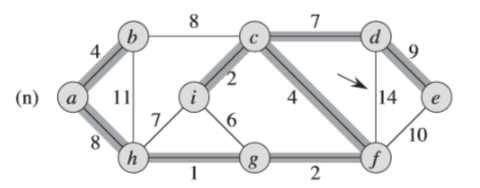
　　(3)简单看一个Prim算法的例子

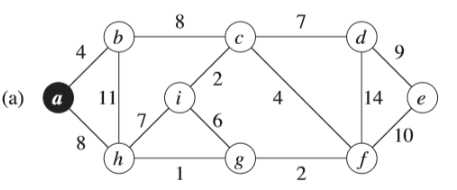
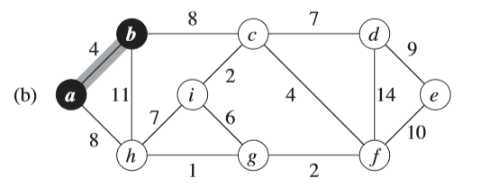
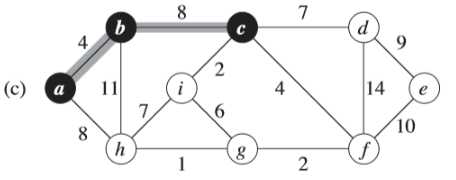
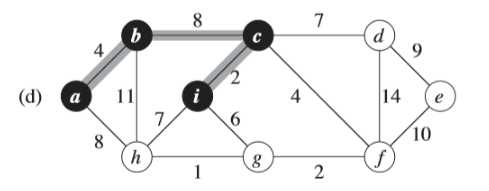
　　例子中，初始的根节点为a，加阴影的边和黑色结点属于树A。在算法的每一步，树中的结点就决定了图的一个切割，横跨该切割的一条轻量级边就被加入到树中。

　　例如：在图(b)，轻量级边有两条，<b,c>,<a,h>的权重都为8，所以可以选择两条边中的一条加入到树中