算法初级面试题07——前缀树应用介绍和证明贪心策略拼接字符串得到最低字典序切金条问题项目收益最大化问题随时取中位数宣讲会安排

Posted 2021-02-07 xieyupeng

第六课主要介绍图，不经常考，故今天先讲第七课的内容，介绍比较常考的树和贪心算法

 

介绍前缀树

何为前缀树？ 如何生成前缀树？

 

 

 

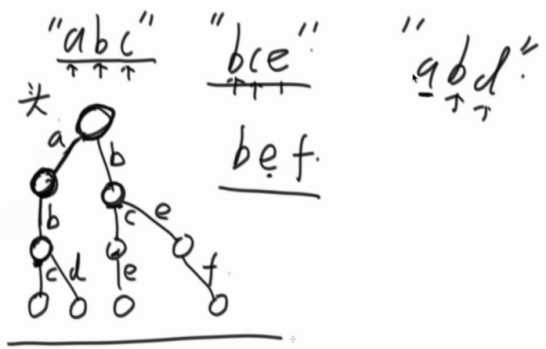
可以查有多少个字符串以“be”为前缀。

如果要判断有没有“be”这个节点，每个节点上加上一个数据项，有多少个字符串以当前节点结尾的（可以查加了多少次特定字符串）。

 

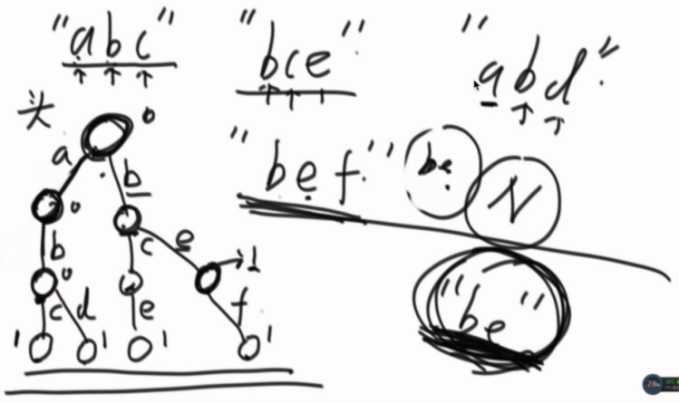
给一个字符串、返回多少个字符串以这个为前缀。

再加一个数据项，记录该节点被划过多少次。

 

大概实现：

 

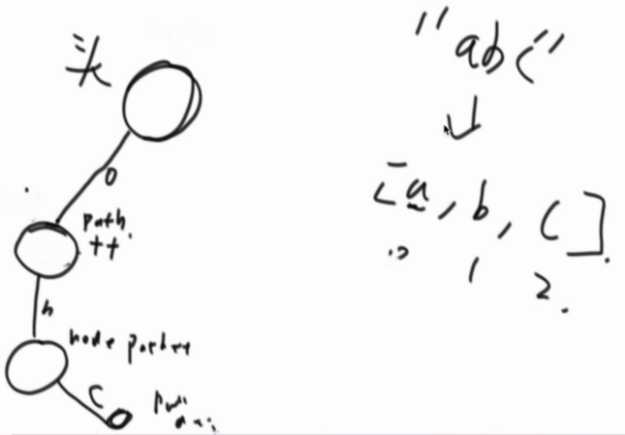
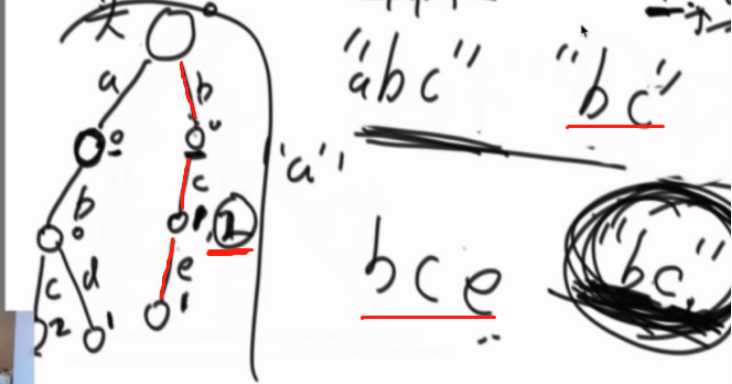
删除逻辑：

根据path是否变为0，来判断是否继续往下删。

 

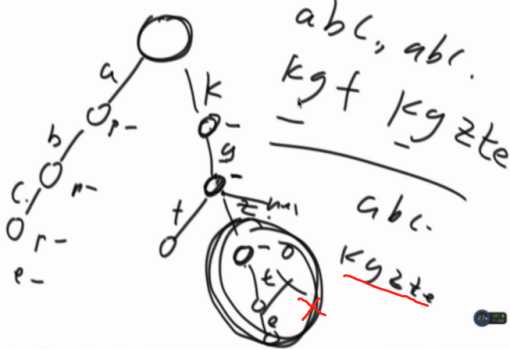
可以解决以下问题：

一个字符串类型的数组arr1，另一个字符串类型的数组arr2。

arr2中有哪些字符，是arr1中出现的？请打印

arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印

arr2中有哪些字符，是作为arr1中某个字符串前缀出现的？请打印arr2中出现次数最大的前缀。

public class Code_01_TrieTree {

    public static class TrieNode {
        public int path;//多少个到达过节点
        public int end;//多少个以这个节点结尾
        public TrieNode[] nexts;//表示下一个节点的情况

        public TrieNode() {
            path = 0;
            end = 0;
            //26个字母
            nexts = new TrieNode[26];
        }
    }

    public static class Trie {
        private TrieNode root;

        public Trie() {
            root = new TrieNode();
        }

        public void insert(String word) {
            if (word == null) {
                return;
            }
            char[] chs = word.toCharArray();
            TrieNode node = root;
            int index = 0;
            for (int i = 0; i < chs.length; i++) {
                index = chs[i] - ‘a‘;//a index 0 -- b index 1 -- ...字母对应的
                if (node.nexts[index] == null) {//没有路就新建出来
                    node.nexts[index] = new TrieNode();
                }
                node = node.nexts[index];
                node.path++;
            }
            node.end++;
        }

        public void delete(String word) {
            if (search(word) != 0) {
                char[] chs = word.toCharArray();
                TrieNode node = root;
                int index = 0;
                for (int i = 0; i < chs.length; i++) {
                    index = chs[i] - ‘a‘;
                    if (--node.nexts[index].path == 0) {
                        node.nexts[index] = null;
                        return;
                    }
                    node = node.nexts[index];
                }
                node.end--;
            }
        }

        public int search(String word) {
            if (word == null) {
                return 0;
            }
            char[] chs = word.toCharArray();
            TrieNode node = root;
            int index = 0;
            for (int i = 0; i < chs.length; i++) {
                index = chs[i] - ‘a‘;
                if (node.nexts[index] == null) {
                    return 0;
                }
                node = node.nexts[index];
            }
            return node.end;
        }

        public int prefixNumber(String pre) {
            if (pre == null) {
                return 0;
            }
            char[] chs = pre.toCharArray();
            TrieNode node = root;
            int index = 0;
            for (int i = 0; i < chs.length; i++) {
                index = chs[i] - ‘a‘;
                if (node.nexts[index] == null) {
                    return 0;
                }
                node = node.nexts[index];
            }
            return node.path;
        }
    }

    public static void main(String[] args) {
        Trie trie = new Trie();
        System.out.println(trie.search("zuo"));
        trie.insert("zuo");
        System.out.println(trie.search("zuo"));
        trie.delete("zuo");
        System.out.println(trie.search("zuo"));
        trie.insert("zuo");
        trie.insert("zuo");
        trie.delete("zuo");
        System.out.println(trie.search("zuo"));
        trie.delete("zuo");
        System.out.println(trie.search("zuo"));
        trie.insert("zuoa");
        trie.insert("zuoac");
        trie.insert("zuoab");
        trie.insert("zuoad");
        trie.delete("zuoa");
        System.out.println(trie.search("zuoa"));
        System.out.println(trie.prefixNumber("zuo"));

    }

}

 

 

贪心策略

贪心策略正确性的证明，千万不要纠结，因为纠结你能死去。

 

想练贪心，记贪心的点就够了，写对数器的方式来验证。

 

不用去纠结哪个策略，证明上哪个是对的。这是一个大套路。

 

字典序介绍

例如abc和bce对比，想象成26进制的数进行对比。

长度不等的时候，把短的后面扩长来对比，后补最小的单位。

 

 

 

题目：给定一个字符串类型的数组strs，找到一种拼接方式，使得把所有字符串拼起来之后形成的字符串具有最低的字典序。

 

 

 

什么叫做贪心？

定义一个指标，在这个指标下，把每一个样本分出一个优先来，按照优先大的先执行，优先小的后执行，这就是贪心。

贪心就是一件事情，贪心就是某一种简洁的标准，在这个标准下把所有东西分出个一二三来，然后根据这个优先级，决定一种顺序，就是贪心。

 

贪心案例：

贪心就是找距离目标最近的拿，不管最终的结果，只注重局部或者眼前的结果的方法

按照这种方法就是有可能丧失全局最优的

 

就好比两个人分5个大饼，一次可以拿一个或者两个，不吃完不允许再拿

A：用贪心方法：第一次拿两个，B拿一个，那么B最终拿3个

这个就是贪心方法失败的一个例子

 

有的时候贪心算法也是可以得到最优解的,比如还是大饼的例子，但是现在总数是7个了

A继续贪心，先两个，再两个就是4个了；

而B先1个，后2个，就只能是3个

 

介绍完贪心就回到题目：

如果对数组进行排序，再拼接一起，那是不行的。

 

 

 

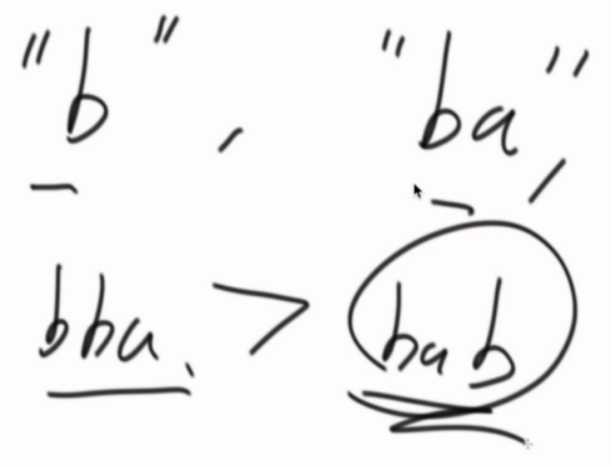
正确的排序策略：

str1做前缀str2跟后面。和相反着对比。（每个字符串作为前缀贴在一起比较）

 

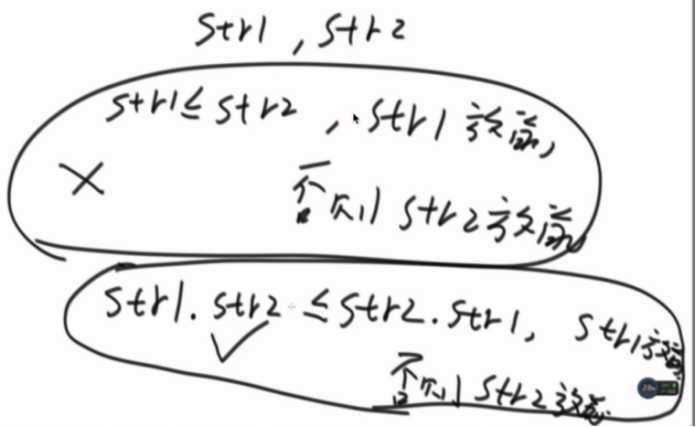
排序策略不成立的例子。

比较策略没有传递性，是一个环。

 

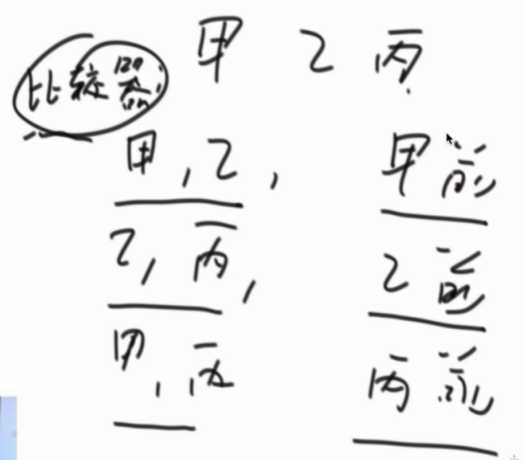
有传递性是：

 

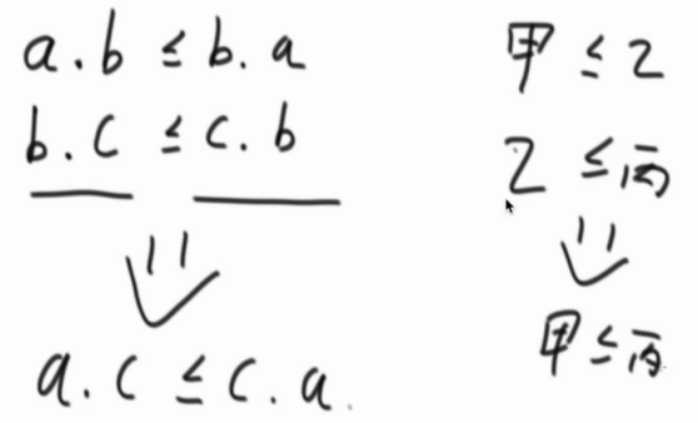
这个题比较策略就是贪心策略。要确定的一件事情，排序策略是有传递性的。

 

把a.b看做成K进制的数，“abc” “efg” abcefg，其实就是abc向左移动了b这个数的长度位，再加入efg。

 

 

 

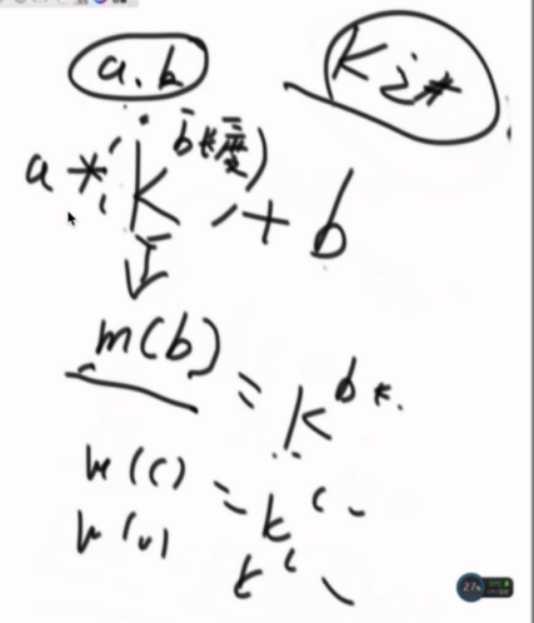
等式两边减b乘c，第二个式子减b乘a

然后再化简。

 

展开后ac抹掉，同时除与b，a移过去右，c移过去左...

 

证明排序策略是有传递性，是一个对的排序：

 

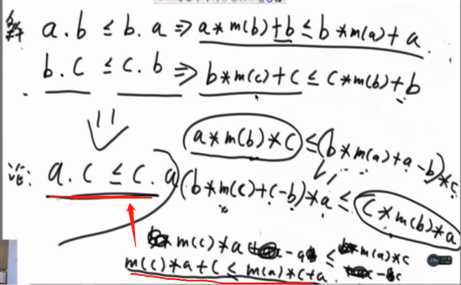
还要证明用这种排序策略得到的序列，就是字典序最小的。

先证明一件事情，序列里面任意调换两个字符串的顺序后，都会产生更大的字典序。

由于传递性：a.m1<=m1.a

 

 

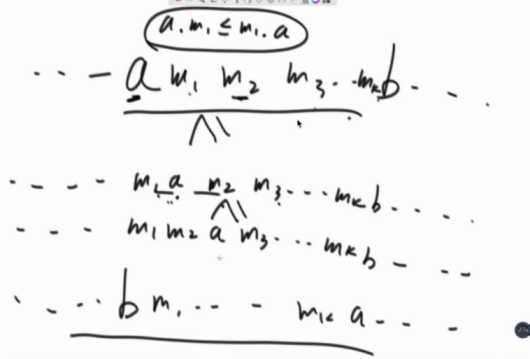
一路下去，然后紧贴着b，b再和a交换。一路下来都是大于等于，那么肯定就只有比原始序列大。（所以原始序列是最经济的）

 

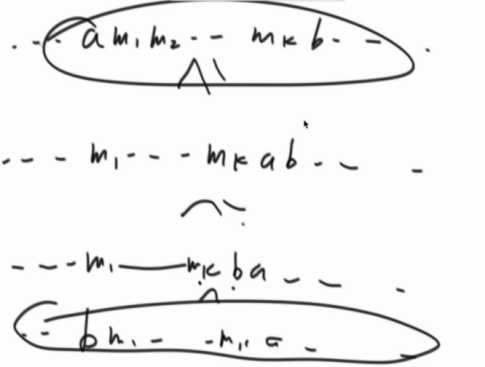
这是一个贪心策略从提出策略，到证明正确，要付出较大的心血。

所以用对数器来验证他对不对即可。

题目实现代码：

 

public class Code_05_LowestLexicography {

    public static class MyComparator implements Comparator<String> {
        @Override
        public int compare(String a, String b) {
            return (a + b).compareTo(b + a);
        }
    }

    public static String lowestString(String[] strs) {
        if (strs == null || strs.length == 0) {
            return "";
        }
        //按照对比器排序
        Arrays.sort(strs, new MyComparator());
        String res = "";
        for (int i = 0; i < strs.length; i++) {
            res += strs[i];
        }
        return res;
    }

    public static void main(String[] args) {
        String[] strs1 = { "jibw", "ji", "jp", "bw", "jibw" };
        System.out.println(lowestString(strs1));

        String[] strs2 = { "ba", "b" };
        System.out.println(lowestString(strs2));

    }

}

 

 

 

 

题目：

一块金条切成两半，是需要花费和长度数值一样的铜板的。比如长度为20的 金条，不管切成长度多大的两半，都要花费20个铜板。一群人想整分整块金 条，怎么分最省铜板？

例如,给定数组{10,20,30}，代表一共三个人，整块金条长度为 10+20+30=60. 金条要分成10,20,30三个部分。 如果， 先把长度60的金条分成10和50，花费60 再把长度50的金条分成20和30，花费50 一共花费110铜板。

但是如果， 先把长度60的金条分成30和30，花费60 再把长度30金条分成10和20，花费30 一共花费90铜板。输入一个数组，返回分割的最小代价。

标准的哈夫曼编码问题

子节点合并在一起的代价，是加起来的和。

最终要把所有的叶节点，生成一棵树。

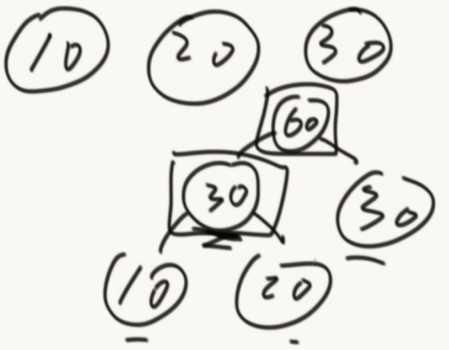
把数组变为小根堆，然后从堆里面取出两个组成树，在把组成的父结点，放入堆中...（如此反复）最后代价就是产生的所有非叶节点。（贪心算法，每次从小根堆里面拿最小的）

 

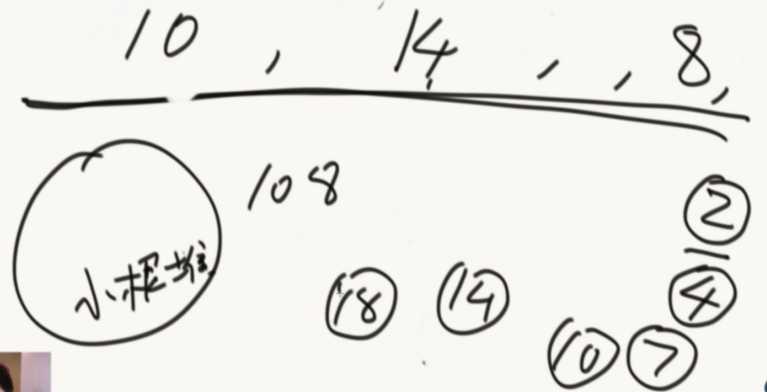
顺序是从上面往下面切割。

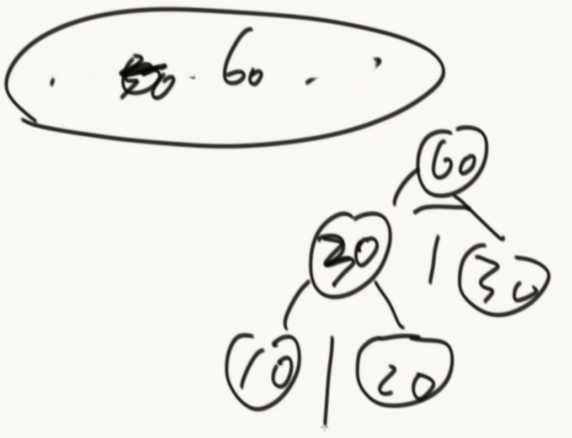
当这种代价，是有子代价累加/乘，一种累什么的，也可能给一个公式，这都有可能用哈夫曼编码贪出来。

要具备起概念思想，用到其他的题目中。

public class Code_02_Less_Money {

    public static int lessMoney(int[] arr) {
        //优先队列是小根堆
        PriorityQueue<Integer> pQ = new PriorityQueue<>();
        for (int i = 0; i < arr.length; i++) {
            pQ.add(arr[i]);
        }
        int sum = 0;
        int cur = 0;
        while (pQ.size() > 1) {
            cur = pQ.poll() + pQ.poll();
            sum += cur;
            pQ.add(cur);
        }
        return sum;
    }

    public static class MinheapComparator implements Comparator<Integer> {
        //输入参数的顺序都为 5  3
        //如果返回 正数（证明后面的比较小） 第二个参数排在前面   5 - 3 = 2  3排在前面
        //如果返回 负数（证明后面的比较大） 第一个参数排在前面   3 - 5 = -2 5排在前面
        //0代表两个东西一样大
        //总结：负一、正二（解决的是哪个参数排在前面）
        @Override
        public int compare(Integer o1, Integer o2) {
            return o1 - o2; // < 0  o1 < o2  负数
        }

    }

    public static class MaxheapComparator implements Comparator<Integer> {

        //等于是-(o1-o2) = o2 - o1
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1; // <   o2 < o1
        }

    }

    public static void main(String[] args) {
        // solution
        int[] arr = { 6, 7, 8, 9 };
        System.out.println(lessMoney(arr));

        int[] arrForHeap = { 3, 5, 2, 7, 0, 1, 6, 4 };

        // min heap
        PriorityQueue<Integer> minQ1 = new PriorityQueue<>();
        for (int i = 0; i < arrForHeap.length; i++) {
            minQ1.add(arrForHeap[i]);
        }
        while (!minQ1.isEmpty()) {
            System.out.print(minQ1.poll() + " ");
        }
        System.out.println();

        // min heap use Comparator
        PriorityQueue<Integer> minQ2 = new PriorityQueue<>(new MinheapComparator());
        for (int i = 0; i < arrForHeap.length; i++) {
            minQ2.add(arrForHeap[i]);
        }
        while (!minQ2.isEmpty()) {
            System.out.print(minQ2.poll() + " ");
        }
        System.out.println();

        // max heap use Comparator
        PriorityQueue<Integer> maxQ = new PriorityQueue<>(new MaxheapComparator());
        for (int i = 0; i < arrForHeap.length; i++) {
            maxQ.add(arrForHeap[i]);
        }
        while (!maxQ.isEmpty()) {
            System.out.print(maxQ.poll() + " ");
        }

    }

}

 

项目收益最大化问题：

输入： 参数1，正数数组costs 参数2，正数数组profits 参数3，正数k 参数4，正数m

costs[i]表示i号项目的花费 profits[i]表示i号项目在扣除花费之后还能挣到的钱(利润) k表示你不能并行、只能串行的最多做k个项目 m表示你初始的资金

说明：你每做完一个项目，马上获得的收益，可以支持你去做下一个 项目。

输出： 你最后获得的最大钱数。

两个数组cost和profit，通过下标列出每个项目的花费和利润，做完项目后所得是cost+forfit，假设有资金W，一次只能做一个项目，最多做K个项目。输出获得最大的钱数。

 

贪心策略。

 

 

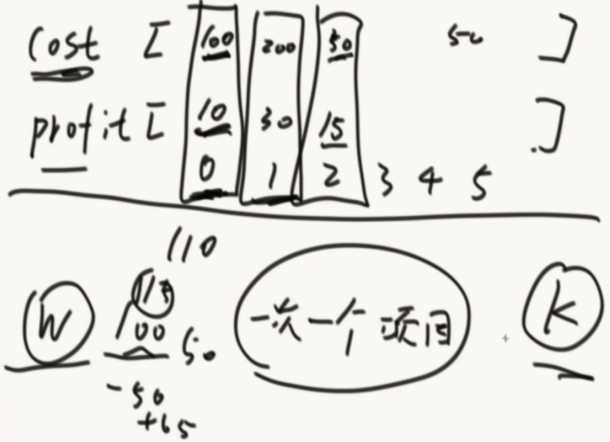
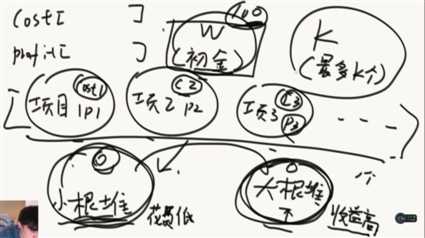
首先项目类型包括花费和利润，再根据花费放入小根堆中，然后看初始资金，在小根堆里面依次弹出头部，只要花费比W低的全部弹出。然后根据收益放入大根堆中，然后做大根堆的第一个项目。

 

当初始资金增加了，再看看小根堆中哪些项目可以做的，继续扔到大根堆中。一直做K个结束（或者大根堆里面没项目可做）。

public class Code_03_IPO {
    public static class Node {
        public int p;
        public int c;

        public Node(int p, int c) {
            this.p = p;
            this.c = c;
        }
    }

    public static class MinCostComparator implements Comparator<Node> {

        @Override
        public int compare(Node o1, Node o2) {
            return o1.c - o2.c;
        }

    }

    public static class MaxProfitComparator implements Comparator<Node> {

        @Override
        public int compare(Node o1, Node o2) {
            return o2.p - o1.p;
        }

    }

    public static int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) {
        Node[] nodes = new Node[Profits.length];
        for (int i = 0; i < Profits.length; i++) {
            nodes[i] = new Node(Profits[i], Capital[i]);
        }

        PriorityQueue<Node> minCostQ = new PriorityQueue<>(new MinCostComparator());
        PriorityQueue<Node> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());
        for (int i = 0; i < nodes.length; i++) {
            minCostQ.add(nodes[i]);
        }
        for (int i = 0; i < k; i++) {
            //先把能做的项目存在大根堆中
            while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) {
                maxProfitQ.add(minCostQ.poll());
            }
            if (maxProfitQ.isEmpty()) {
                return W;
            }
            W += maxProfitQ.poll().p;
        }
        return W;
    }

}

 

随时取中位数

一个数据流中，随时可以取得中位数（之前讲过，初级2 020143）

 

不用堆的话，就用一个容器，吐出一个数就装一个，因为无序的所以装的时候也是无序的。当想要中位数的时候，要排个序，牺牲大。

 

 

准备两个堆，一个大根堆一个小根堆。

第一个数进入大根堆，下一个数小于等于就进大根堆。

如果从大根堆弹出一个数，就拿最后的一个数和第一个数交换，然后heapsize界限-1。

 

 

看题目怎么做：

先把数加入到大根堆中，如果发现两个堆大小差值超过了1，就把较大的弹出一个放到另外一个去。

如果要查中位数，大根堆堆顶和小根堆堆顶肯定能计算出来，因为

大根堆收集了较小的2分之N个，堆顶是其中的最大值。

小根堆收集的是较大的2分之N个，堆顶是其中的最小值。

正好卡在中间的位置。

只要当前数不是小于等于大根堆的，就扔到小根堆中。

策略是固定的：

1、如果当前数小于等于大根堆的堆顶，到大根堆，否则小根堆

2、不平衡了拿出扔到少的堆里面。

这样随时可以拿到中位数。

堆很好用（调整只和层数相关、o(logn)），几乎搞定所有贪心的题目。（面试也经常考）

优先级队列就是堆。

 

 

 

public class Code_04_MadianQuick {

    public static class MedianHolder {
        private PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(new MaxHeapComparator());
        private PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>(new MinHeapComparator());

        private void modifyTwoHeapsSize() {
            if (this.maxHeap.size() == this.minHeap.size() + 2) {
                this.minHeap.add(this.maxHeap.poll());
            }
            if (this.minHeap.size() == this.maxHeap.size() + 2) {
                this.maxHeap.add(this.minHeap.poll());
            }
        }

        public void addNumber(int num) {
            if (this.maxHeap.isEmpty()) {
                this.maxHeap.add(num);
                return;
            }
            if (this.maxHeap.peek() >= num) {
                this.maxHeap.add(num);
            } else {
                if (this.minHeap.isEmpty()) {
                    this.minHeap.add(num);
                    return;
                }        
                if (this.minHeap.peek() > num) {
                    this.maxHeap.add(num);
                } else {
                    this.minHeap.add(num);
                }
            }
            modifyTwoHeapsSize();
        }

        public Integer getMedian() {
            int maxHeapSize = this.maxHeap.size();
            int minHeapSize = this.minHeap.size();
            if (maxHeapSize + minHeapSize == 0) {
                return null;
            }
            Integer maxHeapHead = this.maxHeap.peek();
            Integer minHeapHead = this.minHeap.peek();
            //n & 1 判断奇偶数
            //n&1是n和1做“按位与”运算
            //1的二进制只有末位是1,所以n&1就是只保留n的末位（二进制）.n&1就表示了n的奇偶性.
            if (((maxHeapSize + minHeapSize) & 1) == 0) {//两个堆的数量相同
                //如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。
                return (maxHeapHead + minHeapHead) / 2;
            }
            //如果大/小根堆数量多中间数就在大/小根堆的堆顶。
            return maxHeapSize > minHeapSize ? maxHeapHead : minHeapHead;
        }

    }

    public static class MaxHeapComparator implements Comparator<Integer> {
        @Override
        public int compare(Integer o1, Integer o2) {
            if (o2 > o1) {
                return 1;
            } else {
                return -1;
            }
        }
    }

    public static class MinHeapComparator implements Comparator<Integer> {
        @Override
        public int compare(Integer o1, Integer o2) {
            if (o2 < o1) {
                return 1;
            } else {
                return -1;
            }
        }
    }

    // for test
    public static int[] getRandomArray(int maxLen, int maxValue) {
        int[] res = new int[(int) (Math.random() * maxLen) + 1];
        for (int i = 0; i != res.length; i++) {
            res[i] = (int) (Math.random() * maxValue);
        }
        return res;
    }

    // for test, this method is ineffective but absolutely right
    public static int getMedianOfArray(int[] arr) {
        int[] newArr = Arrays.copyOf(arr, arr.length);
        Arrays.sort(newArr);
        int mid = (newArr.length - 1) / 2;
        if ((newArr.length & 1) == 0) {
            return (newArr[mid] + newArr[mid + 1]) / 2;
        } else {
            return newArr[mid];
        }
    }

    public static void printArray(int[] arr) {
        for (int i = 0; i != arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        boolean err = false;
        int testTimes = 200000;
        for (int i = 0; i != testTimes; i++) {
            int len = 30;
            int maxValue = 1000;
            int[] arr = getRandomArray(len, maxValue);
            MedianHolder medianHold = new MedianHolder();
            for (int j = 0; j != arr.length; j++) {
                medianHold.addNumber(arr[j]);
            }
            if (medianHold.getMedian() != getMedianOfArray(arr)) {
                err = true;
                printArray(arr);
                break;
            }
        }
        System.out.println(err ? "Oops..what a fuck!" : "today is a beautiful day^_^");

    }

}

 

 

宣讲会安排

一些项目要占用一个会议室宣讲，会议室不能同时容纳两个项目的宣讲。给你每一个项目开始的时间和结束的时间(给你一个数组，里面是一个个具体的项目)，你来安排宣讲的日程，要求会议室进行的宣讲的场次最多。返回这个最多的宣讲场次。

 

安排最早开始的先进行，是不行的，如果那项目持续一天，其他项目都讲不来了了。

 

按照持续时间短来安排，也得不到最优解。如果一个小项目卡在两个大项目中间，阻碍了大项目的安排，也不是最优解。

 

根据哪个项目早结束安排。

 

public class Code_06_BestArrange {

    public static class Program {
        public int start;
        public int end;

        public Program(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }

    public static class ProgramComparator implements Comparator<Program> {

        @Override
        public int compare(Program o1, Program o2) {
            return o1.end - o2.end;
        }

    }

    public static int bestArrange(Program[] programs, int start) {
        Arrays.sort(programs, new ProgramComparator());
        int result = 0;
        for (int i = 0; i < programs.length; i++) {
            if (start <= programs[i].start) {
                result++;
                start = programs[i].end;
            }
        }
        return result;
    }

    public static void main(String[] args) {

    }

}

 

贪心策略就是经验式的东西（依靠累计）。不用纠结于证明。