POJ 3784 Running Median

Posted 2021-02-06 lipeiyi520

Description

For this problem, you will write a program that reads in a sequence of 32-bit signed integers. After each odd-indexed value is read, output the median (middle value) of the elements received so far.

Input

The first line of input contains a single integer P, (1 ≤ P ≤ 1000), which is the number of data sets that follow. The first line of each data set contains the data set number, followed by a space, followed by an odd decimal integer M, (1 ≤ M ≤ 9999), giving the total number of signed integers to be processed. The remaining line(s) in the dataset consists of the values, 10 per line, separated by a single space. The last line in the dataset may contain less than 10 values.

Output

For each data set the first line of output contains the data set number, a single space and the number of medians output (which should be one-half the number of input values plus one). The output medians will be on the following lines, 10 per line separated by a single space. The last line may have less than 10 elements, but at least 1 element. There should be no blank lines in the output.

Sample Input

3 
1 9 
1 2 3 4 5 6 7 8 9 
2 9 
9 8 7 6 5 4 3 2 1 
3 23 
23 41 13 22 -3 24 -31 -11 -8 -7 
3 5 103 211 -311 -45 -67 -73 -81 -99 
-33 24 56

Sample Output

1 5
1 2 3 4 5
2 5
9 8 7 6 5
3 12
23 23 22 22 13 3 5 5 3 -3 
-7 -3
题目大意：
输??个序列。

请分别求出前1、3、5、7、9……个数字的中位数

解题思路：

 

维护一个大根堆和一个小根堆，让他们的??保持?多差1。
如果??差距?于1，取出较?的堆的?个堆顶放到另?堆?即可。
询问中位数时，较?的堆的堆顶就是答案。
感谢PoPoQQQ简明易懂的配图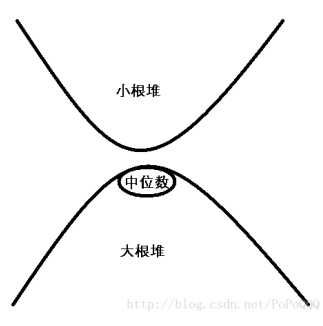

 

AC代码：

 1 #include<iostream>
 2 #include<cstring>
 3 #include<queue>
 4 using namespace std;
 5 int p,m,k,pp,mid,ans[100000];
 6 priority_queue<int> a;//大根堆 
 7 priority_queue<int ,vector<int>, greater<int> > b;//小根堆 
 8 int main() {
 9     cin >> p;
10     for(int i = 1; i <= p; i++) {
11         cin >> pp >> m;
12         int xb = 0;
13         memset(ans, 0,sizeof(ans));
14         while(!a.empty()) a.pop();//初始化 
15         while(!b.empty()) b.pop();//初始化 
16         for(int x = 1;x <= m; ++x) {
17             cin >> k;
18             if(x==1) b.push(k);
19             else{
20                 if(k > b.top()) b.push(k);//如果比中位数大，就扔到小根堆里 
21                 else if(k < b.top()) a.push(k);//如果比中位数小 ，就扔到大根堆里  
22                 if(k == b.top()) {//如果等于中位数，就放到元素较少的堆里 
23                     if(a.size() > b.size()) b.push(k);
24                     else a.push(k);
25                 }
26             }
27             
28             if(a.size() >= b.size() + 2) {//保持两个堆元素数量相差小于二 
29                 b.push(a.top());
30                 a.pop();
31                 mid = a.top();
32             }
33             else if(a.size() + 2 <= b.size()) {//保持两个堆元素数量相差小于二 
34                 a.push(b.top());
35                 b.pop();
36                 mid = b.top();
37             }
38             if(a.size() > b.size()) mid = a.top();
39             if(b.size() > a.size()) mid = b.top();//中位数为元素较多的堆的堆顶 
40             if(x % 2 == 1) {
41                 xb++;
42                 ans[xb] = mid;
43             }
44         
45          }
46         cout << pp << ‘ ‘  << xb <<endl;
47         for(int x = 1;x <= xb;++x){
48             if(x > 10 && x % 10 == 1) cout << endl;
49             cout << ans[x] << " ";
50         }
51         cout << endl;
52     }
53     
54     
55     return 0;
56 }