6-1 为什么要研究树结构 6-2 二分搜索树基础

Posted 2021-02-06 make-big-money

6-1 为什么要研究树结构

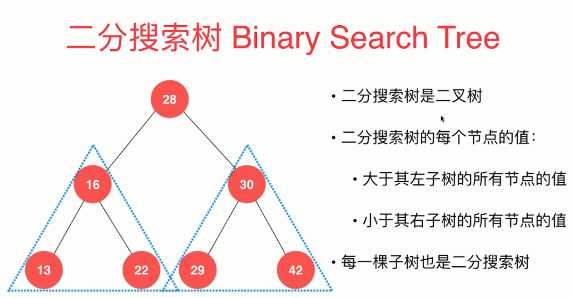
  6-2 二分搜索树基础

 

 

 

 

---恢复内容结束---

6-1 为什么要研究树结构

  6-2 二分搜索树基础

 

 

 

 

---恢复内容开始---

6-1 为什么要研究树结构

  6-2 二分搜索树基础

 

 

 

 

---恢复内容结束---

6-1 为什么要研究树结构

  6-2 二分搜索树基础

 

 

 

 

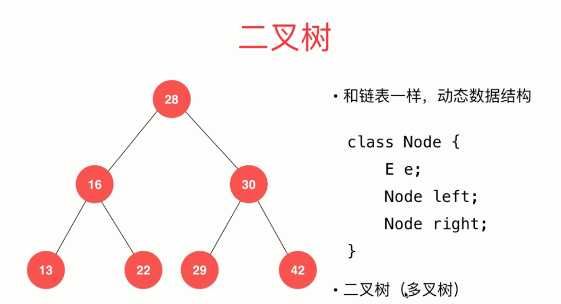
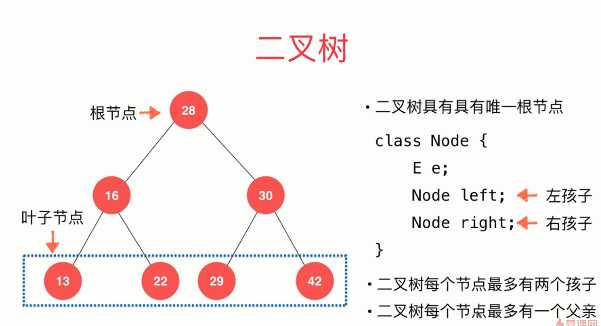
二分搜索树基本代码

 1 public class BST<E extends Comparable<E>> {//对于二分搜索树所存储的内容支持泛型，所以在这里写一个E，此外二分搜索树不是支持所有的类型，对这个类型必须要有限制,
 2                                                  //这个限制是这个类型必须拥有可比较性，放到代码中，就必须对E进行限制，即E extends Comparable<E>（E要满足可比较性）
 3     private class Node {  //声明节点类
 4         public E e;//节点可以存放元素e
 5         public Node left, right;//成员变量
 6 
 7         public Node(E e) {  //node的构造函数，用户传来一个e
 8             this.e = e;//this.e等于用户传来的e（用户传来的参数和节点类成员变量元素均用e表示，所以节点存放元素用this.e表示）
 9             left = null;
10             right = null;
11         }
12     }
13     //二分搜索树的成员变量root、size
14     private Node root; //root:根节点
15     private int size;//size:记录二分搜索树存储了多少元素
16 
17     public BST(){  //二分搜索树的构造函数
18         root = null;  //初始化时二分搜索树一个元素也没有存，根节点root为空
19         size = 0;
20     }
21 
22     public int size(){
23         return size;
24     }
25 
26     public boolean isEmpty(){
27         return size == 0;
28     }
29 }