产品排序(2015 年北大自招夏令营) （与栈相关的区间DP）

Posted 2021-02-06 812-xiao-wen

题面:

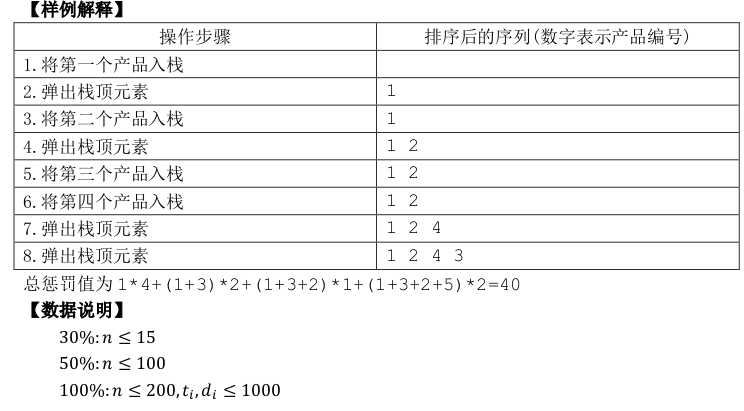
(solution:)

又是一道(DP)的好题啊！状态并不明显，需要仔细分析，而且还结合了栈的特性！

做这一类题，只要出题人有点理想，一定会在栈的性质上做点文章，所以我们尽量围绕栈的性质设置(DP)状态。可是栈又有什么性质呢？讲真，考场我是真没想到，好像压根就不知道有这个特性：

对于队列里([l,r])范围内的数，必然存在一个最晚出栈的(iin[l,r])，而我们不难发现此时([l,i-1])必然比([i+1,r])出栈要早一些，因为([i+1,r])进栈之前(i)就已经进栈了，而(i)又是最后一个出栈的（也就是说在(i)进栈时栈里一定是空的！！！不然：假设还有一个(j)未弹出，(i)进栈时会在(j上面)，那么最晚出栈的就将会是(j)！！！）

所以不论([l,i-1])的顺序是怎样的，他们对于后面的数所产生的（时间之和）与（惩罚值之和）是确定的！！！而此时如果我们知道([l,i-1],[i+1,r])的总（时间之和）与（惩罚值之和）就能知道([l,r])的总（时间之和）与（惩罚值之和）。所以我们应该先用这个方法先求([l,i-1])与([i+1,r])的最小（时间之和）与（惩罚值之和）再来得出([l,r])。

转移方程：

(f[l][r]=min(f[l][r],f[l][i-1]+f[i+1][r]+(st[i-1]-st[l-1])*(sd[r]-sd[i])+(st[r]-st[l-1])*d[i]))

其中：

1. (i)是需要在([l,r])内枚举的
2. (f[l][i-1])与(f[i+1][r])是先前就求好了的
3. ((st[i-1]-st[l-1])*(sd[r]-sd[i])) :这个是因为([i+1,r])在([l,i-1])后面，所以等待的时间增加了(（[l,i-1])的时间总和，从而总惩罚值也要相应增加。
4. ((st[r]-st[l-1])*d[i])) ：(i)是最后一个出栈的，它的惩罚值要乘上整个区间的时间和

唉！现在一想明明如此浅显的道理我怎么在考场上就是想不到呢？？？果然还是太弱了，唉.........

(code:)

#include<iostream>
#include<cstdio>
#include<iomanip>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<ctime>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
#include<set>

#define ll long long
#define db double
#define inf (ll)40000000001
#define rg register int

using namespace std;

int n;
int t[205];
int d[205];
ll st[205];
ll sd[205];
ll f[205][205];

inline int qr(){
    char ch;
    while((ch=getchar())<'0'||ch>'9');
    int res=ch^48;
    while((ch=getchar())>='0'&&ch<='9')
        res=res*10+(ch^48);
    return res;
}

int main(){
    //freopen("product.in","r",stdin);
    //freopen("product.out","w",stdout);
    n=qr();
    for(rg i=1;i<=n;++i){
        t[i]=qr(),d[i]=qr();
        st[i]=st[i-1]+t[i];
        sd[i]=sd[i-1]+d[i];
    }
    for(rg i=1;i<=n;++i)
        for(rg j=i;j<=n;++j)
            f[i][j]=i==j?t[i]*d[i]:inf;
    for(rg k=1;k<=n;++k)
        for(rg l=1;l<=n-k;++l)
            for(rg i=l,r=l+k;i<=r;++i)
                f[l][r]=min(f[l][r],f[l][i-1]+f[i+1][r]+(st[i-1]-st[l-1])*(sd[r]-sd[i])+(st[r]-st[l-1])*d[i]);
    printf("%lld
",f[1][n]);
    return 0;
}