无向图的割顶和桥，无向图的双连通分量入门详解及模板 -----「转载」

Posted 2020-10-30 hyghb

https://blog.csdn.net/stillxjy/article/details/70176689

 

割顶和桥：对于无向图G，如果删除某个节点u后，连通分量数目增加，则称u为图的割顶；如果删除某条边后，连通分量数目增加，则称该边为图的桥。对于连通图删除割顶或桥后都会使得图不再连通

以下我，我们利用dfs的性质来快速找出一个连通图中的所有的割顶和桥
首先我们要引入”时间戳”这个概念：

时间戳：表示在进行dfs时，每个节点被访问的先后顺序。每个节点会被标记两次，分别用pre[],和post[]表示。
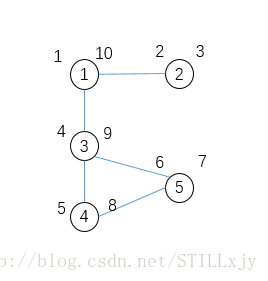
例如下图的时间戳表示：（节点左上角为pre[],右上角为post[],子节点的访问顺序按照编号从小到达访问）

图中的边分类：
树边与反向边：在进行dfs时某条边u-v,若v还没有被访问，则u-v为树边，若v已经被访问过则u-v为反向边。
对于上图的DFS树，下图中实线为树边，虚线为反向边

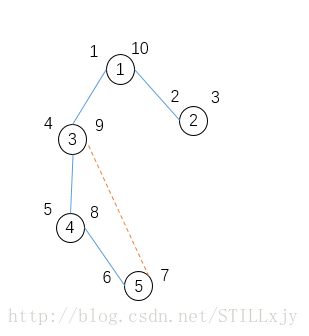
在无向图中除了树边就是反向边，且不存在跨越两棵子树的边
所以对于根节点而言，如果有两个及以上节点则根节点为割顶，否则不是
对于其他节点：在无向连通图G的DFS树中，非根节点u是割顶当且仅当u存在一个子节点v，使得v及其所有后代都没有反向边连回u的祖先（不包括u）
以上判断条件很好想，只要随便画画草图就可以了

了解以上知识后我们找出图中所有的割顶和桥
设low[u]为u及其后代所能连回的最早的祖先的pre[]值，则当u存在一个子节点v使得low[v] >= pre[u]时u就为割顶
同理当 low[v] > pre[u]时 u-v为桥

求图中割顶和桥的代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>
using namespace std;

const int maxn = 1000;

int n,m;
vector<int> G[maxn];
int low[maxn],pre[maxn];
int dfs_clock;     //时间戳
int iscut[maxn];   //标记是否为割顶

int dfs(int u,int fa)
{
    int lowu = pre[u] = ++dfs_clock;
    int child = 0;
    for(int i=0;i<G[u].size();i++)
    {
        int v = G[u][i];
        if(!pre[v])     //没有访问的v
        {
            child++;    //孩子节点的数目
            int lowv = dfs(v,u);
            lowu = min(lowu,lowv);    //用后代更新lowu
            if(lowv >= pre[u]) iscut[u] = 1;
            if(lowv > pre[u]) cout<<"桥："<<u<<"-"<<v<<endl;
        }
        else if(pre[v] < pre[u] && v != fa)  //用反向边更新lowu
        {
            lowu = min(lowu,pre[v]);
        }
    }
    if(fa < 0 && child == 1) iscut[u] = 0;    //对于根节点的处理
    low[u] = lowu;
    return lowu;
}


int main()
{
    freopen("in.txt","r",stdin);
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        memset(pre,0,sizeof(pre));
        memset(iscut,0,sizeof(iscut));
        for(int i=0;i<=n;i++) G[i].clear();
        int u,v;
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&u,&v);
            G[u].push_back(v);
            G[v].push_back(u);
        }

        dfs(1,-1);
        for(int i=1;i<=n;i++) if(iscut[i])
            cout<<i<<endl;
    }
    return 0;
}

点_双连通分量 BCC：
对于一个连通图，如果任意两点至少存在两条“点不重复”的路径，则说图是点双连通的（即任意两条边都在一个简单环中），点双连通的极大子图称为点_双连通分量。
易知每条边属于一个连通分量，且连通分量之间最多有一个公共点，且一定是割顶

点_双连通分量代码模板：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>
#include <stack>
using namespace std;

const int maxn = 1000;

struct Edge   //栈中边的结构
{
    int u,v;
    Edge(int uu,int vv)
    {
        u = uu;
        v = vv;
    }
};
stack<Edge> s;

struct edge  //链式前向星建图的边结构
{
    int v,next;
}edges[maxn];

int n,m;        //节点的数目，无向边的数目
int e,head[maxn];
int pre[maxn];           //第一次访问的时间戳
int dfs_clock;           //时间戳
int iscut[maxn];         //标记节点是否为割顶
int bcc_cnt;             //点_双连通分量的数目
int bccno[maxn];         //节点属于的点_双连通分量的编号
vector<int> bcc[maxn];   //点_双连通分量

void addedges(int u,int v)  //加边
{
    edges[e].v = v;
    edges[e].next = head[u];
    head[u] = e++;
    edges[e].v = u;
    edges[e].next = head[v];
    head[v] = e++;
}

int dfs(int u,int fa)
{
    int lowu = pre[u] = ++dfs_clock;
    int child = 0;
    for(int i=head[u];i!=-1;i=edges[i].next)
    {
        int v = edges[i].v;
        Edge e = (Edge){u,v};
        if(!pre[v])
        {
            s.push(e);
            child++;
            int lowv = dfs(v,u);
            lowu = min(lowu,lowv); //用后代更新lowu
            if(lowv >= pre[u])     //找到了一个子树满足割顶的条件
            {
                iscut[u] = 1;
                bcc_cnt++;
                bcc[bcc_cnt].clear();
                for(;;)            //保存bcc信息
                {
                    Edge x = s.top(); s.pop();
                    if(bccno[x.u] != bcc_cnt) {bcc[bcc_cnt].push_back(x.u); bccno[x.u] = bcc_cnt;}
                    if(bccno[x.v] != bcc_cnt) {bcc[bcc_cnt].push_back(x.v); bccno[x.v] = bcc_cnt;}
                    if(x.u == u && x.v == v) break;
                }
            }
        }
        else if(pre[v] < pre[u] && v != fa)   //用反向边更新lowu
        {
            s.push(e);
            lowu = min(lowu,pre[v]);
        }
    }
    if(fa < 0 && child == 1) iscut[u] = 0;    //对于根节点若只有一个子树则不是割顶
    return lowu;
}

void init()
{
    memset(pre,0,sizeof(pre));
    memset(iscut,0,sizeof(iscut));
    memset(head,-1,sizeof(head));
    memset(bccno,0,sizeof(bccno));
    e = 0; dfs_clock = 0; bcc_cnt = 0;
}

int main()
{
    int u,v;
    freopen("in.txt","r",stdin);
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init();
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&u,&v);
            addedges(u,v);
        }
        dfs(1,-1);
        for(int i=1;i<=bcc_cnt;i++)
        {
            for(int j=0;j<bcc[i].size();j++)
                cout<<bcc[i][j]<<" ";
            cout<<endl;
        }

    }
    return 0;
}

代码讲解：在理解了上面找割顶的代码后，以上求BCC的代码就是用一个栈保存所有的访问的边，然后在找到一个割顶之后就将该割顶信息全部出栈后保存起来即可。（具体实现细节要自己手写代码验证最好，详见代码）

边_双连通分量 EBC：
对于边_双连通分量的求解简单多了，我们先找出所有的桥，并将其做上标记。然后在利用dfs遍历连通分量即可，只需在遍历时不能访问桥即可。

边_双连通分量代码模板

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>
using namespace std;

const int maxn = 1000;
struct Edge
{
    int no,v,next;      //no：边的编号
}edges[maxn];

int n,m,ebcnum;         //节点数目，无向边的数目，边_双连通分量的数目
int e,head[maxn];
int pre[maxn];          //第一次访问的时间戳
int dfs_clock;          //时间戳
int isbridge[maxn];     //标记边是否为桥
vector<int> ebc[maxn];  //边_双连通分量

void addedges(int num,int u,int v)    //加边
{
    edges[e].no = num;
    edges[e].v = v;
    edges[e].next = head[u];
    head[u] = e++;
    edges[e].no = num++;
    edges[e].v = u;
    edges[e].next = head[v];
    head[v] = e++;
}

int dfs_findbridge(int u,int fa)    //找出所有的桥
{
    int lowu = pre[u] = ++dfs_clock;
    for(int i=head[u];i!=-1;i=edges[i].next)
    {
        int v = edges[i].v;
        if(!pre[v])
        {
            int lowv = dfs_findbridge(v,u);
            lowu = min(lowu,lowv);
            if(lowv > pre[u])
            {
                isbridge[edges[i].no] = 1; //桥
            }
        }
        else if(pre[v] < pre[u] && v != fa)
        {
            lowu = min(lowu,pre[v]);
        }
    }
    return lowu;
}

void dfs_coutbridge(int u,int fa)     //保存边_双连通分量的信息
{
    ebc[ebcnum].push_back(u);
    pre[u] = ++dfs_clock;
    for(int i=head[u];i!=-1;i=edges[i].next)
    {
        int v = edges[i].v;
        if(!isbridge[edges[i].no] && !pre[v]) dfs_coutbridge(v,u);
    }
}

void init()
{
    memset(pre,0,sizeof(pre));
    memset(isbridge,0,sizeof(isbridge));
    memset(head,-1,sizeof(head));
    e = 0; ebcnum = 0;
}

int main()
{
    int u,v;
    freopen("in.txt","r",stdin);
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        init();
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&u,&v);
            addedges(i,u,v);
        }
        dfs_findbridge(1,-1);
        memset(pre,0,sizeof(pre));
        for(int i=1;i<=n;i++)
        {
            if(!pre[i])
            {
                ebc[ebcnum].clear();
                dfs_coutbridge(i,-1);
                ebcnum++;
            }
        }
        for(int i=0;i<ebcnum;i++)
        {
            for(int j=0;j<ebc[i].size();j++)
                cout<<ebc[i][j]<<" ";
            cout<<endl;
        }
    }
    return 0;
}

以上都是本人看了白书（《算法竞赛入门经典——训练指南》）后对相关知识点的总结，若有不清楚的地方可以直接去看课本，或者留下评论，谢谢