JZOJ 5230. 队伍统计

Posted 2021-02-06 zjzjzj

题目

Description

现在有n个人要排成一列，编号为1->n 。但由于一些不明原因的关系，人与人之间可能存在一些矛盾关系，具体有m条矛盾关系(u,v),表示编号为u的人想要排在编号为v的人前面。要使得队伍和谐，最多不能违背k条矛盾关系（即不能有超过k条矛盾关系(u,v),满足最后v排在了u前面）。问有多少合法的排列。答案对10^9+7取模。

 

Input

输入文件名为count.in。
第一行包括三个整数n,m,k。
接下来m行，每行两个整数u,v,描述一个矛盾关系(u,v)。
保证不存在两对矛盾关系(u,v),(x,y)，使得u=x且v=y 。

Output

输出文件名为count.out。
输出包括一行表示合法的排列数。

 

Sample Input

输入1：
4 2 1
1 3
4 2

输入2：
10 12 3
2 6
6 10
1 7
4 1
6 1
2 4
7 6
1 4
10 4
10 9
5 9
8 10

Sample Output

输出1：
18

输出2：
123120

 

Data Constraint

对于30%的数据，n<=10
对于60%的数据，n<=15
对应100%的数据，n,k<=20,m<=n*(n-1)，保证矛盾关系不重复。

 

分析

 

•  一道状压DP（不会啊啊啊啊）

• 考试时，稳稳地打了暴力 30
• 后来才理解
• 状压，顾名思义就是要将一些状压想办法压缩起来（可以压，也可以删）。其中这些状态都满足相似性和数量很多。这样才好压而且压得有意义。
• 所以一般基础的状压就是将一行的状态压成一个数，这个题用数的二进制形式反映了一种情况。所以位运算可以帮助我们解决很多问题。
• 这道题，我们将冲突的数用二进制放在a数组里
• 然后我们用二进制数来代表n位的选取情况
• 进行DP  f[i][j] 表示在二进制表示的第i种选取情况下有j种矛盾的情况数
• 转移方程就是f[当前已改变的集合][j+冲突个数]+=没改变前的种数f[i][j]
• 然后对于每个i 我们还要枚举对第x位进行一次选取，计算出答案
• （位运算分析具体在代码里）

 

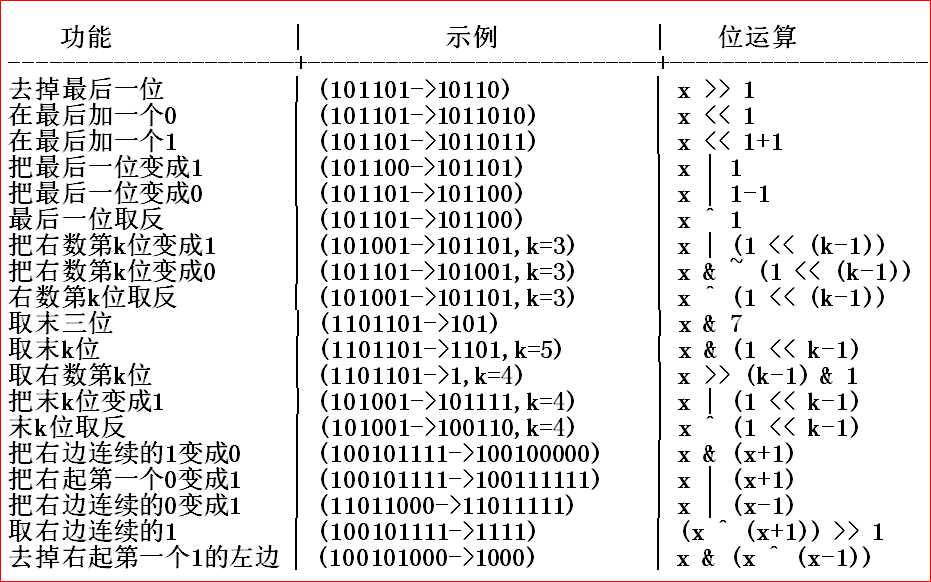
代码

 1 #include<fstream>
 2 #define M 1000000007
 3 #define cin fin
 4 #define cout fout
 5 using namespace std;
 6 ifstream fin("count.in");
 7 ofstream fout ("count.out");
 8 int a[21],f[1<<21][21],t[1<<21];
 9 int n,m,k;
10 void take()    //计算所有集合中1的个数 也就是选取的个数 
11 {
12     for (int i=0;i<=(1<<n)-1;i++)
13     {
14         int ii=i;
15         while (ii)
16         {
17             t[i]++;
18             ii-=(ii&(-ii));     //(ii&(-ii))找到最后的1位置，然后减去 
19         }
20     }
21 }
22 int main ()
23 {
24     ios::sync_with_stdio(false);   //cin优化 
25     cin>>n>>m>>k;
26     for (int i=1,u,v;i<=m;i++)
27     {
28         cin>>u>>v;
29         a[u]|=(1<<(v-1));   //用二进制，来反应它的冲突 例： 
30     }                        // 首先数组为    00000 
31     take();                  // 现在与3冲突了 00100  第三位 1 
32     f[0][0]=1;               // 又与 4 冲突了 01100  第四位变1 
33    for(int i=0;i<=(1<<n)-1;i++)  //所以这就表示出来了，当前数u与其他数的冲突情况 
34      for(int j=0;j<=k;j++)
35       if(f[i][j])
36         for(int x=1;x<=n;x++)
37           if((i&(1<<(x-1)))==0)   // 表示当前集合与要变的位置没有变过 
38 /*因为t记录的是（上面）t[i&a[x]]为冲突个数*/if(j+t[i&a[x]]<=k)    //例 1010 x=2 1010 & 0100 无改变
39                 f[i|(1<<(x-1))][j+t[i&a[x]]]=(f[i|(1<<(x-1))][j+t[i&a[x]]]+f[i][j])%M;
40     int ans=0;
41     for (int i=0;i<=k;i++)
42        ans=(ans+f[(1<<n)-1][i])%M;
43     cout<<ans;
44 }