RMQ问题 常用解法
Posted -wallace-
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了RMQ问题 常用解法相关的知识,希望对你有一定的参考价值。
( ext{0-RMQ})概况
(RMQ(Range Minimum/Maximum Query))问题是指:对于长度为(n)的数列(A),回答若干询问(RMQ(A,i,j)(i,j<=n)),返回数列(A)中下标在(i),(j)里的最小(大)值,也就是说,(RMQ)问题是指求区间最值的问题。
本文所采用的例题Luogu P3865。
题目所述“请注意最大数据时限只有0.8s,数据强度不低,请务必保证你的每次查询复杂度为O(1)”,而这里却不止一种解法。
( ext{I-}O(n^2))解法
朴素做法:
对于每个询问,从(A_i)扫到(A_j),途中记录最大值即可,这里就不贴Code了。
( ext{II-}O(n imessqrt n))解法
分块(平方分割)
将原序列(A)分割成许多“块”,并由(pos_i)标记(A_i)位于的块序号,由(Max_i)来管理第(i)块的最大值。对于每个询问:
- 若(pos_i=pos_j),直接暴力;
- 若(pos_i e pos_j),会出现“整块”和“边角块”,边角块暴力即可,整块直接取(Max)中的值。
代码:
//[Template]Sqrt Block
//Luogu P3865 【模板】ST表
//https://www.luogu.org/problemnew/show/P3865
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e6+10;
const int M=1e6+10;
const int SQRTN=1e3*2;
const int size=1000;
int n,m;
int A[N];
int Max[SQRTN];
int pos[N];
inline int Query_max(int l,int r)
{
register int i;int res=-0x3f3f3f3f;
if(pos[r]==pos[l])
{
for(i=l;i<=r;i++)
res=max(res,A[i]);
return res;
}
for(i=l;i<=pos[l]*size;i++)
res=max(res,A[i]);
for(i=pos[l]+1;i<=pos[r]-1;i++)
res=max(res,Max[i]);
for(i=(pos[r]-1)*size+1;i<=r;i++)
res=max(res,A[i]);
return res;
}
int main()
{
register int i;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
scanf("%d",&A[i]),pos[i]=(i/size)+1;
for(i=1;i<=n;i++)
Max[pos[i]]=max(Max[pos[i]],A[i]);
while(m--)
{
int l,r;
scanf("%d%d",&l,&r);
printf("%d
",Query_max(l,r));
}
return 0;
}效率略逊于BIT等数据结构,可能会TLE,但比起朴素做法,也有较大优势。而且分块好理解,而且拓展性较高。
( ext{III-}O(n imes log(n)))解法
( ext{III-1-} Segment Tree) 线段树
总的来说,比LG的P3372简单多了(不用(lazy-tag)了)。
每个节点维护最大值,但其实只要数组即可。
代码:
//[Template]Segment Tree
//Luogu P3865 【模板】ST表
//https://www.luogu.org/problemnew/show/P3865
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e6+10;
const int M=1e6+10;
const int ROOT=1;
int Max[4*N];
int A[N];
int n,m;
void Build(int rt,int l,int r)
{
if(l==r)
{
Max[rt]=A[l];
return;
}
Build(rt<<1,l,(l+r)>>1);
Build(rt<<1|1,((l+r)>>1)+1,r);
Max[rt]=max(Max[rt<<1],Max[rt<<1|1]);
return;
}
int Query_max(int rt,int l,int r,int x,int y)
{
if(x<=l&&y>=r)return Max[rt];
if(x>r||y<l)return -0x3f3f3f3f;
return max(Query_max(rt<<1,l,(l+r)>>1,x,y),Query_max(rt<<1|1,((l+r)>>1)+1,r,x,y));
}
int main()
{
register int i;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
scanf("%d",&A[i]);
Build(ROOT,1,n);
while(m--)
{
int l,r;
scanf("%d%d",&l,&r);
printf("%d
",Query_max(ROOT,1,n,l,r));
}
return 0;
}理解以后,线段树查询的用途几乎是最广的。
( ext{III-3-} Binary Index Tree) 树状数组
BIT的空间、代码长度都比线段树更优。但是比较难理解的。比如:
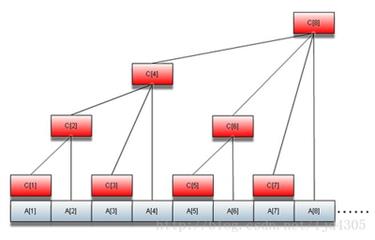
显然,它的空间省了许多而且更快。
//[Template]Binary Index Tree
//Luogu P3865 【模板】ST表
//https://www.luogu.org/problemnew/show/P3865
#include<cstdio>
#include<iostream>
#define lowbit(x) (x&-x)
using namespace std;
const int N=1e6;
const int M=1e6;
int Max[N];
int n,cnt,temp,m;
int a[N];
inline void Add(int x)
{
int low, i;
while (x<=n)
{
Max[x]=a[x];
low=lowbit(x);
for (i=1;i<low;i<<=1)
Max[x]=max(Max[x],Max[x-i]);
x+=lowbit(x);
}
}
int Query_max(int x, int y)
{
int ans=0;
while (y>=x)
{
ans=max(a[y], ans);
y--;
while(y-lowbit(y)>=x)
{
ans=max(Max[y],ans);
y-=lowbit(y);
}
}
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++)
scanf("%d",&a[i]),Add(i);
for(register int i=1,x,y;i<=m;i++)
{
scanf("%d%d",&x,&y);
printf("%d
",Query_max(x,y));
}
return 0;
}线段树虽然在许多方面逊于BIT,但之所以有线段树的存在,是因为线段树能适用于很多方面,不仅仅是区间、单点的查询修改,还有标记等等,可以用于模拟、DP等等。
参考:https://tjor.blog.luogu.org/xian-duan-shu-yu-shu-zhuang-shuo-zu
( ext{III-4} ST)表
ST表是一种初始化(O(nlogn)),而查询只要(O(1))的高效算法。
我们用(Max[i][j])表示,从(i)位置开始的(2^j)个数中的最大值,例如(Max[i][1])表示的是(i)位置和(i+1)位置中两个数的最大值
那么转移的时候我们可以把当前区间拆成两个区间并分别取最大值(注意这里的编号是从(1)开始的)
查询的时候也比较简单
我们计算出(log_2{ ext{区间长度}})
然后对于左端点和右端点分别进行查询,这样可以保证一定可以覆盖查询的区间:
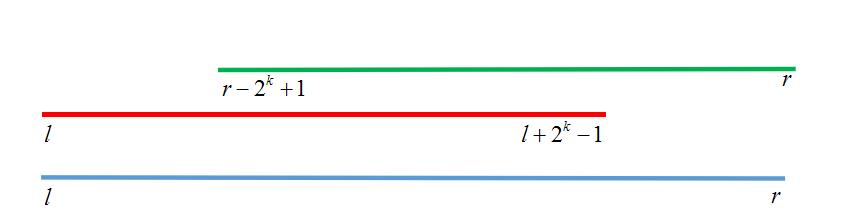
代码:
//[Template]ST Table
//Luogu P3865 【模板】ST表
//https://www.luogu.org/problemnew/show/P3865
#include<cstdio>
#include<cmath>
#include<iostream>
using namespace std;
const int N=1e6+10;
const int M=1e6+10;
int n,m;
int Max[N][21];//从i位置开始的2^j个数中的最大值
//a * (2^n) 等价于 a<< n
inline int Query_max(int l,int r)
{
int k=log2(r-l+1);
return max(Max[l][k],Max[r-(1<<k)+1][k]);
}
int main()
{
register int i,j;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)
scanf("%d",&Max[i][0]);
for(j=1;j<=21;j++)
for(int i=1;i+(1<<j)-1<=n/*===>>[i+2^j-1<=N]*/;i++)
Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))/*i+2^(j-1)*/][j-1]);
for(i=1;i<=m;i++)
{
int l,r;
scanf("%d%d",&l,&r);
printf("%d
",Query_max(l,r));
}
return 0;
}目前,最优的算法。
参考:http://www.cnblogs.com/zwfymqz/p/8581995.html
( ext{IV-})EXT拓展:
(RMQ)问题还可以有笛卡尔树或莫队的做法,这里就不再写了。(其实我不会)
暂时在此。
以上是关于RMQ问题 常用解法的主要内容,如果未能解决你的问题,请参考以下文章