基础数论

Posted 2021-02-05 ljc20020730

/*
今天的基础数论我觉得我还是重新温习一下比较好！
*/

时光是个迷，当时初二的我在XX学堂挺这种东西恐怕和各位高一党一个水平吧。

我还是写写吧，希望对大家有点用！

知识点1：快速幂（卡粟米）

求a^p其实可以用分治的思想来求

 

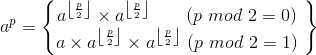
就是不断的分治，直到p=0，返回1.

递归写法：

const int mo=100000007;
int pow(int x,int n)
{
    if (n==0) return 1;
    if (n==1) return x;
    int t=pow(x,n/2)%mo;
    t=t*t%mo;
    if (n%2) t=t*x%mo;
    return t;
}

非递归写法：

int pow(int x,int n,int p)
{
    int ans=1;
    while (n) {
        if (n&1) ans=ans*x%p;
        x=x*x%p;
        n>>=1;
    }
    return ans%p;
}

知识点2：质数

定理1：唯一分解定理（任何大于2正整数都可以表示成为多个质数相乘的形式，并且分解唯一）

定理2：素数判断定理（当且仅当不存在任意1<k<=（下取整） √x，使得x mod k = 0，那么x为质数）

定理3：整数1，既不是质数又不是合数！

质数的判定：（试除法O（√x）、非完美算法米勒罗宾随机算法）

埃拉托斯特尼筛法求质数O(n log log n)

• 若x是质数那么从x²开始，把x的倍数筛去。

 

void EratosthenesSha(int n)
{
    memset(prime,true,sizeof(prime));
    vector<int>a;a.clear();
    for (int i=2;i<=n;i++) {
        if (prime[i]==false) continue;
        a.push_back(i);
        for (int j=i+i;j<=n;j+=i) prime[j]=false;
    }
}

 

欧拉线性筛法求质数O(n)

• 每个合数都只筛一次（用最小质因子筛去），给当前的数i乘上一个质因子，有更小的质因子或者超出范围break
• 为什么？由于i若是prime[j]的倍数，i*prime[j+1]（等）一定被筛过：由于i=k*prime[j]，i*prime[j+1]=k*prime[j]*prime[j+1]这个数i*prime[j]最小质因子一定不是prime[j+1]不用删去，这样就保证每个数删去一次！

 

void EouLaSha(int lim)
{
    int cnt=0;
    pr[0]=pr[1]=true;
    for (int i=2;i<=lim;i++) {
        if (!pr[i]) prime[cnt++]=i;
        for (int j=0;j<cnt&&i*prime[j]<=lim;j++) {
            pr[i*prime[j]]=true;
            if (i%prime[j]==0) break;
        }
    }
}

知识点3：gcd和exgcd（扩展欧几里得）

• gcd（欧几里得算法）

求出gcd(a,b)就是求出a和b的最大公因数。

定理： gcd(a,b)=gcd(b,a%b)

证明：∀r，满足r|a，r|b; 而

　　　

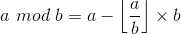
　　　r|a mod b 且 r|b

　　　由定义可知，r|a,r|b且r任意，可以为a，b的最大公因数。

　　    证毕。

 

int gcd(int a,int b)
{
    if (b==0) return a;
    return simple_gcd(b,a%b);
   // 代码更短： return (!b)?a:simple_gcd(b,a%b); 
}

 

• exgcd（扩展欧几里得算法）

对于下列不定方程，必有一对整数解，我们可以通过exgcd求出|x|+|y|最小的一对！

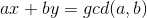
易得4个方程：

 

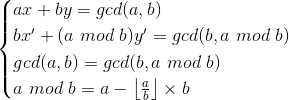
联立解之得（用x‘表示x，y’表示y，a和b是常数）：

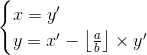
　　　　 特别的，当b=0的时候，方程组变成了ax=gcd(a,0)=a，得a=1，人为定义y=0

　　　　

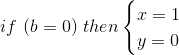
int ex_gcd(int a,int b,int &x,int &y)
{
    if (b==0) {
        x=1;y=0;
        return a;
    }
    int r=ex_gcd(b,a%b,x,y);
    int t=x;x=y;y=t-a/b*y;
    return r;
}

知识点4：同余方程和同余方程

同余的定义：若a mod p = b mod p ，那么称a与b关于p同余，记作a≡b (mod p)

同余的定理：

 

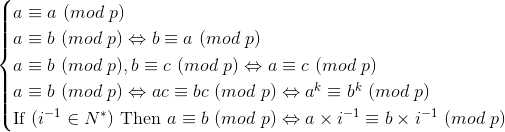
乘法逆元的定义:若ax≡1（mod p），那么称x为a在模p意义下的逆(元),记做 a^-1

求逆元的方法：

快速幂求逆元：

费马小定理：若p为素数，a为正整数，且a和p互质，有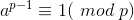  

推出：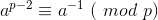

/*
基于费马小定理pow(a,p-2)%p 就是a在mod p意义下的逆元
*/
int pow(int x,int n,int m)
{
    if (n==0) return 1;
    if (n==1) return x;
    int t=pow(x,n/2,m)%m;
    t=t*t%m;
    if (n%2) t=t*x%m;
    return t;
}
int inv(int x,int m)
{
    return pow(x,m-2,m)%m;
}

扩展欧几里得求逆元

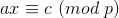 c=1是1等价于：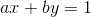

求出x的正根即可

/*
求ax=1(mod p)
就是求ax%p=1,所以ax ax=kp+1,就是ax-kp=1，
当p为质数的时候gcd(a,-p)=1，求此时x的值就是逆元
注意模到正数就行
*/
int ex_gcd(int a,int b,int &x,int &y)
{
    if (b==0) {
        x=1;y=0;
        return a;
    }
    int r=ex_gcd(b,a%b,x,y);
    int t=x;x=y;y=t-a/b*y;
    return r;
}
int inv(int a,int m)
{
    int x,y;
    int g=ex_gcd(a,m,x,y);
    return (x+m)%m;
}

筛选法求逆元

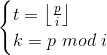
有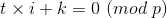  

两边乘上 i^-1k^-1

得：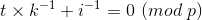

那么，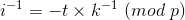

即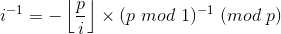

void getinv(int x,int p)
{
    memset(inv,0,sizeof(inv)); 
    inv[1]=1;
    for (int i=2;i<=x;i++)
     inv[i]=(long long)(p-p/i)%p*inv[p%i]%p;
}