方差 线段树

Posted 2021-02-05 zxyqzy

题目背景

滚粗了的HansBug在收拾旧数学书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本数学书里面发现了一个神奇的数列，包含N个实数。他想算算这个数列的平均数和方差。

输入输出格式

输入格式：

第一行包含两个正整数N、M，分别表示数列中实数的个数和操作的个数。

第二行包含N个实数，其中第i个实数表示数列的第i项。

接下来M行，每行为一条操作，格式为以下两种之一：

操作1：1 x y k ，表示将第x到第y项每项加上k，k为一实数。

操作2：2 x y ，表示求出第x到第y项这一子数列的平均数。

操作3：3 x y ，表示求出第x到第y项这一子数列的方差。

输出格式：

输出包含若干行，每行为一个实数，即依次为每一次操作2或操作3所得的结果（所有结果四舍五入保留4位小数）。

输入输出样例

输入样例#1： 复制

5 5
1 5 4 2 3
2 1 4
3 1 5
1 1 1 1
1 2 2 -1
3 1 5

输出样例#1： 复制

3.0000
2.0000
0.8000

说明

样例说明：

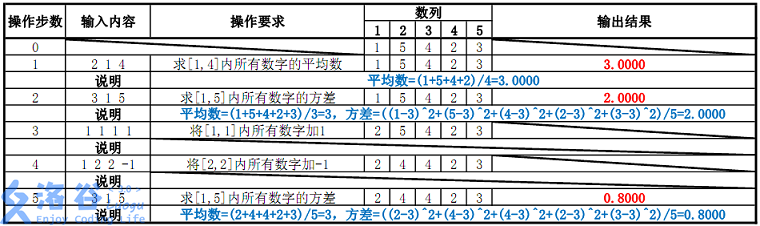
数据规模：

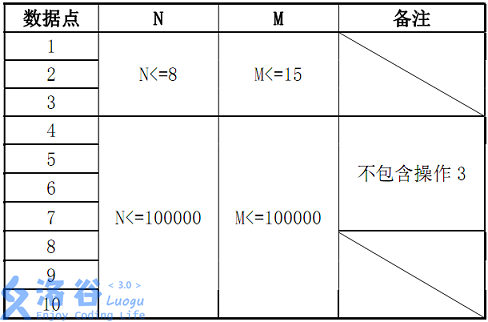
注意 pushdown ；

一定要先更新 x^2的下传，因为 x^2 要根据 x ；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize(2)
using namespace std;
#define maxn 200005
#define inf 0x7fffffff
//#define INF 1e18
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-4
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == ‘-‘) f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
int sqr(int x) { return x * x; }


/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/
struct node {
	double sum1;
	double sum2;
	double add;
}t[maxn<<2];
double a[maxn];
int n, m;
void pushup(int rt) {
	t[rt].sum1 = t[rt << 1].sum1 + t[rt << 1 | 1].sum1;
	t[rt].sum2 = t[rt << 1].sum2 + t[rt << 1 | 1].sum2;
}

void pushdown(int rt,int len) {
	if (t[rt].add) {
		t[rt << 1].add += t[rt].add;
		t[rt << 1 | 1].add += t[rt].add;
		t[rt << 1].sum2 += 2 * t[rt].add*t[rt<<1].sum1 + (len - len / 2)*t[rt].add*t[rt].add;
		t[rt << 1 | 1].sum2 += 2 * t[rt].add*t[rt << 1 | 1].sum1 + (len / 2)*t[rt].add*t[rt].add;
		t[rt << 1].sum1 += t[rt].add*(len - len / 2);
		t[rt << 1 | 1].sum1 += t[rt].add*(len / 2);
		t[rt].add = 0;
	}
}

void build(int l, int r, int rt) {
	t[rt].add = 0;
	if (l == r) {
		t[rt].sum1 = a[l];
		t[rt].sum2 = a[l] * a[l]; return;
	}
	int mid = (l + r) >> 1;
	build(l, mid, rt << 1); build(mid + 1, r, rt << 1 | 1);
	pushup(rt);
}

void upd(int L, int R, int l, int  r, int rt, double val) {
	if (L <= l && r <= R) {
		t[rt].add += val;
		t[rt].sum2 += 2 * val*t[rt].sum1 + (r - l + 1)*val*val;
		t[rt].sum1 += (r - l + 1)*val;
		return;
	}
	pushdown(rt, r - l + 1);
	int mid = (r + l) >> 1;
	if (L <= mid)upd(L, R, l, mid, rt << 1, val);
	if (mid < R)upd(L, R, mid + 1, r, rt << 1 | 1, val);
	pushup(rt);
}

double query1(int L, int R, int l, int r, int rt) {
	if (L <= l && r <= R) {
		return 1.0*t[rt].sum1;
	}
	pushdown(rt, r - l + 1);
	double ans = 0.0;
	int mid = (l + r) >> 1;
	if (L <= mid)ans += 1.0*query1(L, R, l, mid, rt << 1);
	if (mid < R)ans += 1.0*query1(L, R, mid + 1, r, rt << 1 | 1);
	return ans * 1.0;
}
double query2(int L, int R, int l, int r, int rt) {
	if (L <= l && r <= R) {
		return 1.0*t[rt].sum2;
	}
	pushdown(rt, r - l + 1);
	int mid = (r + l) >> 1;
	double ans = 0.0;
	if (L <= mid)ans += query2(L, R, l, mid, rt << 1);
	if (mid < R)ans += query2(L, R, mid + 1, r, rt << 1 | 1);
	return 1.0*ans;
}

int main() {
//	ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin >> n >> m;
	for (int i = 1; i <= n; i++)rdlf(a[i]);
	build(1, n, 1);
	while (m--) {
		int op; rdint(op);
		if (op == 1) {
			int x, y;double  k; rdint(x); rdint(y); rdlf(k);
			upd(x, y, 1, n, 1, k);
		}
		else if (op == 2) {
			int x, y;
			rdint(x); rdint(y);
			printf("%.4lf
", 1.0*query1(x, y, 1, n, 1)/(y-x+1)*1.0);
		}
		else if (op == 3) {
			int x, y; rdint(x); rdint(y);
			double M = 1.0*query1(x, y, 1, n, 1) / (y - x + 1);
			double ans = 1.0*query2(x, y, 1, n, 1) / (y - x + 1) - 1.0*M*M;
			printf("%.4lf
", 1.0*ans);
		}
	}
	return 0;
}