麻省理工公开课:线性代数 第2课 矩阵消元
Posted hg-love-dfc
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了麻省理工公开课:线性代数 第2课 矩阵消元相关的知识,希望对你有一定的参考价值。
参考资料:
网易公开课:http://open.163.com/special/opencourse/daishu.html 麻省理工公开课:线性代数
假设求解:
$x+2y+z=2$
$3x+8y+z=12$
$4y+z=2$
一、消元
1. 矩阵形式$Amathbf{x}=b$:
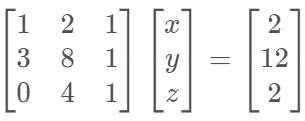
2. 消元过程如下:

矩阵[A b]为增广矩阵,得到的主元(pivot)分别为$1, 2, 5$,矩阵$A$的行列式为主元的乘积;
3. 回代求解
消元后的等式为$Umathbf{x}=c$
$x+2y+z=2$
$2y-2z=6$
$2z=-10$
求解得:$z=-2, y=1, x=2$
4. 行变换的矩阵表示(第1、3行不变,第2行减去第1行的3倍):初等矩阵$E_{21}、E_{32}$
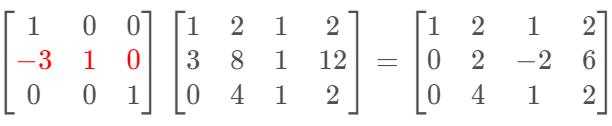
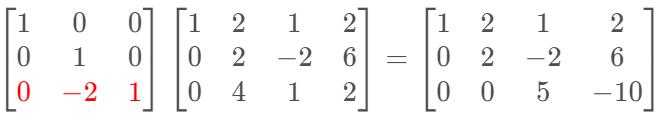
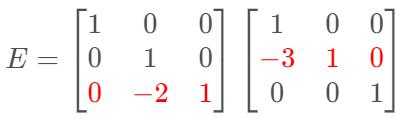
所以,可以得到:$$E_{32}E_{21}Amathbf{x}=EAmathbf{x}=Umathbf{x}$$
注:
- 矩阵左乘列向量$Amathbf{x}$:结果为列向量,应理解为矩阵各列向量的线性组合
- 矩阵右乘行向量$mathbf{y}A$:结果为行向量,应理解为矩阵各行向量的线性组合
5. 置换矩阵P(左乘$PA$交换行,右乘$AP$交换列)
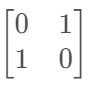
以上是关于麻省理工公开课:线性代数 第2课 矩阵消元的主要内容,如果未能解决你的问题,请参考以下文章