算法分析基础——差消法求解高阶递推方程

Posted 2021-02-05 jeffrey-y

差消法，简单来讲，就是对高阶的递推方程作差，转化为一阶方程后再运用迭代法。有了迭代法的基础后，差消法理解起来就很容易了。这里举出对快速排序的分析加以说明。

对于快排，我们知道选择不同的轴值，会导致不同的算法效率。最坏的情况下，选取的轴值恰好是待排序数组的最值，那么排序的效率就会退化为线性时间。现在我们来估算平均情况下快速排序的时间复杂度。

设T(n)为待排序数组长度为n时，快速排序算法需要的比较次数。那么T(1) = 0，而T(n)的递推方程相对于轴值的选取有如下n种情况：

T(n) = T(0) + T(n - 1) + n - 1

T(n) = T(1) + T(n - 2) + n - 1

...

T(n) = T (n - 1) + T(0) + n - 1

假定选取的轴值在排序后的数组中的每个位置出现的概率相等。那么平均情况下，就可以计算得到T(n)的递推表达式为

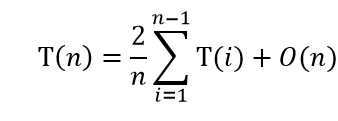
这是n阶的递推方程，不适合直接采用迭代法。接下来即运用差消法来求解：将O(n)用cn来表达，得到

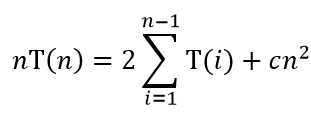
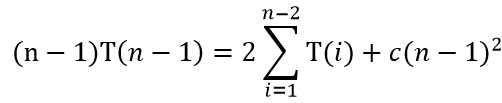
两式相减得

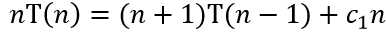
再同除以n(n+1)，得到熟悉的一阶递推方程

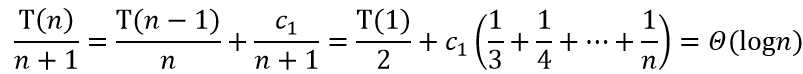
于是我们得出T(n) = Θ(nlogn)。