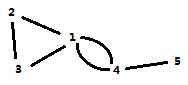Tarjan算法
Posted antigonae
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Tarjan算法相关的知识,希望对你有一定的参考价值。
写在前面:
Tarjan全家桶
Tarjan的代码除了Tarjan求LCA外,长得都一样,分清楚细微差别就好了
关于代码,我是复制了第一个板子后删改写出来的,长得极为相似,很多地方只有两三行不一样,建议双屏逐行对比一下看看具体哪里不一样
需要特别注意的是,在无向图中,边双连通分量需要用边标记法,而点双连通分量需要用点标记法,切勿弄混
非原创内容标明出处

|
目录 |
有向图
|
强连通: 在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通。可知至少要有三个点 强连通图: 如果有向图G的每两个点都强连通,称G是一个强连通图 强连通分量: 有向图G的极大强连通子图,称为强连通分量 ——bia度百科 例子:
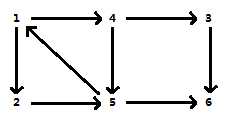
网上用烂的图 1,4强连通 图G‘(包含点1,4,5,2和仅在这四点之间相互连接的5条边)是强连通图 而图G(包含所有点,所有边)不是强连通图 上述图G‘是图G的一个(这里也是唯一一个)极大强连通子图(它不能再拓展,再拓展就不是强连通图),即强连通分量 |
思路:
搜索 → 优化的搜索(保证每个点必然且仅仅搜索1次,且记录每个点搜索的顺序) → 引入栈来辅助
具体来说,是从某个点开始,带着两个信息minTime(思路上,栈中的元素是按照minTime分组的)和vTime(每个点唯一一次被搜索时的次序)去拓展
如果某个点在某个组(即某个强连通分量)里,那么它的minTime(原来等于它本身的vTime)必然会被更新(更新成该强连通分量里点的最小的minTime,有可能是它自己)
在每一次搜索后,都去比对刚刚搜过的点的minTime和vTime一不一样,如果一样,那么就把它和它后面的所有点(如果有的话)全部清出栈,而每一次清出来的一组点(它们的minTime相同)就是一个强连通分量
代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=100010,MAXM=100010; 6 int n,m; 7 8 //------Tarjan------ 9 int vTime[MAXN],minTime[MAXN],Vtime; 10 //------Tarjan------ 11 12 //------手写栈------ 13 int index,stackk[MAXM]; 14 bool vis[MAXN]; 15 //------手写栈------ 16 17 //------存图------ 18 int heads[MAXN],numedge=1,u,v; 19 struct EDGE{ 20 int next,to; 21 }edge[MAXM]; 22 inline void adde(int u,int v){ 23 ++numedge; 24 edge[numedge].next=heads[u]; 25 edge[numedge].to=v; 26 heads[u]=numedge; 27 } 28 //------存图------ 29 30 void tarjan(int x) 31 { 32 vTime[x]=minTime[x]=++Vtime; 33 stackk[++index]=x;vis[x]=1;//维护栈来找强连通分量 34 for(int i=heads[x];i!=0;i=edge[i].next) 35 { 36 if(!vTime[edge[i].to])//能拓展的点仍未访问过 37 { 38 tarjan(edge[i].to); 39 minTime[x]=min(minTime[x],minTime[edge[i].to]); 40 } 41 else if(vis[edge[i].to])//能拓展的点访问过,且在栈里面 42 { 43 minTime[x]=min(minTime[x],vTime[edge[i].to]); 44 } 45 } 46 47 /*每搜索一个点后*/ 48 if(minTime[x]==vTime[x]){ 49 //printf("【 ");for(int i=1;i<=index;i++)printf("%d ",stackk[i]);printf("】 "); 50 //上面这行用来查看栈里有什么 51 do{ 52 printf("%d ",stackk[index]); 53 vis[stackk[index]]=0; 54 index--; 55 }while(stackk[index+1]!=x); 56 printf(" "); 57 } 58 return; 59 } 60 61 int main(int argc,char* argv[], char* enc[]) 62 { 63 scanf("%d%d",&n,&m); 64 for(int i=1;i<=m;++i){ 65 scanf("%d%d",&u,&v); 66 adde(u,v); 67 } 68 69 for(int i=1;i<=n;++i) 70 if(!vTime[i]) tarjan(i);//如果没有被搜索过,就搜索这个点 71 72 return 0; 73 }
测试数据:
|
6 8 1 4 |
无向图
|
边双连通: 无向图G中,对于一个连通图,如果任意两点至少存在两条“边不重复”的路径(点可以重复),则说图是边双连通的 边双连通分量: 边双连通的极大子图称为边双连通分量 |
思路:
Tarjan求强通分量 → 转化为无向图(记录从哪条边搜过来的防止在两点之间重复搜索)
具体来说,就是套用有向图求强连通分量的思路,加上在无向边中防止在两点间来回搜索的技巧(用边标记,别用父子节点标记,否则无法判断两点之间多条边的情况)
我们使用的是边标记法,而不是父子节点标记法,判断两点之间的多条边就很轻松了
代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=100010,MAXM=100010; 6 int n,m; 7 8 //------Tarjan------ 9 int vTime[MAXN],minTime[MAXN],Vtime; 10 //------Tarjan------ 11 12 //------手写栈------ 13 int index,stackk[MAXM]; 14 bool vis[MAXN]; 15 //------手写栈------ 16 17 //------存图------ 18 int heads[MAXN],numedge=1,u,v; 19 struct EDGE{ 20 int next,to; 21 }edge[MAXM<<1]; 22 inline void adde(int u,int v){ 23 ++numedge;//格外注意这里,第一条边的编号是2 24 edge[numedge].next=heads[u]; 25 edge[numedge].to=v; 26 heads[u]=numedge; 27 } 28 //------存图------ 29 30 void tarjan(int x,int sEdge)//sEdge表示搜到这点的边 31 { 32 vTime[x]=minTime[x]=++Vtime; 33 stackk[++index]=x;vis[x]=1;//维护栈来找边双连通分量 34 for(int i=heads[x];i!=0;i=edge[i].next) 35 { 36 if(!vTime[edge[i].to])//即下一个点仍未访问过 37 { 38 tarjan(edge[i].to,i); 39 minTime[x]=min(minTime[x],minTime[edge[i].to]);//更新,同下 40 } 41 else if(i!=(sEdge^1))//下一个点访问过,且不是同一条边,即出现双联通分量,另外注意位运算符的优先级比较低,需要括号 42 { 43 minTime[x]=min(minTime[x],vTime[edge[i].to]);//更新,同上 44 } 45 } 46 47 /*每搜索一个点后*/ 48 if(minTime[x]==vTime[x]){ 49 //printf("【 ");for(int i=1;i<=index;i++)printf("%d ",stackk[i]);printf("】 "); 50 //上面这行用来查看栈里有什么 51 do{ 52 printf("%d ",stackk[index]); 53 vis[stackk[index]]=0; 54 index--; 55 }while(stackk[index+1]!=x); 56 printf(" "); 57 } 58 return; 59 } 60 61 int main(int argc,char* argv[], char* enc[]) 62 { 63 scanf("%d%d",&n,&m); 64 for(int i=1;i<=m;++i){ 65 scanf("%d%d",&u,&v); 66 adde(u,v),adde(v,u); 67 } 68 69 for(int i=1;i<=n;++i) 70 if(!vTime[i]) tarjan(i,0); 71 72 return 0; 73 }
测试数据:
|
5 5
5 6 2 3 2 1 3 1 4 1 4 1 4 5 |
无向图
|
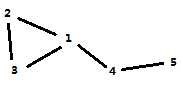
桥(割边): 边双连通分量G去掉某一条边后就不是边双连通分量,那么这条边就是桥(割边) 或者说,边双连通分量G‘去掉某一条边后边连通块的个数增加,那么这条边就是桥(割边) ——http://www.cnblogs.com/zwfymqz/p/8480552.html 例子:
图G‘(包含点2,1,3和三点之间的3条无向边)是边双连通的,且是边双连通分量 去掉边1-4或边4-5后,图G‘就不是边双连通分量,则这两条边都是桥(割边) |
思路:
Tarjan求边双连通分量 → 比较搜索的相邻两点之间的minTime和vTime判断是不是桥
具体来说,就是套用求边双连通分量的思路,加上判定桥(割边)的技巧
每次搜索一个点Ti的回溯过程中,如果它连接的点Ti+1的minTime>Ti本身的vTime,那么说明它之后的点没有其他路径回到这个点,这两个点之间的这一条边是他们连通的唯一路径,就是桥(割边)
特殊地,如果两条点之间有两条及以上的边(重边),或者两条以上的路径,那么这两条边都不是桥(割边)
而我们使用的是边标记法(防止在两点之间重复搜索的标记法),而不是父子节点标记法,判断两点之间的多条边就很轻松了
代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=100010,MAXM=100010; 6 int n,m; 7 8 //------Tarjan------ 9 int vTime[MAXN],minTime[MAXN],Vtime; 10 //------Tarjan------ 11 12 //------存图------ 13 int heads[MAXN],numedge=1,u,v; 14 struct EDGE{ 15 int next,to; 16 }edge[MAXM<<1]; 17 inline void adde(int u,int v){ 18 ++numedge;//格外注意这里,第一条边的编号是2 19 edge[numedge].next=heads[u]; 20 edge[numedge].to=v; 21 heads[u]=numedge; 22 } 23 //------存图------ 24 25 void tarjan(int x,int sEdge)//sEdge表示搜到这点的边 26 { 27 vTime[x]=minTime[x]=++Vtime; 28 for(int i=heads[x];i!=0;i=edge[i].next) 29 { 30 if(!vTime[edge[i].to])//即下一个点仍未访问过 31 { 32 tarjan(edge[i].to,i); 33 34 minTime[x]=min(minTime[x],minTime[edge[i].to]);//更新,同下 35 if(minTime[edge[i].to]>vTime[x]) 36 printf("桥%d-%d ",edge[i].to,x); 37 //minTime[edge[i].to]>vTime[x],即后面的点无法回到x点之前 38 } 39 else if(i!=(sEdge^1))//下一个点访问过,且不是同一条边,即出现双联通分量,另外注意位运算符的优先级比较低,需要括号 40 { 41 minTime[x]=min(minTime[x],vTime[edge[i].to]);//更新,同上 42 } 43 } 44 return; 45 } 46 47 int main(int argc,char* argv[], char* enc[]) 48 { 49 scanf("%d%d",&n,&m); 50 for(int i=1;i<=m;++i){ 51 scanf("%d%d",&u,&v); 52 adde(u,v),adde(v,u); 53 } 54 55 for(int i=1;i<=n;++i) 56 if(!vTime[i]) tarjan(i,0); 57 58 return 0; 59 }
测试数据:
5 5
5 6 2 3 2 1 3 1 4 1 4 1 4 5 |
无向图
|
点双连通: 无向图G中,对于一个连通图,如果任意两点至少存在两条“点不重复”的路径(边可以重复),则说图是点双连通的 点双连通分量: 点双连通的极大子图称为点双连通分量 |
思路:
Tarjan求强通分量 → 转化为无向图(记录从哪条边搜过来的防止在两点之间重复搜索)
具体来说,就是套用有向图求强连通分量的思路,加上在无向边中防止在两点间来回搜索的技巧(用父子节点标记,别用边标记)
我们使用的是父子节点标记法,而不是边标记法,这样得到的才是点双连通分量
代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=100010,MAXM=100010; 6 int n,m; 7 8 //------Tarjan------ 9 int vTime[MAXN],minTime[MAXN],Vtime; 10 //------Tarjan------ 11 12 //------手写栈------ 13 int index,stackk[MAXM]; 14 bool vis[MAXN]; 15 //------手写栈------ 16 17 //------存图------ 18 int heads[MAXN],numedge=1,u,v; 19 struct EDGE{ 20 int next,to; 21 }edge[MAXM<<1]; 22 inline void adde(int u,int v){ 23 ++numedge; 24 edge[numedge].next=heads[u]; 25 edge[numedge].to=v; 26 heads[u]=numedge; 27 } 28 //------存图------ 29 30 void tarjan(int x,int fa)//fa表示搜到这点的父节点 31 { 32 vTime[x]=minTime[x]=++Vtime; 33 stackk[++index]=x;vis[x]=1;//维护栈来找点双连通分量 34 for(int i=heads[x];i!=0;i=edge[i].next) 35 { 36 if(!vTime[edge[i].to])//即仍未访问过 37 { 38 tarjan(edge[i].to,x); 39 minTime[x]=min(minTime[x],minTime[edge[i].to]); 40 } 41 else if(edge[i].to!=fa) 42 { 43 minTime[x]=min(minTime[x],vTime[edge[i].to]); 44 } 45 } 46 47 /*每搜索一个点后*/ 48 if(minTime[x]==vTime[x]){ 49 //printf("【 ");for(int i=1;i<=index;i++)printf("%d ",stackk[i]);printf("】 "); 50 //上面这行用来查看栈里有什么 51 do{ 52 printf("%d ",stackk[index]); 53 vis[stackk[index]]=0; 54 index--; 55 }while(stackk[index+1]!=x); 56 printf(" "); 57 } 58 return; 59 } 60 61 int main(int argc,char* argv[], char* enc[]) 62 { 63 scanf("%d%d",&n,&m); 64 for(int i=1;i<=m;++i){ 65 scanf("%d%d",&u,&v); 66 adde(u,v),adde(v,u); 67 } 68 69 for(int i=1;i<=n;++i) 70 if(!vTime[i]) tarjan(i,i); 71 72 return 0; 73 }
测试数据:
|
5 5
5 6 2 3 2 1 3 1 4 1 4 1 4 5 |
无向图
|
割点: 无向图G去掉某一个点后剩余的点就不能每一个相互到达,那么这个点就是割点 例子:
图G‘(包含点2,1,3和三点之间的3条无向边)是点双连通的,且是点双连通分量 去掉点1或4后,整个图G中剩余的点不能每一个相互到达,那么这两个点就是割点 |
思路:
Tarjan求点双连通分量 → 比较搜索的相邻两点之间的minTime和vTime判断是不是割点
具体来说,就是套用求点双连通分量的思路,加上判定割点的技巧
因为每一次搜索的根结点比较特殊,它的fa就是它自己,不能使用和其子节点一样的方法搜索,所以单独拎出来,即:
①当前节点u不是本次搜索开始的根节点的时候:
在u之后遍历的点,向上翻,最多到u,那么u就是割点
如果能翻到u的前面,那么说明有环,去掉u之后,整个图G中剩余的点每一个都还能相互到达
②当前节点u是本次搜索开始的根节点的时候:
计算其子树数量,如果有2棵即以上的子树,u就是割点
如果去掉这个点,这两棵子树就不能互相到达
代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=100010,MAXM=100010; 6 int n,m; 7 8 //------Tarjan------ 9 int vTime[MAXN],minTime[MAXN],Vtime; 10 //------Tarjan------ 11 12 //------割点需要------ 13 bool iscut[MAXN]; 14 //可能会重复输出一个割点,那么就记录一下 15 //------割点需要------ 16 17 //------存图------ 18 int heads[MAXN],numedge=1,u,v; 19 struct EDGE{ 20 int next,to; 21 }edge[MAXM<<1]; 22 inline void adde(int u,int v){ 23 ++numedge; 24 edge[numedge].next=heads[u]; 25 edge[numedge].to=v; 26 heads[u]=numedge; 27 } 28 //------存图------ 29 30 void tarjan(int x,int fa)//fa表示搜到这点的父节点 31 { 32 vTime[x]=minTime[x]=++Vtime; 33 int child=0;//记录根节点的孩子数 34 for(int i=heads[x];i!=0;i=edge[i].next) 35 { 36 if(!vTime[edge[i].to])//即仍未访问过 37 { 38 tarjan(edge[i].to,x); 39 minTime[x]=min(minTime[x],minTime[edge[i].to]); 40 41 if(x==fa) child++; 42 else if(minTime[edge[i].to]>=vTime[x]) iscut[x]=1; 43 //(minTime[edge[i].to]>=vTime[x])即后面的点无法回到x点之前 44 } 45 else if(edge[i].to!=fa) 46 { 47 minTime[x]=min(minTime[x],vTime[edge[i].to]); 48 } 49 } 50 if(x==fa && child>=2) iscut[x]=1; 51 return; 52 } 53 54 int main(int argc,char* argv[], char* enc[]) 55 { 56 scanf("%d%d",&n,&m); 57 for(int i=1;i<=m;++i){ 58 scanf("%d%d",&u,&v); 59 adde(u,v),adde(v,u); 60 } 61 62 for(int i=1;i<=n;++i) 63 if(!vTime[i]) tarjan(i,i); 64 65 for(int i=1;i<=n;i++) 66 if(iscut[i]) printf("[%d] ",i); 67 68 return 0; 69 }
测试数据:
|
5 5
5 6 2 3 2 1 3 1 4 1 4 1 4 5 |
有向图/无向图
缩点/染色,即消除图中的环,建立了一个新图
消除了环之后,不管是什么样的暴力就都很方便了(某些题目甚至直接缩点+大爆搜能过)
有向图:
Tarjan求强连通分量 → 在执行时顺便加上把强连通分量染色
具体来说,在将一组强连通分量清除出栈时保存一下每个点所在的是哪一个色块以及这个色块的大小(当然还可以搞一下色块出度,色块权值什么的)
在运行完Tarjan搜索后,遍历一遍所有边,可以看看每个色块有没有出度,顺便也可以把色块连出去
为了方便起见,在存图时不仅保存每条边的to,也保存每条边的from
代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=100010,MAXM=100010; 6 int n,m; 7 8 //------Tarjan------ 9 int vTime[MAXN],minTime[MAXN],Vtime; 10 //------Tarjan------ 11 12 //------缩点需要------ 13 int colournum,inColour[MAXN],colourSize[MAXN],colourValue[MAXN],colourTo[MAXN]; 14 bool outDegree[MAXN]; 15 //colournum:集合(色块)的编号 16 //inClolur:u是属于哪个集合(色块)中的 17 //colourSize:集合(色块)所含有的元素个数 18 //colourValue:每个集合(色块)的权值 19 //colourTo:每个集合(色块)连接的下一个色块 20 //outDegree:每个集合(色块)的出度(要么是1要么是0) 21 //------缩点需要------ 22 23 //------手写栈------ 24 int index,stackk[MAXM]; 25 bool vis[MAXN]; 26 //------手写栈------ 27 28 //------存图------ 29 int heads[MAXN],numedge=1,u,v; 30 int value[MAXN];//点的权值 31 struct EDGE{ 32 int next,from,to; 33 }edge[MAXM]; 34 inline void adde(int u,int v){ 35 ++numedge; 36 edge[numedge].next=heads[u]; 37 edge[numedge].from=u; 38 edge[numedge].to=v; 39 heads[u]=numedge; 40 } 41 //------存图------ 42 43 void tarjan(int x) 44 { 45 vTime[x]=minTime[x]=++Vtime; 46 stackk[++index]=x;vis[x]=1;//维护栈来找强连通分量 47 for(int i=heads[x];i!=0;i=edge[i].next) 48 { 49 if(!vTime[edge[i].to])//能拓展的点仍未访问过 50 { 51 tarjan(edge[i].to); 52 minTime[x]=min(minTime[x],minTime[edge[i].to]); 53 } 54 else if(vis[edge[i].to])//能拓展的点访问过,且在栈里面 55 { 56 minTime[x]=min(minTime[x],vTime[edge[i].to]); 57 } 58 } 59 60 /*每搜索一个点后*/ 61 if(minTime[x]==vTime[x]){ 62 //printf("【 ");for(int i=1;i<=index;i++)printf("%d ",stackk[i]);printf("】 "); 63 //上面这行用来查看栈里有什么 64 ++colournum; 65 do{ 66 //printf("%d ",stackk[index]); 67 vis[stackk[index]]=0; 68 69 inColour[stackk[index]]=colournum; 70 ++colourSize[colournum]; 71 colourValue[colournum]+=value[stackk[index]]; 72 73 index--; 74 }while(stackk[index+1]!=x); 75 //printf(" "); 76 } 77 return; 78 } 79 80 int main(int argc,char* argv[], char* enc[]) 81 { 82 scanf("%d%d",&n,&m); 83 for(int i=1;i<=n;++i) scanf("%d",&value[i]); 84 for(int i=1;i<=m;++i){ 85 scanf("%d%d",&u,&v); 86 adde(u,v); 87 } 88 89 for(int i=1;i<=n;++i) 90 if(!vTime[i]) tarjan(i); 91 92 for(int i=2;i<=numedge;++i)//枚举每条边,看看是否有两个色块之间相连,因为是有向图,所以必然有一个色块有出度(如果有就必然是1) 93 if(inColour[edge[i].from]!=inColour[edge[i].to]){ 94 colourTo[inColour[edge[i].from]]=inColour[edge[i].to]; 95 outDegree[inColour[edge[i].from]]=1; 96 } 97 98 for(int i=1;i<=colournum;++i){ 99 printf("now_colcur[%d] size[%d] value[%d]",i,colourSize[i],colourValue[i]); 100 if(outDegree[i]) printf(" to colour %d ",colourTo[i]); 101 else printf(" no out_degree "); 102 } 103 104 return 0; 105 }
测试数据:
|
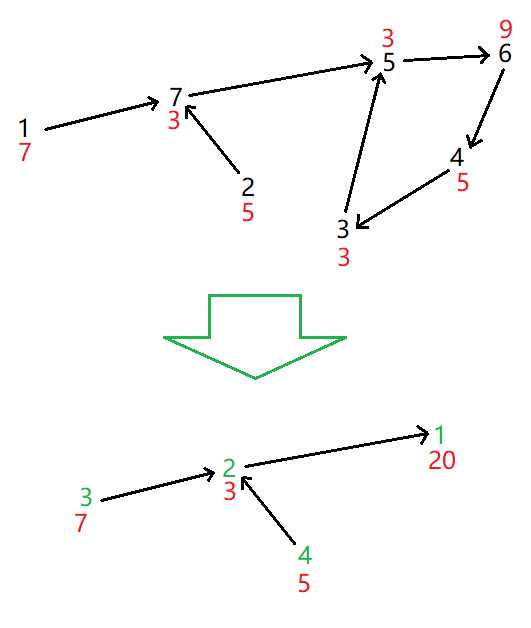
黑色为点编号,红色为权值,绿色为新点的色块号
7 7 |
无向图:
Tarjan求点双连通分量 → 在执行时顺便加上把点双连通分量染色
大体同上,但由于是无向图,建立的新的图上点的连线就有一点麻烦了,这里就不演示连接新点了(有向无环图保证了有出度就是1,很方便存图)
代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=100010,MAXM=100010; 6 int n,m; 7 8 //------Tarjan------ 9 int vTime[MAXN],minTime[MAXN],Vtime; 10 //------Tarjan------ 11 12 //------缩点需要------ 13 int colournum,inColour[MAXN],colourSize[MAXN],colourValue[MAXN]; 14 bool outDegree[MAXN]; 15 //colournum:集合(色块)的编号 16 //inClolur:u是属于哪个集合(色块)中的 17 //colourSize:集合(色块)所含有的元素个数 18 //colourValue:每个集合(色块)的权值 19 //------缩点需要------ 20 21 //------手写栈------ 22 int index,stackk[MAXM]; 23 bool vis[MAXN]; 24 //------手写栈------ 25 26 //------存图------ 27 int heads[MAXN],numedge=1,u,v; 28 int value[MAXN];//点的权值 29 struct EDGE{ 30 int next,from,to; 31 }edge[MAXM]; 32 inline void adde(int u,int v){ 33 ++numedge; 34 edge[numedge].next=heads[u]; 35 edge[numedge].from=u; 36 edge[numedge].to=v; 37 heads[u]=numedge; 38 } 39 //------存图------ 40 41 void tarjan(int x,int fa) 42 { 43 vTime[x]=minTime[x]=++Vtime; 44 stackk[++index]=x;vis[x]=1;//维护栈来找强连通分量 45 for(int i=heads[x];i!=0;i=edge[i].next) 46 { 47 if(!vTime[edge[i].to])//能拓展的点仍未访问过 48 { 49 tarjan(edge[i].to,x); 50 minTime[x]=min(minTime[x],minTime[edge[i].to]); 51 } 52 else if(edge[i].to!=fa) 53 { 54 minTime[x]=min(minTime[x],vTime[edge[i].to]); 55 } 56 } 57 58 /*每搜索一个点后*/ 59 if(minTime[x]==vTime[x]){ 60 //printf("【 ");for(int i=1;i<=index;i++)printf("%d ",stackk[i]);printf("】 "); 61 //上面这行用来查看栈里有什么 62 ++colournum; 63 do{ 64 //printf("%d ",stackk[index]); 65 vis[stackk[index]]=0; 66 67 inColour[stackk[index]]=colournum; 68 ++colourSize[colournum]; 69 colourValue[colournum]+=value[stackk[index]]; 70 71 index--; 72 }while(stackk[index+1]!=x); 73 //printf(" "); 74 } 75 return; 76 } 77 78 int main(int argc,char* argv[], char* enc[]) 79 { 80 scanf("%d%d",&n,&m); 81 for(int i=1;i<=n;++i) scanf("%d",&value[i]); 82 for(int i=1;i<=m;++i){ 83 scanf("%d%d",&u,&v); 84 adde(u,v); 85 adde(v,u); 86 } 87 88 for(int i=1;i<=n;++i) 89 if(!vTime[i]) tarjan(i,i); 90 91 for(int i=1;i<=colournum;++i) 92 printf("now_colcur[%d] size[%d] value[%d] ",i,colourSize[i],colourValue[i]); 93 94 return 0; 95 }
测试数据:
|
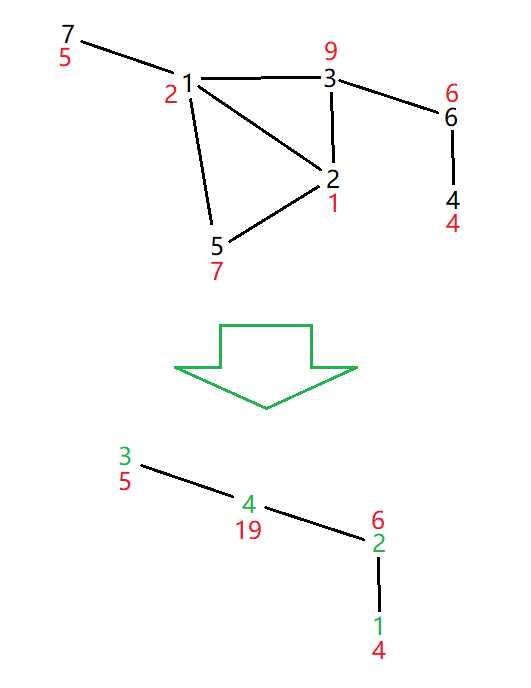
黑色为点编号,红色为权值,绿色为新点的色块号
7 8 |
有向图
骨骼清奇的算法,和上面的模板不一样
是个离线算法,比较无力
必须保证处理的边严格按照父节点指向子节点,不然还要转化一下
了解一下就好啦。。
在知道所有的要查询的点和所有点的父子关系后,进行一遍搜索,得出答案
具体怎么弄的我记不太清楚了,时隔四个月

代码如下:
C++:
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int MAXN=10010,MAXM=10010; 6 int father[MAXN],n,q; 7 bool visit[MAXN]; 8 vector<int> query[10010]; 9 10 int u,v,numedge=1,heads[MAXN]; 11 struct EDGE{ 12 int next,to; 13 }edge[MAXM]; 14 inline void adde(int u,int v){ 15 ++numedge; 16 edge[numedge].next=heads[u]; 17 edge[numedge].to=v; 18 heads[u]=numedge; 19 } 20 21 int pony_Connect(int x){//用父子关系连接起来的路径,我们要求的是lca,不能用路径压缩 22 if(father[x]!=x) return pony_Connect(father[x]); 23 else return x; 24 } 25 26 void dfs(int x){ 27 for(int i=heads[x];i!=0;i=edge[i].next) 28 { 29 dfs(edge[i].to); 30 father[edge[i].to]=x; 31 visit[edge[i].to]=1; 32 } 33 //一边搜,一边处理要查找的lca 34 for(vector<int>::iterator i=query[x].begin();i!=query[x].end();++i) 35 if(visit[*i]) printf("[%d] [%d] LCA : %d ",*i,x,pony_Connect(*i)); 36 } 37 38 int main(int argc,char* argv[], char* enc[]) 39 { 40 scanf("%d%d",&n,&q); 41 for(int i=1;i<=n;++i) father[i]=i; 42 for(int i=1;i<=n-1;++i){ 43 scanf("%d%d",&u,&v); 44 adde(u,v); 45 } 46 for(int i=1;i<=q;++i){ 47 scanf("%d%d",&u,&v); 48 query[u].push_back(v); 49 query[v].push_back(u); 50 } 51 52 dfs(1); 53 54 return 0; 55 }
测试数据:
|
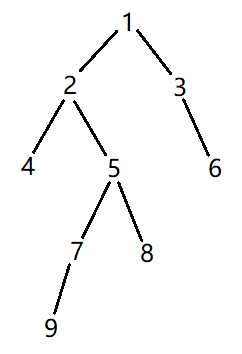
注意,实际上是有向图 这组数据有9个节点,4次查询
9 4 1 2 4 5 |
以上是关于Tarjan算法的主要内容,如果未能解决你的问题,请参考以下文章