强连通分量 寇瑟茹酒

Posted 2021-02-04 fzw1523

　　　　　　转自大佬博客  ：   https://www.cnblogs.com/nullzx/p/6437926.html

　　　　　　　　　　

1. 定义

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

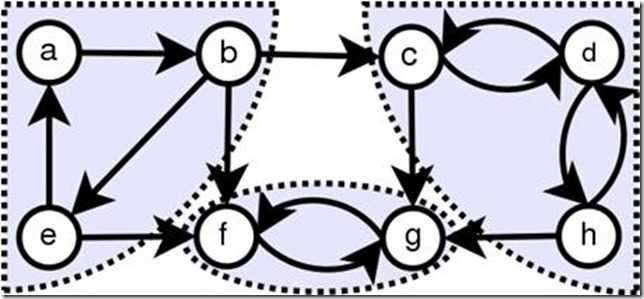
连通分量：在无向图中，即为连通子图。

上图中，总共有四个连通分量。顶点A、B、C、D构成了一个连通分量，顶点E构成了一个连通分量，顶点F，G和H，I分别构成了两个连通分量。

 

 

 

 

 

 

 

 

 

 

 

强连通分量：有向图中，尽可能多的若干顶点组成的子图中，这些顶点都是相互可到达的，则这些顶点成为一个强连通分量。

上图中有三个强连通分量，分别是a、b、e以及f、g和c、d、h。

 

2. 连通分量的求解方法

对于一个无向图的连通分量，从连通分量的任意一个顶点开始，进行一次DFS，一定能遍历这个连通分量的所有顶点。所以，整个图的连通分量数应该等价于遍历整个图进行了几次（最外层的）DFS。一次DFS中遍历的所有顶点属于同一个连通分量。

下面我们将介绍有向图的强连通分量的求解方法。

3. Kosaraju算法的基本原理

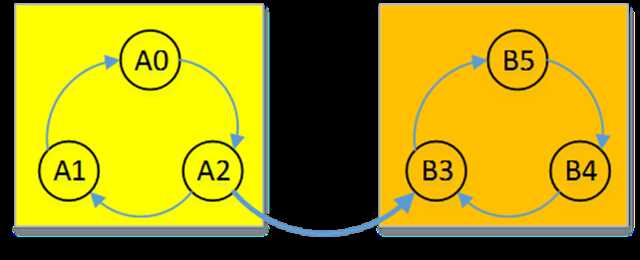
我们用一个最简单的例子讲解Kosaraju算法

显然上图中有两个强连通分量，即强连通分量A和强连通分量B，分别由顶点A0-A1-A2和顶点B3-B4-B5构成。每个连通分量中有若干个可以相互访问的顶点（这里都是3个），强连通分量与强连通分量之间不会形成环，否则应该将这些连通分量看成一个整体，即看成同一个强连通分量。

我们现在试想能否按照无向图中求连通分量的思路求解有向图的强连通分量。我们假设，DFS从强连通分量B的任意一个顶点开始，那么恰好遍历整个图需要2次DFS，和连通分量的数量相等，而且每次DFS遍历的顶点恰好属于同一个连通分量。但是，我们若从连通分量A中任意一个顶点开始DFS，就不能得到正确的结果，因为此时我们只需要一次DFS就访问了所有的顶点。所以，我们不应该按照顶点编号的自然顺序（0,1,2，……）或者任意其它顺序进行DFS，而是应该按照被指向的强连通分量的顶点排在前面的顺序进行DFS。上图中由强连通分量A指向了强连通分量B。所以，我们按照

B3, B4, B5, A0, A1, A2

的顺序进行DFS，这样就可以达到我们的目的。但事实上这样的顺序太过严格，我们只需要保证被指向的强连通分量的至少一个顶点排在指向这个连通分量的所有顶点前面即可，比如

B3, A0, A1, A2, B4, B5

B3排在了强连通分量A所有顶点的前面。

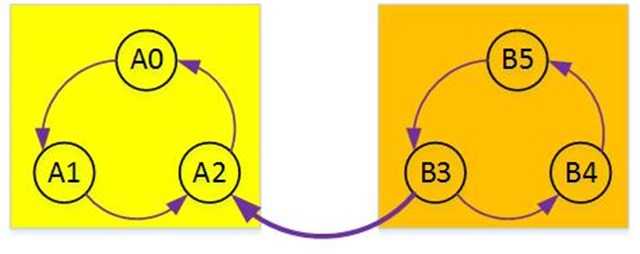
现在我们的关键问题就是如何得到这样一个满足要求的顶点顺序，Kosaraju给出了这解决办法：对原图取反，然后从反向图的任意节点开始进行DFS的逆后序遍历，逆后序得到的顺序一定满足我们的要求。

DFS的逆后序遍历是指：如果当前顶点未访问，先遍历完与当前顶点相连的且未被访问的所有其它顶点，然后将当前顶点加入栈中，最后栈中从栈顶到栈底的顺序就是我们需要的顶点顺序。

 

上图表示原图的反向。

我们现在进行第一种假设：假设DFS从位于强连通分量A中的任意一个节点开始。那么第一次DFS完成后，栈中全部都是强连通分量A的顶点，第二次DFS完成后，栈顶一定是强连通分量B的顶点。保证了从栈顶到栈底的排序强连通分量B的顶点全部都在强连通分量A顶点之前。

我们现在进行第二种假设：假设DFS从位于强连通分量B中的任意一个顶点开始。显然我们只需要进行一次DFS就可以遍历整个图，由于是逆后续遍历，那么起始顶点一定最后完成，所以栈顶的顶点一定是强连通分量B中的顶点，这显然是我们希望得到的顶点排序的结果。

上面使用了最简单的例子说明Kosaraju算法的原理，对于有多个强连通分量，连接复杂的情况，仍然适用。大家可以自行举例验证。

综上可得，不论从哪个顶点开始，图中有多少个强连通分量，逆后续遍历的栈中顶点的顺序一定会保证：被指向的强连通分量的至少一个顶点排在指向这个连通分量的所有顶点前面。所以，我们求解强连通分量的步骤可以分为两步：

（1）对原图取反，从任意一个顶点开始对反向图进行逆后续DFS遍历

（2）按照逆后续遍历中栈中的顶点出栈顺序，对原图进行DFS遍历，一次DFS遍历中访问的所有顶点都属于同一强连通分量。

4. 求解连通分量和强连通分量的代码实现

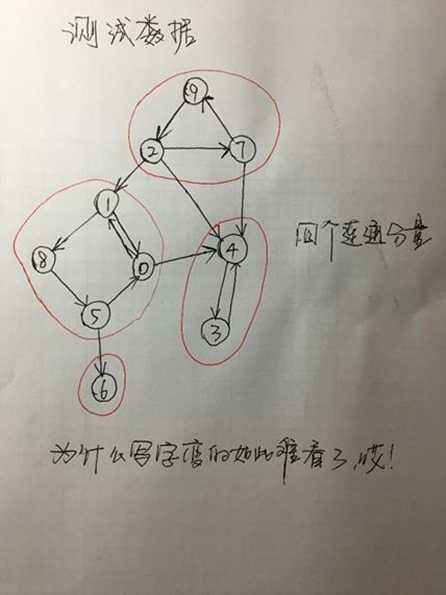
测试数据

10 15 0 1 0 4 1 0 1 8 2 1 2 4 2 7 3 4 4 3 5 0 5 6 7 9 7 4 8 5 9 2

运行结果

图的表示 0 : 1 4 1 : 0 8 2 : 1 4 7 3 : 4 4 : 3 5 : 0 6 6 : 7 : 9 4 8 : 5 9 : 2 连通分量数： 4 和顶点 0 共属于同一个连通分量的顶点 0 1 5 8 和顶点 3 共属于同一个连通分量的顶点 3 4 和顶点 9 共属于同一个连通分量的顶点 2 7 9 和顶点 6 共属于同一个连通分量的顶点 6