No more tricks, Mr Nanguo HDU - 3292（pell + 矩阵快速幂）

Posted 2021-02-04 wtsruvf

 

No more tricks, Mr Nanguo

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 576    Accepted Submission(s): 390

Problem Description

Now Sailormoon girls want to tell you a ancient idiom story named “be there just to make up the number”. The story can be described by the following words.
In the period of the Warring States (475-221 BC), there was a state called Qi. The king of Qi was so fond of the yu, a wind instrument, that he had a band of many musicians play for him every afternoon. The number of musicians is just a square number.Beacuse a square formation is very good-looking.Each row and each column have X musicians.
The king was most satisfied with the band and the harmonies they performed. Little did the king know that a member of the band, Nan Guo, was not even a musician. In fact, Nan Guo knew nothing about the yu. But he somehow managed to pass himself off as a yu player by sitting right at the back, pretending to play the instrument. The king was none the wiser. But Nan Guo‘s charade came to an end when the king‘s son succeeded him. The new king, unlike his father, he decided to divide the musicians of band into some equal small parts. He also wants the number of each part is square number. Of course, Nan Guo soon realized his foolish would expose, and he found himself without a band to hide in anymore.So he run away soon.
After he leave,the number of band is Satisfactory. Because the number of band now would be divided into some equal parts,and the number of each part is also a square number.Each row and each column all have Y musicians.

 

 

Input

There are multiple test cases. Each case contains a positive integer N ( 2 <= N < 29). It means the band was divided into N equal parts. The folloing number is also a positive integer K ( K < 10^9).

 

 

Output

There may have many positive integers X,Y can meet such conditions.But you should calculate the Kth smaller answer of X. The Kth smaller answer means there are K – 1 answers are smaller than them. Beacuse the answer may be very large.So print the value of X % 8191.If there is no answers can meet such conditions,print “No answers can meet such conditions”.

 

 

Sample Input

2 999888 3 1000001 4 8373

 

 

Sample Output

7181 600 No answers can meet such conditions

 

 

Author

B.A.C

 

 

Source

2010 “HDU-Sailormoon” Programming Contest

 

 

Recommend

lcy

 

pell方程的的入门题

求第k大

先求特解 然后根据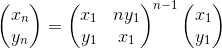

用矩阵快速幂就好了

 

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#include <bitset>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define rb(a) scanf("%lf", &a)
#define rf(a) scanf("%f", &a)
#define pd(a) printf("%d
", a)
#define plld(a) printf("%lld
", a)
#define pc(a) printf("%c
", a)
#define ps(a) printf("%s
", a)
#define MOD 8191
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = 10010, INF = 0x7fffffff;
int tot = 1;
struct Matrix
{
    LL v[110][110];
    Matrix()
    {
        memset(v, 0, sizeof(v));
    }
    Matrix operator *(const Matrix B) 
    {
        int i, j, k;
        Matrix C;
        for(i = 0; i <= tot; i ++)
            for(j = 0; j <= tot; j ++)
                for(k = 0; k <= tot; k ++)
                {
                    C.v[i][j] = (C.v[i][j] + v[i][k] * B.v[k][j]) % MOD;
                }
        return C;
    }
};

Matrix mtPow(Matrix A, int k) 
{
    int i;
    Matrix B;
    for(i = 0; i <= tot; i ++)
    {
        B.v[i][i] = 1;
    }
    while(k)
    {
        if(k & 1) B = B * A;
        A = A * A;
        k >>= 1;
    }
    return B;
}

int main()
{
    LL n, k;
    while(cin >> n >> k)
    {
        LL t = sqrt(n);
        if(t * t == n)
        {
            cout << "No answers can meet such conditions" << endl;
            continue;
        }

        LL x, y = 1;
        while(1)
        {
            x = sqrt(n * y * y + 1);
            if(x * x == n * y * y + 1) break;
            y++;
        }
        Matrix A;
        A.v[0][0] = A.v[1][1] = x % MOD;
        A.v[0][1] = (n * y) % MOD, A.v[1][0] = y % MOD;
        Matrix B = mtPow(A, k - 1);
        cout << ((B.v[0][0] * x) % MOD + (B.v[0][1] * y) % MOD) % MOD << endl;

    }


    return 0;
}