浅谈线段树

Posted 2021-02-04 bcoier

一、概念

线段树，在各个节点保存一条线段

可以高效解决连续区间的修改查询问题

由于二叉结构的特性

它每次操作能保持每个操作的复杂度为O(logn)

由于是一棵二叉树

每个节点的信息都会被logn个左右的节点记录

所以空间消耗一般较大（一般是4*n）

二、操作

1、预处理

我们先考虑节点个数是2的n次方的一段区间

在这种情况下

线段树是一棵满二叉树

所以它每个非叶子结点都有两个儿子

这里叫做左儿子和右儿子

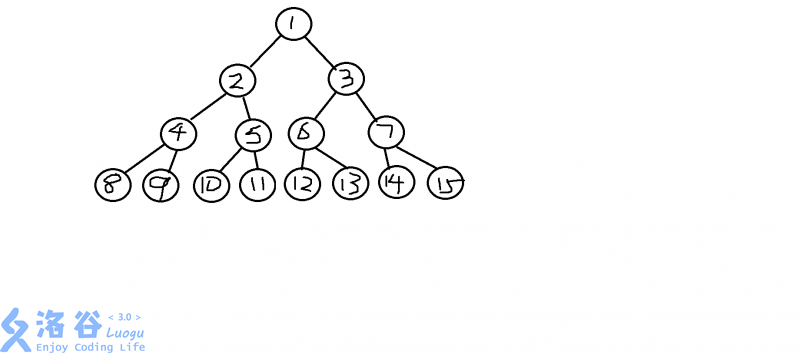
图好像有点丑

我们先来分析下线段树的一些性质

观察这张图不难发现

每一个节点的左儿子就是这个节点的编号乘以二

右儿子也是这个点的编号乘以二再加一

相反，如果我们要寻找一个节点的父亲节点

只需要将节点标号除以二即可

再进行推广，发现即使节点数不是2的n次方

仍然可以用上述方法查询左右儿子或者是父亲节点

所以查询操作如下：

#define ls(k) (k)*2//找左儿子
#define rs(k) (k)*2+1//找右儿子

我们也可以用位运算来优化，思路如下

#define ls(k) (k)<<1
#define rs(k) (k)<<1|1

接下来就考虑建树

建树的操作就是将一段区间不断二分

直到遍历到叶子节

到叶子节点后，我们可以开始维护我们想要维护的东西

如最大值、最小值、区间和等

之后，我们再回溯上去，把其他节点也更新

具体代码实现如下：

inline void build(int k,int l,int r)
{
    if(l==r)
    {
        sum[k]=a[l];//区间和
        //min[k]=a[l];//区间最小值
        //max[k]=a[l];//区间最大值
        return;
    }
    int mid=(l+r)>>1;
    build(ls(k),l,mid);//遍历左儿子
    build(rs(k),mid+1,r);//遍历右儿子
    sum[k]=sum[ls(k)]+sum[rs(k)];//区间和
    //区间最小于区间最大代码类似，在此不做赘述
}

2、区间修改

这道题需要我们维护的修改操作是区间加

我认为修改操作和建树类似

也是先不断二分

如果修改的区间包括目前遍历的区间

那就回溯，否则就继续二分

具体代码实现如下：

inline void ad(int k,int l,int r,int v)
{
    add[k]+=v;//懒标记，之后也会详细说明
    sum[k]+=v*(r-l+1);
}//把被包括的区间进行操作
inline void ADD(int k,int l,int r,int x,int y,int v)
{
    if(l>=x&&r<=y)
    {
        ad(k,l,r,v);
        return;
    }//如果包括遍历区间，就直接加
    int mid=(l+r)>>1;
    pushdown(k,l,r,mid);//标记下传，之后会细讲
    if(x<=mid)
    {
        ADD(ls(k),l,mid,x,y,v);
    }
    if(mid<y)
    {
        ADD(rs(k),mid+1,r,x,y,v);
    }
    sum[k]=sum[ls(k)]+sum[rs(k)];
    //和建树操作类似
}

3、区间查询

这道题是要我们维护区间和

那么和区间修改一样

不断二分，如果修改的区间包括目前遍历的区间

那就返回这一区间的区间和

然后回溯

把询问到的叶子节点或被包含的区间相加就是答案

具体代码如下：

inline int check(int k,int l,int r,int x,int y)
{
    if(l>=x&&r<=y)
    {
        return sum[k];
    }//修改的区间包括目前遍历的区间，就返回这一区间的区间和
    int mid=(l+r)>>1,ans=0;
    pushdown(k,l,r,mid);//标记下传
    if(x<=mid)
    {
        ans=check(ls(k),l,mid,x,y);
    }
    if(mid<y)
    {
        ans+=check(rs(k),mid+1,r,x,y);
    }//把左右部分的值全都加上
    return ans;
}

4、懒标记和标记下传

线段树的优点不在于全记录（那样复杂度就不是O(logn)了）

而在于传递式记录

其实线段树的维护还有另一种方法，叫做标记永久化

但是由于作者太蒟，所以在此就不作介绍了

有兴趣的话可以来切一下这些题目

1st ~ 2nd

标记下传的本质也和前面操作一样

如果操作一段区间,那就只要记录在这段区间公共祖先节点上（单点其实也是区间，只不过长度为1罢了）

当我们需要查询子节点的信息的时候我们再进行更新

也就是当我们不需要查询的时候，就下传标记

要用的时候就使用标记,再将使用的标记清零

我们采用上述方式

就只需要在每次操作时下传一次标记即可

大大节省了时间

这种不仅简单粗暴，还剩时间的方法,被称为————懒标记（lazy tag）

但是在访问任何一个节点时

都需要保证该节点的祖先标记都被清空

这样才能保证正确性

具体实现如下：

inline void pushdown(int k,int l,int r,int mid)
{
    if(!add[k])
    {
        return;
    }
    ad(ls(k),l,mid,add[k]);
    ad(rs(k),mid+1,r,add[k]);
    add[k]=0;
} 

三、代码实现

#include<bits/stdc++.h>
using namespace std;
#define ls(k) (k)<<1
#define rs(k) (k)<<1|1
#define int long long
#define maxn 100005
int n,m,a[maxn],x,y,z,b,sum[maxn*4],add[maxn*4];
inline void build(int k,int l,int r)
{
    if(l==r)
    {
        sum[k]=a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(ls(k),l,mid);
    build(rs(k),mid+1,r);
    sum[k]=sum[ls(k)]+sum[rs(k)];
}
inline void ad(int k,int l,int r,int v)
{
    add[k]+=v;
    sum[k]+=v*(r-l+1);
}
inline void pushdown(int k,int l,int r,int mid)
{
    if(!add[k])
    {
        return;
    }
    ad(ls(k),l,mid,add[k]);
    ad(rs(k),mid+1,r,add[k]);
    add[k]=0;
} 
inline void ADD(int k,int l,int r,int x,int y,int v)
{
    if(l>=x&&r<=y)
    {
        ad(k,l,r,v);
        return;
    }
    int mid=(l+r)>>1;
    pushdown(k,l,r,mid);
    if(x<=mid)
    {
        ADD(ls(k),l,mid,x,y,v);
    }
    if(mid<y)
    {
        ADD(rs(k),mid+1,r,x,y,v);
    }
    sum[k]=sum[ls(k)]+sum[rs(k)];
}
inline int check(int k,int l,int r,int x,int y)
{
    if(l>=x&&r<=y)
    {
        return sum[k];
    }
    int mid=(l+r)>>1,ans=0;
    pushdown(k,l,r,mid);
    if(x<=mid)
    {
        ans=check(ls(k),l,mid,x,y);
    }
    if(mid<y)
    {
        ans+=check(rs(k),mid+1,r,x,y);
    }
    return ans;
}
signed main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    build(1,1,n);
    while(m--)
    {
        cin>>b>>x>>y;
        if(b==1)
        {
            cin>>z;
            ADD(1,1,n,x,y,z);
        }
        else
        {
            cout<<check(1,1,n,x,y)<<endl;
        }
    }
    return 0;
}