ACM(图论)——tarjan算法详解

Posted 2021-02-04 henulhy

---恢复内容开始---

tarjan算法介绍：

　　一种由Robert Tarjan提出的求解有向图强连通分量的线性时间的算法。通过变形，其亦可以求解无向图问题

　　桥：

　　割点：

　　连通分量：

　　

适用问题：

　　求解（有向图/无向图）的，桥，割点，环，回路等问题

整体思想：

　　如果我们欲要求解，桥的个数，割点的个数，环的数目，归根结底，是分析清楚一个图 有几个 环，每个环包含哪些节点，那些边。

　　而 tarjan算法就是做的这件事情，通过dfs遍历每一条边和节点，算出有几个环，每个环中有哪些节点。那么是如何做的呢，整体上我们可以这么理解。

　　首先定义两个 数组 dfn[i]  low[i]  分别代表 每个节点的代号  和 每个环的代号，还有一个分析的次序 cnt变量。然后我们用dfs 深度遍历每一个顶点，每遍历一个节点 cnt++，low[i]=dfn[i]=cnt 就是说，每个节

　　点的代号代表它是第几个被我们分析的，同时low[i]=cnt 是说刚开始我们无法判断哪些节点能组成环，所以就初始化为每个节点自己是一个环，这个环的代号就是自己的代号。而当我们分析到一定程度后

　　发现，某些节点能组成一个环，再回溯，将这几个节点所属环代号改为一个统一的环代号。到最后，如果一个节点的环代号和自己的代号相等，说明他是一个割点，而如果不相等，则这个节点属于一个

　　环，并且通过环代号知道他是那个环。

思想详细分解：

　　

　　这里我们需要对一些变量重新定义其在代码中的含义，之前所说只是理解上的含义。

　　dfn[i]:节点 i dfs的次序

　　low[i]: 节点 i 所在环中 所有节点中最小的 dfn[i]。

 　　vis[i]:这个节点是否被遍历过，遍历过为1，否则为0

　　cnt:遍历次数

　　a[60]:用来存储图的 vector。

 

　　-------------------------------------------------------------------------------------------------详细的分步分析------------------------------------------------------------------------------------------------------------------------------------------------------

 

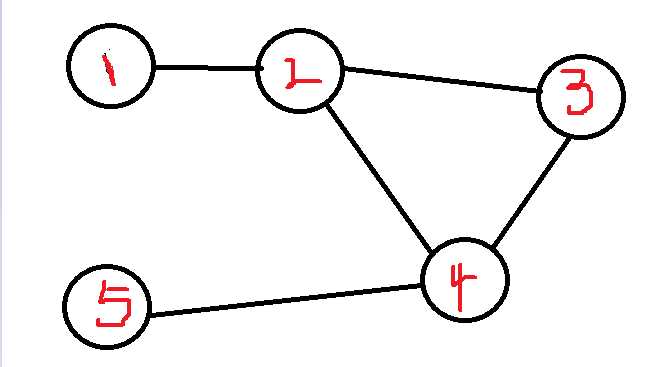
 　　假如我们从  节点1  开始遍历， low[1]=dfn[1]=cnt=1; 然后遍历他的下一个节点，如果下一个节点曾经遍历过，说明这里能形成一个环，如果没便利过，就接着往下遍历。下一个是 节点2

　　low[2]=dfn[2]=cnt=2; 再下一个是 节点3  low[3]=dfn[3]=cnt=3 , 然后  low[4]=dfn[4]=cnt =4,直到 4 的下一个节点可以到 节点2 曾经便利过 ，因此节点2到节点4之间会有一个环，接着我们向后回溯

　　使 low[4]=min(low[4],low[2])=2   low[3]=min(low[3],low[4])=2   low[2]=min(low[2],low[3])=2  low[1]=min(low[1],low[2])=1, 我们就会发现 节点2 ，节点3 ，节点4，的low与dfn就不一样了，且low都等于2，说明

　　他们三个组成了一个环，然后接着向下遍历 节点5 ，没有被遍历过，所以low[5]=dfn[5]=cnt=5;

　　至此 整体上 low[2]=low[3]=low[4]=2     low[1]=dfn[1]=1     low[5]=dfn[5]=5; 所以，这个图中有那几个群 ，群里有哪些节点，有哪些是割点，桥等 都一目了然了。

　　下面是详细的代码

　　求一个无向图的所有桥的个数，先输入两个数 n个节点，m条边。再输入 m对 数代表边的两个节点。

 

代码示例：

　　

#include <bits/stdc++.h>

using namespace std;
vector<int> a[60];
int dfn[60];
int low[60];int vis[60];
int cnt=1;
int dig=0;
//这里是tarjan代码模板核心
void tarjan(int w,int u){
    vis[u]=1;
    low[u]=dfn[u]=(cnt++);
    for(int i=0;i<a[u].size();i++){
        int v = a[u][i];
        if(v==w) continue;//因为是无向图，防止向后返回去遍历
        if(vis[v]!=1) tarjan(u,v);//没有便利过，就接着向下遍历，直到找到后，再执行下面的代码，也就是回溯。
        if(vis[v]==1) low[u]=min(low[u],low[v]);
    }
    if(low[u]==dfn[u]){
        dig++;
    }
}
void init(){
　　//初始化函数
    memset(dfn,0,sizeof dfn);
    memset(low,0,sizeof low);
    memset(vis,0,sizeof vis);
    memset(sp,0,sizeof sp);
}
int main()
{
    int n,m;
    cin>>n>>m;
    init();
    for(int i=0;i<m;i++){
        int k1,k2;
        cin>>k1>>k2;
        a[k1].push_back(k2);
        a[k2].push_back(k1);
    }
    tarjan(1,1);
    cout<<dig-1<<endl;
    return 0;
}

 

---恢复内容结束---