第04周-多变量线性回归

Posted 2021-02-04 jiqima

4.1多维特征

多维特征长这个样子：

   

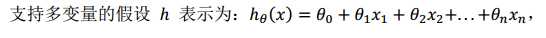
进一步的，我们为让公式简化，引入x0=1，这样的话，公式就变成下面这个样子：

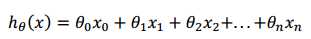
进一步的简化，可以表示为：

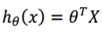
4.2多变量梯度下降

首先，构建多变量线性回归的代价函数：

   

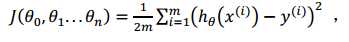
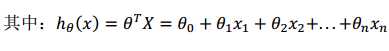
那么我们的目标就成功的转化为了：求取使代价函数最小的一系列参数。

那么多变量线性回归的批量梯度下降算法可以表示为：

如此循环，知道收敛。

python代码示例为：

4.3梯度下降法实践

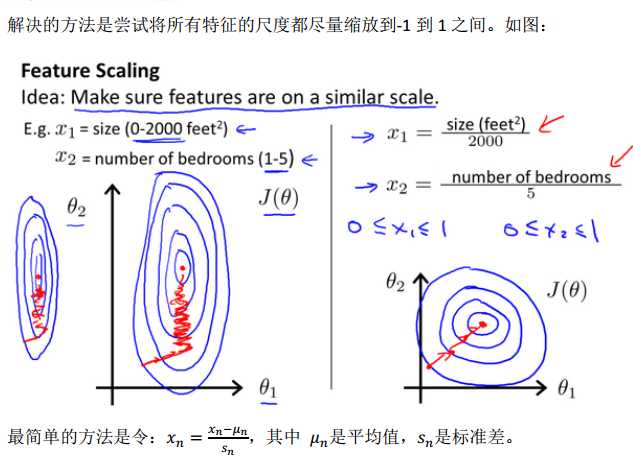
1-特征缩放

所谓的特征缩放，其实就是归一化，也可以说成是在统一量纲。

2-学习率

梯度下降算法的每次迭代受到学习率的影响，如果学习率a过小，则收敛较慢，如果学习率较大，则可能会越过局部最小值导致无法收敛。

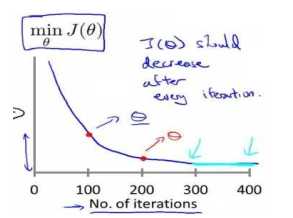
通常可以尝试的学习率为a=0.01，0.03,0.1,0.3,1,3,10

4.5特征和多项式回归

房价预测问题

线性回归并不适用于所有数据，比如二次方模型、三次方模型。

当然，我们也可以这样做：

4.6正规方程

除了使用梯度下降，对于某些线性回归问题，珍贵方程方法是更好的解决方案。如：

   

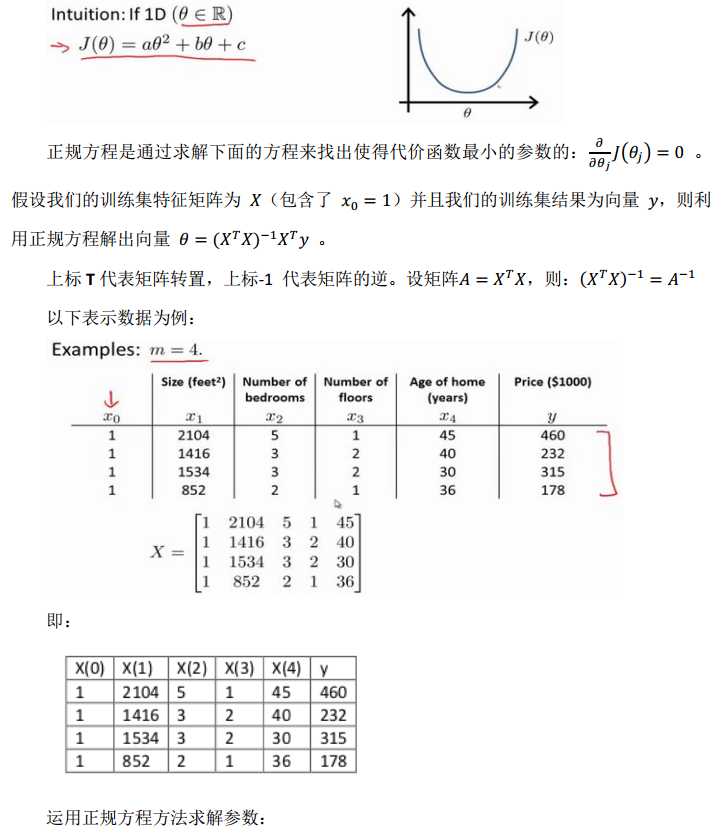
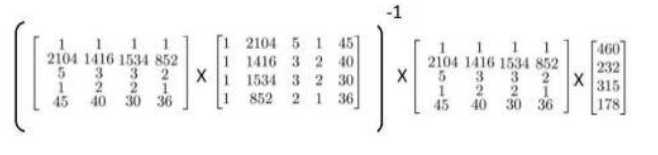
• 对于不可逆的矩阵，正规方程方法是不适用的。
• 但是大部分情况下式可逆的。
• 不可逆又叫做奇异。

梯度下降与正规方程的对比：

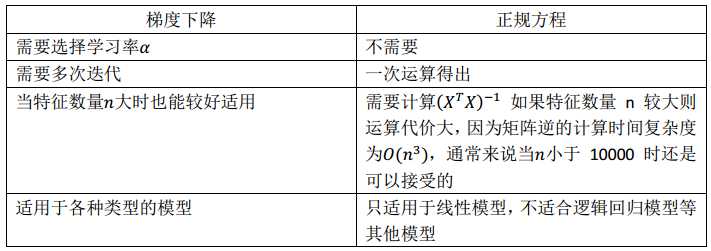
正规方程的python实现：

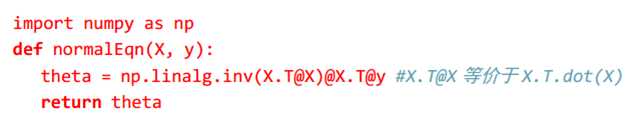
4.7正规方程及不可逆性

（待补充）