[Luogu P3157][CQOI2011]动态逆序对 (树套树)

Posted 2021-02-03 goldenpotato

题面

传送门：[CQOI2011]动态逆序对

---

Solution

一开始我看到pty巨神写这套题的时候，第一眼还以为是个SB题：这不直接开倒车线段树统计就完成了吗？

然后冷静思考了一分钟，猛然发现单纯的线段树并不能解决这个问题，好像还要在外面再套上一颗树。

这就很shit了。你问我资磁不资磁树套树，我是不资磁的，树套树是暴力数据结构，我能资磁吗？

很不幸，昨天现实狠狠地打了我一脸：时间不够开新坑的，不切题又浑身难受，找了半天题，还是把这道题拉了出来（哈，真香）

 

不扯淡了，这题还是很显然的。

考虑开倒车，我们一个一个往里面加树，然后统计一下这个数能对当前的数列有多少贡献，贡献很容易想到：我们只需要找到在他后面比他小的数以及在他前面比他大的数就好。

然后本蒟蒻写了个蜜汁线段树套splay。

时间复杂度是$O(n*log^2n)$，空间复杂度为$O(n*logn)$。理论上应该能过

可惜现实非常苦感：

 

 

.....

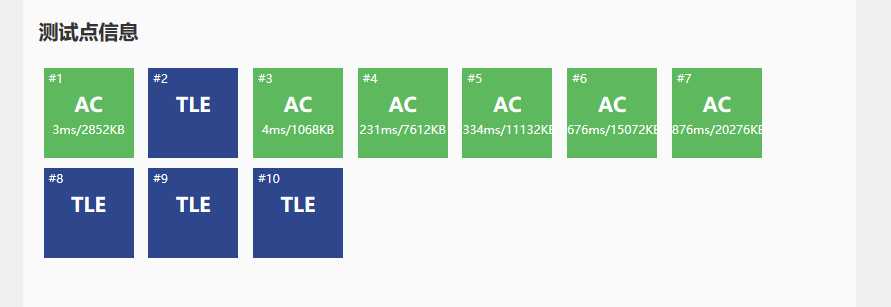
那咋搞啊。

那我上个线段树套权值线段树吧

然后又码了半个小时。

时空复杂度均为$O(n*log^2n)$ (这明显要MLE啊，问题是题解蜜汁能过)

可惜现实依旧苦感：

 

难道，改数据了？

接着，我copy了一发题解，交上去，A掉了.......

到目前为止，我还是想不通为啥开同样的数组，他A了，我T了。难道说他外层套的树状数组可以有效减少空间的消耗？

想不通，还请个位dalao赐教。

---

Code （并不能A）

线段树套splay：

#include<iostream>
#include<cstdio>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c==‘-‘) f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-‘0‘;c=getchar();}
    return x*f;
}
const int N=100000+1000;
struct TreeInTree
{
    #define mid ((now_l+now_r)>>1)
    #define lson (now<<1)
    #define rson (now<<1|1)
    #define root son[r][1]
    static const int M=N*25;
    int fa[M],son[M][2],size[M],cnt[M],num[M],to;
    inline void update(int x) 
    {
        size[x]=size[son[x][0]]+size[son[x][1]]+cnt[x];
    }
    inline void rotate(int x,int type)
    {
        int y=fa[x],z=fa[y];
        son[z][y==son[z][1]]=x,fa[x]=z;
        son[y][!type]=son[x][type],fa[son[x][type]]=y;
        son[x][type]=y,fa[y]=x;
        update(y),update(x);
    }
    void splay(int x,int to)
    {
        while(fa[x]!=to)
        {
            if(x==son[fa[x]][fa[x]==son[fa[fa[x]]][1]] and fa[fa[x]]!=to)
                rotate(fa[x],x==son[fa[x]][0]);
            rotate(x,x==son[fa[x]][0]);
        }
    }
    void Insert(int w,int r)
    {
        if(root==0)
        {
            root=++to,fa[root]=r;
            num[root]=w,update(root);
            return;
        }
        int now=root,last=root;
        while(now!=0)
            last=now,now=son[now][w>num[now]];
        now=++to,fa[now]=last,son[last][w>num[last]]=now;
        num[now]=w,update(now);
        splay(now,r);
    }
    int Query1(int x,int r)
    {
        int now=root,ans=0;
        while(now!=0)
        {
            if(num[now]>=x)
                now=son[now][0];
            else
            {
                if(num[now]>num[ans]) ans=now;
                now=son[now][1];
            }
        }
        if(ans==0) return 0;
        splay(ans,r);
        return size[son[ans][0]]+cnt[ans];
    }
    int Query2(int x,int r)
    {
        int now=root,ans=0;
        num[0]=0x3f3f3f3f;
        while(now!=0)
        {
            if(num[now]>x)
            {
                if(num[now]<num[ans]) ans=now;
                now=son[now][0];
            }
            else
                now=son[now][1];
        }
        num[0]=0;
        if(ans==0) return 0;
        splay(ans,r);
        return size[son[ans][1]]+cnt[ans];
    }
    int t[N<<2];
    void Build(int now,int now_l,int now_r)
    {
        t[now]=++to;
        if(now_l==now_r) return;
        Build(lson,now_l,mid);
        Build(rson,mid+1,now_r);
    }
    inline void Insert2(int x,int w,int now,int now_l,int now_r)
    {
        Insert(w,t[now]);
        if(now_l!=now_r)
        {
            if(x<=mid)    Insert2(x,w,lson,now_l,mid);
            else Insert2(x,w,rson,mid+1,now_r);
        }
    }
    int Query3(int l,int r,int w,int type,int now,int now_l,int now_r)
    {
        if(now_l>=l and now_r<=r)
        {
            if(type==1) return Query1(w,t[now]);
            else return Query2(w,t[now]);
        }
        int sum=0;
        if(l<=mid) sum+=Query3(l,r,w,type,lson,now_l,mid);
        if(r>mid) sum+=Query3(l,r,w,type,rson,mid+1,now_r);
        return sum;
    }
    #undef mid
    #undef lson
    #undef rson
}tit;
int n,m,p[N],q[N],unOK[N];
long long ans[N];
int main()
{    
    freopen("3157.in","r",stdin);
    freopen("3157.out","w",stdout);
    
    int t=clock();
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        p[read()]=i;
    for(int i=1;i<=m;i++)
        q[i]=read(),unOK[q[i]]=true;
    
    tit.Build(1,1,n);
    for(int i=1;i<=n;i++)
        if(unOK[i]==false)
        {
            tit.Insert2(p[i],i,1,1,n);
            ans[m+1]+=tit.Query3(p[i],n,i,1,1,1,n)+tit.Query3(1,p[i],i,2,1,1,n);
        }
    for(int i=m;i>=1;i--)
    {
        tit.Insert2(p[q[i]],q[i],1,1,n);
        ans[i]=ans[i+1]+tit.Query3(p[q[i]],n,q[i],1,1,1,n)+tit.Query3(1,p[q[i]],q[i],2,1,1,n);
    }
    
    for(int i=1;i<=m;i++)
        printf("%lld
",ans[i]);
    cerr<<clock()-t<<endl;
    return 0;
}

 

线段树套权值线段树

#include<iostream>
#include<cstdio>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c==‘-‘) f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-‘0‘;c=getchar();}
    return x*f;
}
const int N=100000+1000;
int n,m,p[N],q[N],unOK[N];
long long ans[N];
struct TreeInTree
{
    #define mid ((now_l+now_r)>>1)
    #define lson (now<<1)
    #define rson (now<<1|1)
    static const int M=N*200;
    int son[M][2],num[M],to;
    inline void update(int x) 
    {
        num[x]=num[son[x][0]]+num[son[x][1]];
    }
    void Insert(int x,int now,int now_l,int now_r)
    {
        if(now_l==now_r)
        {
            num[now]++;
            return;
        }
        if(now>to) 
            cerr<<to;
        if(x<=mid)
        {
            if(son[now][0]==0) son[now][0]=++to;
            Insert(x,son[now][0],now_l,mid);
        }
        else
        {
            if(son[now][1]==0) son[now][1]=++to;
            Insert(x,son[now][1],mid+1,now_r);
        }
        update(now);
    }
    int Query1(int l,int r,int now,int now_l,int now_r)
    {
        if(l>r) return 0;
        if((now_l>=l and now_r<=r) or now==0)
            return num[now];
        int t_ans=0;
        if(l<=mid) t_ans+=Query1(l,r,son[now][0],now_l,mid);
        if(r>mid) t_ans+=Query1(l,r,son[now][1],mid+1,now_r);
        return t_ans;
    }
    int t[N<<2];
    void Build(int now,int now_l,int now_r)
    {
        t[now]=++to;
        if(now_l==now_r) return;
        Build(lson,now_l,mid);
        Build(rson,mid+1,now_r);
    }
    inline void Insert2(int x,int w,int now,int now_l,int now_r)
    {
        Insert(w,t[now],1,n);
        if(now_l!=now_r)
        {
            if(x<=mid)    Insert2(x,w,lson,now_l,mid);
            else Insert2(x,w,rson,mid+1,now_r);
        }
    }
    int Query3(int l,int r,int w,int type,int now,int now_l,int now_r)
    {
        if(now_l>=l and now_r<=r)
        {
            if(type==1) return Query1(1,w-1,t[now],1,n);
            else return Query1(w+1,n,t[now],1,n);
        }
        int sum=0;
        if(l<=mid) sum+=Query3(l,r,w,type,lson,now_l,mid);
        if(r>mid) sum+=Query3(l,r,w,type,rson,mid+1,now_r);
        return sum;
    }
    #undef mid
    #undef lson
    #undef rson
}tit;
int main()
{    
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        p[read()]=i;
    for(int i=1;i<=m;i++)
        q[i]=read(),unOK[q[i]]=true;
    
    tit.Build(1,1,n);
    for(int i=1;i<=n;i++)
        if(unOK[i]==false)
        {
            tit.Insert2(p[i],i,1,1,n);
            ans[m+1]+=tit.Query3(p[i],n,i,1,1,1,n)+tit.Query3(1,p[i],i,2,1,1,n);
        }
    for(int i=m;i>=1;i--)
    {
        tit.Insert2(p[q[i]],q[i],1,1,n);
        ans[i]=ans[i+1]+tit.Query3(p[q[i]],n,q[i],1,1,1,n)+tit.Query3(1,p[q[i]],q[i],2,1,1,n);
    }
    
    for(int i=1;i<=m;i++)
        printf("%lld
",ans[i]);
    return 0;
}