数据结构之线性表的顺序存储结构

Posted 2021-02-03 naihuangbao

1.线性表
定义：线性表是零个或多个数据元素的有限序列。
两种物理结构：顺序存储结构和链式存储结构。

2.线性表的顺序存储结构
定义：是指用一段地址连续的数据单元依次存储线性表的数据元素。说白了就是在内存中占用一块空间，然后将相同数据类型的元素依次存入。

在线性表的定义中，指出是用一段地址连续的数据单元存储线性表中的元素，由于存入的是相同类型的数据元素，所以可以使用数组来充当这段地址连续的数据单元。在实现线性表的顺序存储时，首先应该先创建这块地址连续的数据单元。

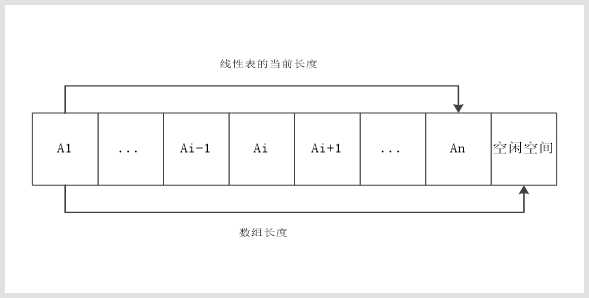
要使用数组作为载体来存储线性表，就涉及到了两个长度，一个是数组的长度，是在内存中占用的空间，应该提前定义好数组的长度即占用空间的内存大小，这个空间大小是固定不变的。且数组下标是从0开始。另一个是线性表的长度，线性表的长度是线性表中数据元素的长度，随着数据元素的插入和删除，线性表的长度是可变的。且线性表的长度是从1开始计数。

代码实现线性表的顺序存储结构的创建，插入和删除。

线性表创建实现的算法思路：
    1. 首先在内存中占用一块空间，作为一段地址连续的数据存储单元，使用一维数组来实现，即定义一个大小固定的一维数组。
    2. 创建线性表，即向数组中添加元素，添加元素的同时记录线性表的长度。

线性表i位置插入数据元素的算法思路：
    1. 既然是在线性表的i位置插入数据元素，首先需要判断i的大小是否超出线性表的长度范围。
    2. 在i位置插入数据元素，那么i位置之后的数据元素都需要向后移动一位，可以从数组末尾开始循环直到i，将相应位置的值后移一位。
    3. 将i位置的值修改为插入值。

线性表i位置删除数据元素的算法思路：
    1. 与插入的第一步相同，先判断i的大小是否超出线性表的长度范围。
    2. 在i位置删除数据元素，i位置之后的数据元素都需要向前移动一位，数组从i-1位置开始起循环至线性表末尾，将相应位置的值向前移动一位。

代码实现：

package com.java.ListInsert;
/*
 * 线性表的顺序存储结构的插入和删除
 * 数组作为线性表的载体
 * */
public class LineList {
    
           static int maxLen=20;
    static int[] arrayData=new int[maxLen];
    private static int len=0;
    
    //数组中添加元素
    public static void add(int e){
        arrayData[len]=e;
        len++;
    }
    
    //创建顺序存储结构的线性表
    public static void lineList(int length){
        if(length<maxLen){
            for(int i=0;i<length;i++){
                add(i);
            }
        }else{
            System.out.println("添加元素溢出!");
        }
    }
    
    //线性表的顺序存储结构i的位置插入元素，线性表从1开始，数组从0开始
    public static void insert(int i,int element){
        int m;
        if(i<1 || i>len){
            System.out.println("插入位置溢出!");
        }else{
            for(m=maxLen-1;m>=i;m--){
                arrayData[m]=arrayData[m-1];
            }
            arrayData[i-1]=element;
            len++;
            for(int j=0;j<arrayData.length;j++){
                System.out.print(arrayData[j]);
            }
        }
        System.out.println("");
    }
    
    //删除线性表顺序存储结构i位置的元素
    public static void delete(int i){
        int m;
        if(i<1 || i>len){
            System.out.println("删除位置出错");
        }else{
            for(m=i-1;m<maxLen-1;m++){
                arrayData[m]=arrayData[m+1];
            }
            for(int j=0;j<arrayData.length;j++){
                System.out.print(arrayData[j]);
            }
            len--;
        }
    }
    
    public static void main(String[] args){
        lineList(10);
        insert(10,5);
        delete(11);
    }
}

3.顺序存储结构的地址计算方法
存储器中的每个单元都有自己的编号，这个编号叫地址。

假设每个数据元素占用的是c个内存单元，那么第i+1个数据元素的存储单元和第i个数据元素的存储单元的位置满足如下关系：LOC(Ai+1)=LOC(Ai)+c,因此可以推出第i个数据元素的存储单元和第一个元素存储单元的位置关系：LOC(Ai)=LOC(A1)+(i-1)*c。

3.1 存取的时间复杂度分析
由上面这个公式可以轻易地推算出每个数据元素的位置地址，那么我们对于线性表中每个位置的数据元素的进行读入和取出操作的时间对于计算机而言来说都是相同的，是一个常数，用算法的时间复杂度概念来说，它的存取时间性能为O(1)，通常把具有这种特点的存储结构称为随机存取结构。

3.2 插入和删除的时间复杂度分析
最好的情况就是在表尾插入或删除一个数据元素，这时不需要移动其他数据元素，时间复杂度为O(n)。最坏的情况
是在第一个位置插入或删除一个数据元素，时间复杂度为O(n)。从所有的元素来看，位置越靠前，移动次数越多，位置越靠后，移动次数越少，平均移动次数和中间的数据元素移动的次数是相同的，为(n-1)/2。所以插入和删除的平均时间复杂度为O(n)。

4.线性表顺序存储结构的优缺点
优点：
    1. 不需要为表中元素之间的逻辑关系增加额外的存储存储空间；
    2. 可以快速地存取表中任意位置的数据元素（存取时间复杂度为O(1)）；
缺点：
    1. 插入和删除需要移动大量的数据元素（插入删除时间复杂度为O(n)）；
    2. 难以确定存储空间的容量；