二叉搜索树

Posted 2021-02-02 archer-fang

二叉搜索树（BST）有时也被叫做有序二叉树或者排序二叉树是一种特别的容器类型：是一种储存数据到内存中的数据结构。二叉树允许快速查找，添加和删除元素，而且不仅可以被用于实现动态数据集，而且在查找数据表的时候可以允许通过key来查找一个元素。
二叉查找树会保持节点的key是排好序的，因此做查找或者其他操作的时候可以使用二分法
时间复杂度O（logn）

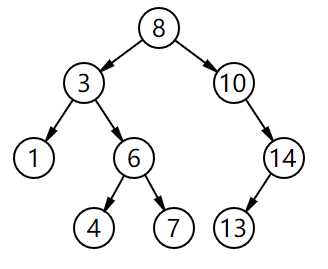
如图：左小中 中小右

BinarySearchTreeNode:

import BinaryTreeNode from ‘../BinaryTreeNode‘;
import Comparator from ‘../../../utils/comparator/Comparator‘;

export default class BinarySearchTreeNode extends BinaryTreeNode {
  /**
   * @param {*} [value] - node value.
   * @param {function} [compareFunction] - comparator function for node values.
   */
  constructor(value = null, compareFunction = undefined) {
    super(value);

    // This comparator is used to compare node values with each other.
    this.compareFunction = compareFunction;
    this.nodeValueComparator = new Comparator(compareFunction);
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  insert(value) {
    if (this.nodeValueComparator.equal(this.value, null)) {
      this.value = value;

      return this;
    }

    if (this.nodeValueComparator.lessThan(value, this.value)) {
      // Insert to the left.
      if (this.left) {
        return this.left.insert(value);
      }

      const newNode = new BinarySearchTreeNode(value, this.compareFunction);
      this.setLeft(newNode);

      return newNode;
    }

    if (this.nodeValueComparator.greaterThan(value, this.value)) {
      // Insert to the right.
      if (this.right) {
        return this.right.insert(value);
      }

      const newNode = new BinarySearchTreeNode(value, this.compareFunction);
      this.setRight(newNode);

      return newNode;
    }

    return this;
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  find(value) {
    // Check the root.
    if (this.nodeValueComparator.equal(this.value, value)) {
      return this;
    }

    if (this.nodeValueComparator.lessThan(value, this.value) && this.left) {
      // Check left nodes.
      return this.left.find(value);
    }

    if (this.nodeValueComparator.greaterThan(value, this.value) && this.right) {
      // Check right nodes.
      return this.right.find(value);
    }

    return null;
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  contains(value) {
    return !!this.find(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  remove(value) {
    const nodeToRemove = this.find(value);

    if (!nodeToRemove) {
      throw new Error(‘Item not found in the tree‘);
    }

    const { parent } = nodeToRemove;//找到要移除结点的父结点

    if (!nodeToRemove.left && !nodeToRemove.right) {
      // Node is a leaf and thus has no children.
      if (parent) {
        // Node has a parent. Just remove the pointer to this node from the parent.
        parent.removeChild(nodeToRemove);
      } else {
        // Node has no parent. Just erase current node value.
        nodeToRemove.setValue(undefined);
      }
    }
    else if (nodeToRemove.left && nodeToRemove.right) {
      // Node has two children.
      // Find the next biggest value (minimum value in the right branch)找到根节点的下一个相连结点（数值上的）
      // and replace current value node with that next biggest value.
      const nextBiggerNode = nodeToRemove.right.findMin();
      if (!this.nodeComparator.equal(nextBiggerNode, nodeToRemove.right)) {//如果右子树的最小节点和要删除的节点的右子节点不是同一个节点，那么就删掉右子树最小节点的值，给要删除节点赋值
        this.remove(nextBiggerNode.value);
        nodeToRemove.setValue(nextBiggerNode.value);
      } else {
        // In case if next right value is the next bigger one and it doesn‘t have left child如果右子树的最小节点和要删除的节点的右子节点是同一个节点，且右子树的那个结点无左孩子
        // then just replace node that is going to be deleted with the right node.
        nodeToRemove.setValue(nodeToRemove.right.value);
        nodeToRemove.setRight(nodeToRemove.right.right);
      }
    }
    else {
      // Node has only one child.
      // Make this child to be a direct child of current node‘s parent.
      /** @var BinarySearchTreeNode */
      const childNode = nodeToRemove.left || nodeToRemove.right;

      if (parent) {
        parent.replaceChild(nodeToRemove, childNode);
      } else {
        BinaryTreeNode.copyNode(childNode, nodeToRemove);
      }
    }

    // Clear the parent of removed node.
    nodeToRemove.parent = null;

    return true;
  }

  /**
   * @return {BinarySearchTreeNode}
   */
  findMin() {
    if (!this.left) {
      return this;
    }

    return this.left.findMin();
  }
}

BinarySearchTree:

 

import BinarySearchTreeNode from ‘./BinarySearchTreeNode‘;

export default class BinarySearchTree {
  /**
   * @param {function} [nodeValueCompareFunction]
   */
  constructor(nodeValueCompareFunction) {
    this.root = new BinarySearchTreeNode(null, nodeValueCompareFunction);

    // Steal node comparator from the root.
    this.nodeComparator = this.root.nodeComparator;
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  insert(value) {
    return this.root.insert(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  contains(value) {
    return this.root.contains(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  remove(value) {
    return this.root.remove(value);
  }

  /**
   * @return {string}
   */
  toString() {
    return this.root.toString();
  }
}

note:

1.BinarySearchTreeNode中remove的说明：找到要删除的结点，要删除结点的父结点，

即：

const { parent } = nodeToRemove;

然后分三种情况考虑

（1）没有左孩子也没有右孩子，如果存在父结点则，删除该节点，否则根结点置空

（2）左（this.left）右孩子(this.right)都有，找到该结点右子树最小的结点即为min进行判断

  【1】如果min!=this.right，则递归的去删除掉min所在结点，并且把min的值赋给this

   !!!【2】如果min=this.right，则this.right.left必为null，，所以把min值给this，同时，this.right=this.right.right.

（3）只有左孩子或者右孩子，如果有父结点，则用该结点的左或右孩子替换掉该结点，否则删除该结点的左或右结点，并且把该结点的左或右结点的1.值2.左孩子3.右孩子，赋值给该结点。