决策树的部分理解

Posted 2021-02-01 jcjc

决策树的部分理解

• 决策树

  • 是表示基于特征对实例进行分类的树形结构

  • 从给定的训练数据集中，依据特征选择的准则，递归的选择最优划分特征，并根据此特征将训练数据进行分割，使得各子数据集有一个更好的分类的过程

• 决策树算法的三要素：

  • 特征选择

  • 决策树生成

  • 决策树剪枝（暂时没接触到）

• 关于决策树生成：

  • 决策树的生成过程就是使用满足划分准则的特征不断的将数据集划分为纯度更高，不确定性更小的子集的过程

  • 对于当前数据集D的每一次的划分，都希望根据某特征划分之后的各子集的纯度更高，不确定性更小

• 而如何度量划分数据集前后的数据集的纯度以及不确定性呢？

  • 答案是：特征选择准则

    • 比如：信息增益，信息增益率，基尼指数

  • 特征选择准则的目的

    • 使用某特征对数据集进行划分之后，各数据子集的纯度要比划分前的数据集D的纯度高（不确定性要比划分前数据集D的不确定性低）

• 我们使用的特征选择准则是：基尼指数（CART算法---分类树）

  • 基尼指数（基尼不纯度），表示在样本集合中一个随机选中的样本被分错的概率

  • PS： 基尼指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯

  • 即：

    • 基尼指数（基尼不纯度） = 样本被选中的概率 * 样本分错的概率

  • 书中公式：

    • 

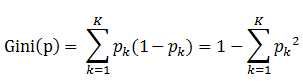
    • 说明：

    • 1、Pk表示选中的样本属于k类别的概率，则这个样本被分错的概率是（1 - Pk）

    • 2、样本集合有K个类别，一个随机选中的样本可以属于这K个类别中的任意一个，因而就K个类别的概率进行相加

  • 比如样本集合D的Gini指数

    • 假设集合中有K个类别，则：

    • 

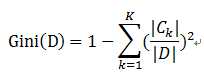
• January 8, 2019