连续子数组的最大和（基于动态规划）

Posted 2021-02-01 tianzeng

题目

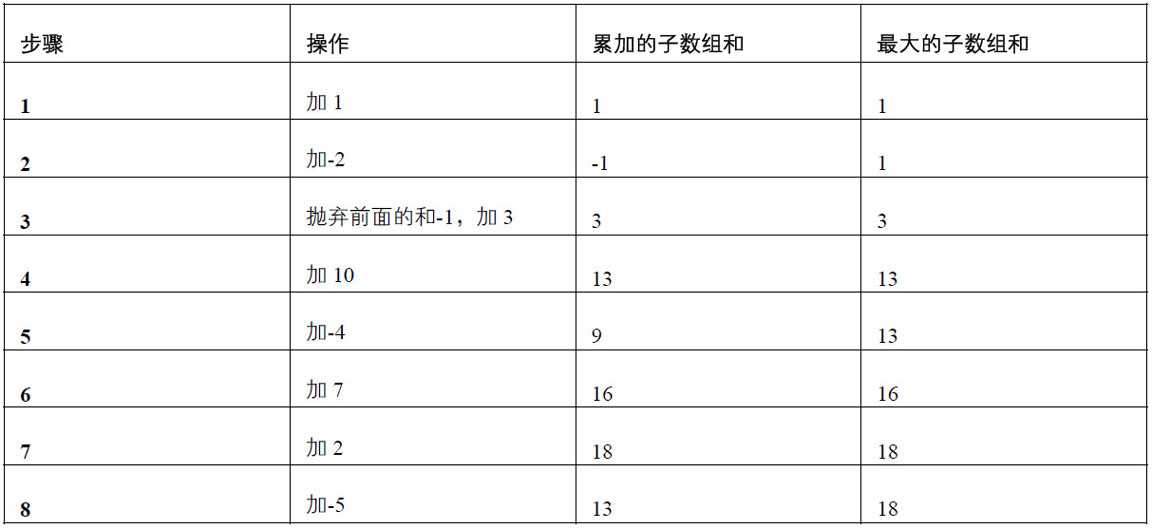
　　输入一个整型数组，数组里有正数也有负数。数组中一个或连续的多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。例如输入的数组为{1,-2,3,10,-4,7,2,-5}，和最大的子数组为{3,10,-4,7,2}，因此输出为该子数组的和18。

思路

一般解法

1. 从头到尾累加数字，保存到一个临时变量curr_sum中
2. 如果前几项的和为负，则加上此和之后比本身的值还要小，抛弃原来所计算得到的和，curr_sum从本元素开始计数 ；否则，把当前元素累加到curr_sum
3. 把curr_sum与最大值max_sum比较（max_sum保存每个连续数组的最大和）

#include <iostream>
#include <vector>
using namespace std;

class Solution
{
    public:
        int get_max_sum(const vector<int> &v);
        bool is_invalid{true}; 
};
int Solution::get_max_sum(const vector<int> &v)
{
    if(v.empty()||v.size()<0)
    {
        is_invalid=false;
        return -1;
    }
    
    is_invalid=true;
    int curr_sum=0;//当前和 
    int max_sum=0;//保存最大和 
    
    for(int i=0;i<v.size();++i)
    {
        if(curr_sum<=0)//如果前几项的和为负，则加上此和之后比本身的值还要小，数组从本元素开始计数 
            curr_sum=v[i];
        else
            curr_sum+=v[i];
            
        if(curr_sum>max_sum)
            max_sum=curr_sum;
    }
    return max_sum;
}
int main()
{
    vector<int> v{1,-2,3,10,-4,7,2,-5};
    Solution s;
    cout<<s.get_max_sum(v)<<endl;
    return 0;
}

 动态规划

　　f(i)表示以第i个数字结尾的子数组的最大和，那么只需求出max[f(i)],状态转移方程如下

      v[i],i==0||f(i-1)<0
f(i)=
      v[i]+f(i-1),i>0&&f(i-1)>0

code：

#include <iostream>
#include <vector>
using namespace std;

class Solution
{
    public:
        int get_max_sum(const vector<int> &v);
        bool is_invalid{true}; 
};
int Solution::get_max_sum(const vector<int> &v)
{
    if(v.empty()||v.size()<0)
    {
        is_invalid=false;
        return -1;
    }
    
    is_invalid=true;
    int curr_sum=0;//当前和 
    int max_sum=0;//保存最大和 
    
    for(int i=0;i<v.size();++i)
    {
        curr_sum=(curr_sum<0)?v[i]:(v[i]+curr_sum);
        max_sum=max(curr_sum,max_sum);
    }
    return max_sum;
}
int main()
{
    vector<int> v{1,-2,3,10,-4,7,2,-5};
    Solution s;
    if(s.is_invalid) 
        cout<<s.get_max_sum(v)<<endl;
    return 0;
}