多变量线性回归
Posted rinroll
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了多变量线性回归相关的知识,希望对你有一定的参考价值。
一、表达式
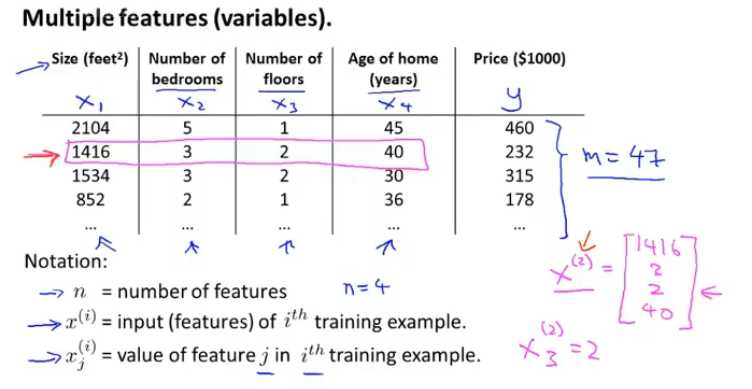
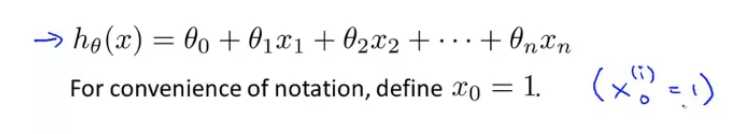
用向量的形式表示
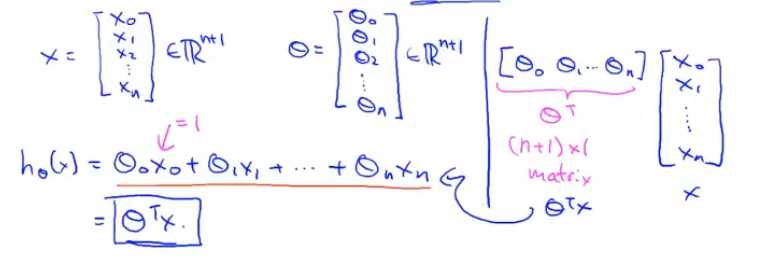
二、多元梯度下降法


规定x0(i)=1
三、多元梯度下降法演练——特征缩放

保证这些特征都处在一个相近的范围,不同特征取值在相近的范围内。
如果不在两个特征的数值范围差距很大,关于θ的关系函数会是一个又长又扁的椭圆。而这种情况下防止达不到收敛,只能进行一小步一小步的梯度计算,而且过程较复杂。
而特征数值差异较小的情况可以找到更直接的方式
那么我们可以通过归一化来降低差别
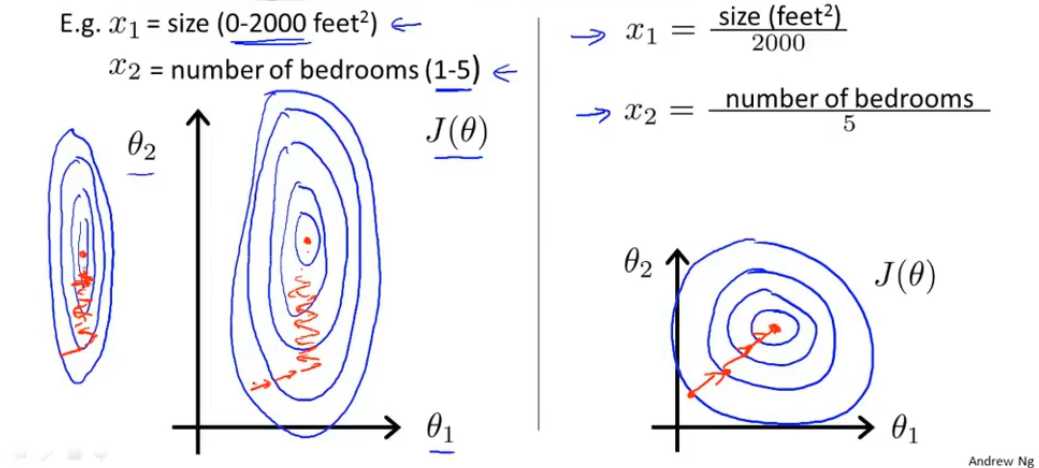
不一定要求范围一定在-1到1之间或者说不同特征范围完全相同,相近的都可以。但不能过小也不能过大
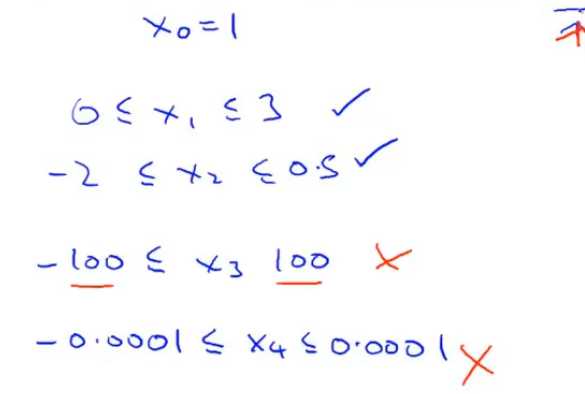
对特征缩放,除了简单的归一化,还可以进行均值归一化

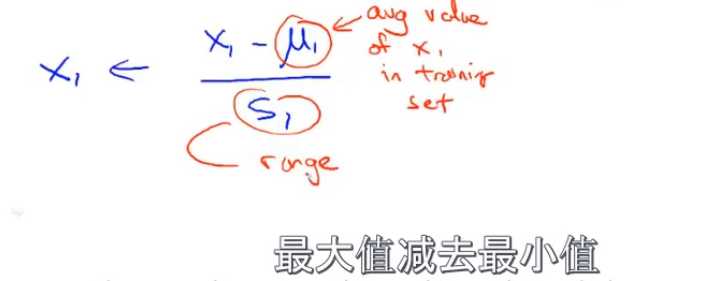
总结:特征缩放使梯度下降收敛更快,迭代次数更少。
四、多元梯度下降法——学习率α
目标:

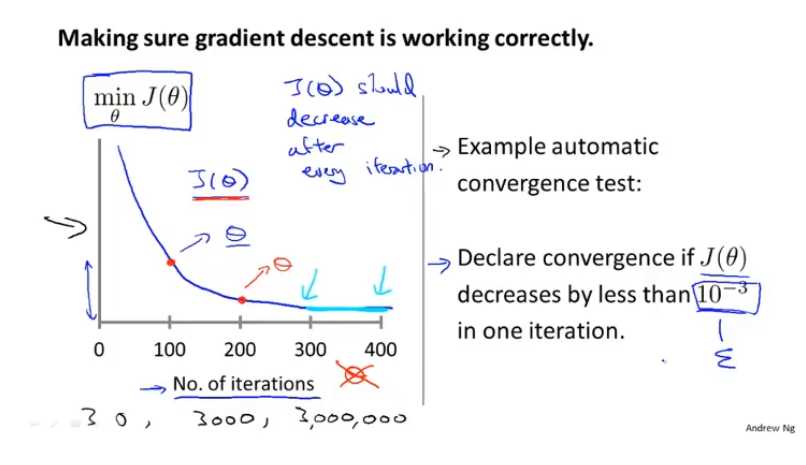
两种方法:一种看图,一种通过自动收敛测试(但这个阈值的确定十分困难)
下面这两种J(θ)都需要减少α的值
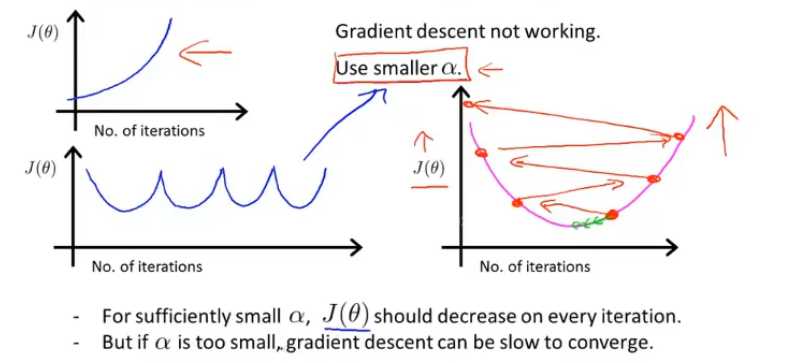

五、特征和多项式回归(线性回归拟合复杂函数或非线性函数)
定义新的特征
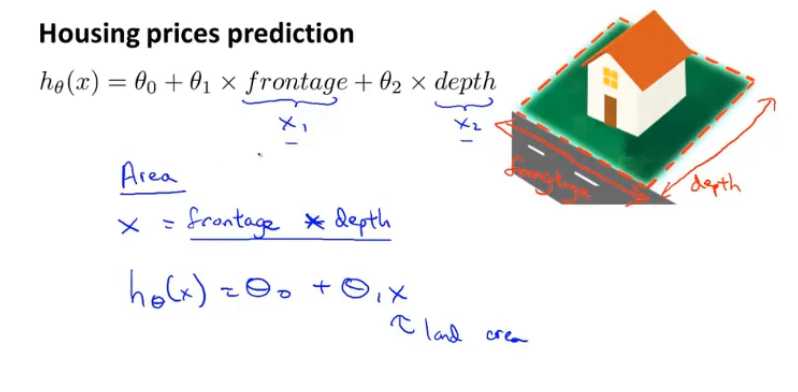
P:多项式回归——不是变量不是全都式一阶
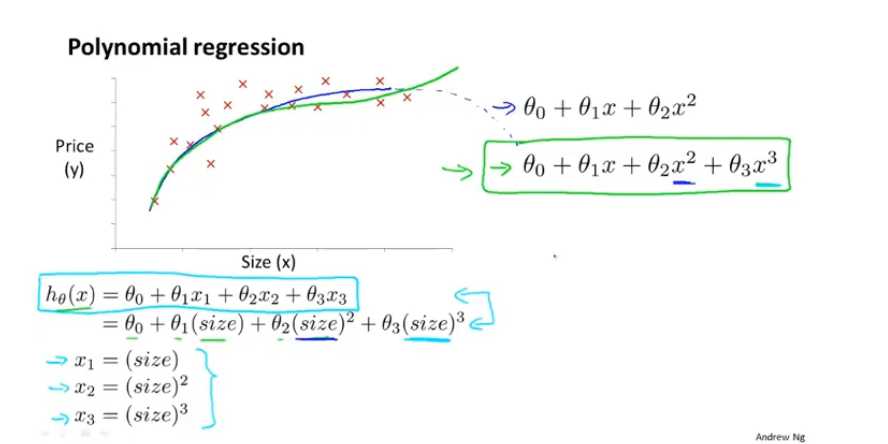
六、正规方程
未完
以上是关于多变量线性回归的主要内容,如果未能解决你的问题,请参考以下文章