OpenCV实战（14）——图像线条提取

Posted 2023-03-13 盼小辉丶

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了OpenCV实战（14）——图像线条提取相关的知识，希望对你有一定的参考价值。

OpenCV实战（14）——图像线条提取

0. 前言

基于内容的图像分析，需要从构成图像的像素集合中提取有意义的特征。轮廓、线条、区域等是基本的图像基元，可用于描述图像中包含的元素。本节将介绍如何提取重要的图像线条特征。

1. 检测图像轮廓

1.1 图像轮廓

图像轮廓包含了重要的视觉信息，可以用于描绘图像元素，因此，通常用于物体识别等计算机视觉任务。然而，简单的二值轮廓图有两个主要缺点：检测到的边缘过粗，使较小物体难以识别；更重要的是，我们通常不可能恰巧找到一个能够同时检测图像所有重要边缘并舍弃不重要边缘的阈值，Canny 算法用于解决两者之间的权衡问题。

1.2 使用 Canny 算子检测图像轮廓

Canny 算法在 OpenCV 中由 cv::Canny 函数实现，该算法需要指定两个阈值。

(1) 要将 Canny 算法应用于加载的图像，必须首先创建一个新的 cv::Mat 结构来存储结果并调用 cv::Canny 函数：

// 应用 Canny 算法
cv::Mat contours;
cv::Canny(image,    // 灰度图像
        contours,   // 输出图像
        125,        // 低阈值
        350);       // 高阈值

(2) 在测试图像上调用 Canny 算法，检测结果如下：

由于算法正常结果表示非零像素的轮廓，为了获得上示图像，我们必须反转黑白值。Canny 算子通常基于 Sobel 算子，但也可以使用其他梯度算子，关键思想是使用两个不同的阈值来确定哪些像素属于轮廓。
选择的低阈值应包括所有被认为属于重要图像轮廓的边缘像素。例如，使用指定的低阈值，并将其应用于 Sobel 算子可以得到如下边缘图：

如上图所示，道路的边缘非常明显。然而，由于使用了较低阈值，因此检测到较多的边缘。第二个阈值的作用是定义属于重要轮廓的边缘，它能够排除被视为异常值的边缘。例如，使用高阈值对应的 Sobel 边缘图如下：

上图中包含了较多破碎边缘，但其中可见的边缘均属于重要轮廓。
Canny 算法将以上两个边缘图组合在一起，以生成最佳轮廓图。其仅保留存在连续边缘路径的低阈值边缘图的边缘点，并将这些边缘点链接到属于高阈值边缘图中的边缘。因此，保留了高阈值图中的所有边缘点，同时去除了低阈值图中所有孤立的边缘点链。这是一种良好的折中解决方案，只要指定合适的阈值，就可以获得高质量的轮廓。这种基于使用两个阈值来获得二值图的策略称为滞后阈值，可用于需要从阈值操作中获得二值图的应用，但这需要以更高的计算复杂度为代价。
此外，Canny 算法还使用了其他能够提高边缘图质量的策略，在应用滞后阈值之前，移除所有梯度幅值在梯度方向上不是最大值的边缘点，得到合适边缘。由于梯度方向总是垂直于边缘，因此，方向梯度的局部最大值对应于轮廓强度最大的点。

2. 使用霍夫变换检测图像中的线条

2.1 线条的表示

在物理世界中，平面和线性结构非常常见，因此，在图像中经常可以看到直线，直线特征在物体识别和图像理解中起着重要作用。霍夫变换是一种经典算法，常用于检测图像中的特定特征。它最初用于检测图像中的线条，但也可以扩展到检测其他简单的图像结构。使用霍夫变换，使用以下等式表示线条：
$ρ=xcos(\\theta)+ysin(\\theta)$
$ρ$ 参数是直线与图像原点(左上角)之间的距离， $θ$ 是直线与直线的夹角(采用弧度制)。采用这种表示，图像中线条的角 $θ$ 介于 $0$ 到 $π$ 之间，而半径 $ρ$ 的最大值等于图像对角线长度。例如，使用以下线条：

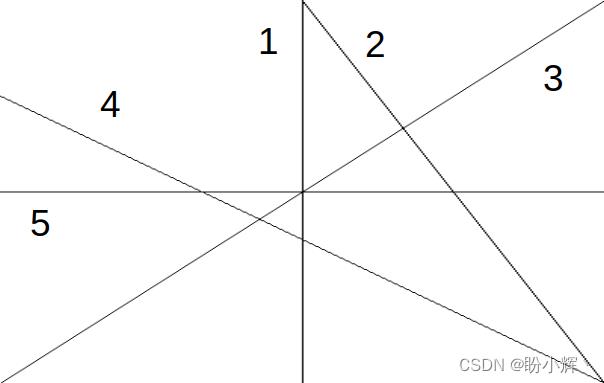
在上图中，垂直线(线 1 )的 $θ$ 角等于 $0$ ，而水平线(线 5 )的 $θ$ 值等于 $π /2$ ，线 3 的角度 $θ$ 等于 $π /4$ ，线 4 的角度大约为 $0.7 π$ 。为了能够用 $θ$ 在 $[0, π]$ 区间内表示所有可能的直线，可以将半径值设为负数，例如，线 2 的 $θ$ 值等于 $0.8 π$ ， $ρ$ 为负值。

2.2 霍夫变换检测直线

OpenCV 提供了两种用于线检测的霍夫变换实现，基本方法是 cv::HoughLines，它的输入是包含一组点(由非零像素表示)的二值图(其中一些点对齐形成线)，通常可以使用 Canny 算子获得的边缘图作为输入。cv::HoughLines 函数的输出是 cv::Vec2f 元素的向量，每个元素都是一对浮点值，表示检测到的线的参数 $(ρ, θ)$ 。

(1) 首先应用 Canny 算子得到图像轮廓：

// 应用 Canny 算法
cv::Mat contours;
cv::Canny(image,    // 灰度图像
        contours,   // 输出图像
        125,        // 低阈值
        350);       // 高阈值

(2) 使用霍夫变换检测线，第 3 个参数和第 4 个参数用于设置线搜索的步长，在以下示例代码中，函数以 1 为步长搜索所有可能半径的线，并以 $π /180$ 为步长搜索所有可能的角度，我们将在下一节中解释最后一个参数的作用。使用以上参数值调用 cv::HoughLines，可以在示例图像上检测到 15 条线：

// 霍夫变换
std::vector<cv::Vec2f> lines;
cv::HoughLines(contours, lines, 1, PI/180, 130);

(3) 为了可视化检测的结果，可以在原始图像上绘制这些线。但是，需要注意的是，该算法是检测图像中的线而不是线段，因为算法没有给出每条线的端点。因此，绘制的直线会穿过整个图像。为此，对于垂直方向的线，我们计算其与图像水平边界(第一行和最后一行)的交点，并在这两个点之间绘制一条线，对于水平方向的线进行类似的处理(使用第一列和最后一列)。使用 cv::line 函数绘制线条，即使点坐标超出图像范围，此函数也能正常工作。因此，无需检查计算出的交点是否落在图像内。最后，通过迭代线向量绘制所有线：

// 绘制检测结果
cv::Mat result(contours.rows, contours.cols, CV_8U, cv::Scalar(255));
image.copyTo(result);
std::cout << "Lines detected: " << lines.size() << std::endl;
std::vector<cv::Vec2f>::const_iterator it = lines.begin();
while (it!=lines.end()) 
    float rho = (*it)[0];
    float theta = (*it)[1];
    if (theta < PI/4. || theta > 3.*PI/4.)     // 竖线
        // 直线与图像第一行交点
        cv::Point pt1(rho/cos(theta), 0);
        // 直线与图像最后一行交点
        cv::Point pt2((rho-result.rows*sin(theta))/cos(theta), result.rows);
        cv::line(result, pt1, pt2, cv::Scalar(255), 1);
     else         // 横线
        // 直线与图像第一列交点
        cv::Point pt1(0, rho/sin(theta));
        // 直线与图像最后一列交点
        cv::Point pt2(result.cols, (rho-result.cols*cos(theta))/sin(theta));
        cv::line(result, pt1, pt2, cv::Scalar(255), 1);
    
    std::cout << "line: (" << rho << "," << theta << ")" << std::endl;
    ++it;

执行以上程序可以得到如下结果：

如上图所示，霍夫变换仅用于寻找图像中边缘像素的对齐方式。偶然的像素对齐，或当多条线通过相同像素对齐时，都可能可能会产生一些错误检测。

2.3 概率霍夫变换

为了克服霍夫变换的问题，并能够检测线段(即具有端点)，已经提出了霍夫变换的改进版本，即概率霍夫变换，在 OpenCV 中使用 cv::HoughLinesP 函数实现。

(1) 使用 cv::HoughLinesP 函数创建封装函数参数的 LineFinder 类：

class LineFinder 
    private:
        // 原始图像
        cv::Mat img;
        // 检测到的线段的端点向量
        std::vector<cv::Vec4i> lines;
        // 累加器参数
        double deltaRho;
        double deltaTheta;
        // 最小得票数
        int minVote;
        // 线段最小长度
        double minLength;
        // 线段最大允许间隙
        double maxGap;
    public:
        // 默认参数
        LineFinder() : deltaRho(1), deltaTheta(PI/180), minVote(10), minLength(0.), maxGap(0.)

(2) 创建对应的 setter 方法：

// 参数设置
void setAccResolution(double dRho, double dTheta) 
    deltaRho = dRho;
    deltaTheta = dTheta;

void setMinVote(int minv) 
    minVote = minv;

void setLineLengthAndGap(double length, double gap) 
    minLength = length;
    maxGap = gap;

(3) 使用上述方法，创建霍夫线段检测方法 findLines：

// 应用概率霍夫转换
std::vector<cv::Vec4i> findLines(cv::Mat& binary) 
    lines.clear();
    cv::HoughLinesP(binary, lines, deltaRho, deltaTheta, minVote, minLength, maxGap);
    return lines;

(4) findLines 方法返回一个 cv::Vec4i 向量，每个向量包含检测到的线段的起点和终点坐标。然后使用方法 drawDetectedLines 在图像上绘制检测到的线条：

// 绘制检测到的线段
void drawDetectedLines(cv::Mat& image, cv::Scalar color=cv::Scalar(255, 255, 255)) 
    std::vector<cv::Vec4i>::const_iterator it2 = lines.begin();
    while (it2!=lines.end()) 
        cv::Point pt1((*it2)[0], (*it2)[1]);
        cv::Point pt2((*it2)[2], (*it2)[3]);
        cv::line(image, pt1, pt2, color);
        ++it2;

(5) 接下来，按以下顺序检测线条：

// 创建 LineFinder 实例
LineFinder ld;
// 设置概率霍夫变换
ld.setLineLengthAndGap(100, 20);
ld.setMinVote(60);
// 直线检测
std::vector<cv::Vec4i> li = ld.findLines(contours);
ld.drawDetectedLines(image);
cv::namedWindow("Lines with HoughP");
cv::imshow("Lines with HoughP", image);

代码执行结果如下所示：

2.4 霍夫变换与概率霍夫变换对比

霍夫变换的目标是在二值图像中找到通过足够数量点的所有线，变换通过考虑输入二值图中的每个单独像素点并识别通过它的所有可能的线来完成。当同一条直线经过多个点时，表示这条直线足够重要，可以考虑保留。
霍夫变换使用二维累加器来计算给定线被识别的次数，累加器的大小由所采用指定 $(ρ, θ)$ 搜索步长定义。为了说明变换过程，我们首先创建一个 180x200 的矩阵(对应 $θ$ 的步长为 $π /180$ ， $ρ$ 的步长为 1）：

// 创建霍夫累加器
cv::Mat acc(200, 180, CV_8U, cv::Scalar(0));

累加器是不同 $(ρ, θ)$ 值的映射，因此，该矩阵的每一项对应于一个特定的线。假设在坐标 (50, 30) 处有一个点，那么可以通过遍历所有可能的 $θ$ 角(步长为 $π /180$ )来识别通过该点的所有线，并且计算相应的(四舍五入的) $ρ$ 值：

// 选择一个点
int x=50, y=30;
// 循环所有角
for (int i=0; i<180; i++) 
    double theta = i*PI/180.;
    double rho = x*std::cos(theta)+y*std::sin(theta);
    int j = static_cast<int>(rho+100.5);
    std::cout << i << ", " << j << std::endl;
    acc.at<uchar>(j, i)++;

计算出的 $(ρ, θ)$ 对相对应的累加器的项递增，项表示通过图像的一个点的所有线，换句话说，每个点都投票给一组可能的候选线。如果我们将累加器显示为图像，可以得到以下结果：

以上曲线表示通过所考虑点的所有线的集合。如果我们用点 (30, 10) 执行相同的操作，可以得到以下累加器：

如上图所示，两条结果曲线在相交于一点：对应于通过这两个点的线的交点。累加器对应的项计数加 2，表示有两点通过这条线。如果对二值映射的所有点重复此过程，那么沿给定线对齐的点将令累加器的公共项持续增加。最后，只需要最终的结果累加器中识别局部最大值，以检测图像中的线(即点对齐)。cv::HoughLines 函数中指定的最后一个参数对应于一条线必须收到的最小投票数才能被视为检测到。例如，我们将这个值降低到 50：

cv::HoughLines(test,lines,1,PI/180,50);

使用以上的代码，将获得更多直线，如下图所示：

概率霍夫变换对基本算法进行了改进。首先，在二值图中以随机顺序选择点扫描图像，而不是逐行进行扫描。每当累加器的项达到指定的最小值时，就会沿相应的线扫描图像，并删除所有通过它的点，即使它们尚未投票。这种扫描还决定了将被接受的段的长度，因此，算法定义了两个附加参数，一个是要接受的线段的最小长度，另一个是允许形成连续段的最大像素间隙，这个额外的步骤增加了算法的复杂性，但由于在扫描过程中减少了点的数量，因此总的算法时间运行时间相差无几。
霍夫变换也可用于检测其他几何实体。事实上，任何可以由参数方程表示的实体都可以由霍夫变换检测。

2.5 霍夫变换检测圆

圆对应的参数方程如下：
$r^2=(x-x_0)^2+(y-y_0)^2$
该方程包括三个参数(圆半径和中心坐标)，这表示我们需要一个三维累加器。然而，霍夫变换通常随着其累加器维数的增加而导致性能下降。实际上，在这种情况下，每个点都会增加累加器的大量项，因此，局部峰值的准确定位变得十分困难。为了克服这个问题，已经提出了多种改进策略，OpenCV 中实现的霍夫圆检测使用两次传递的策略，在第一次传递时，使用二维累加器来查找候选的圆圈位置。由于圆周上点的梯度指向半径方向，因此对于每个点，仅沿梯度方向递增累加器中的项(基于预定义的最小和最大半径值)，一旦检测到可能的圆心(即已收到预定义数量的投票)，就会在第二次传递时构建候选半径的一维直方图，此直方图中的峰值对应于检测到的圆的半径。
实现上述策略的 cv::HoughCircles 函数集成了 Canny 检测和 Hough 变换：

cv::GaussianBlur(image, image, cv::Size(5, 5), 1.5);
std::vector<cv::Vec3f> circles;
cv::HoughCircles(image, circles, cv::HOUGH_GRADIENT,
                2,          // 累加器尺寸 (图像尺寸/2)
                20,         // 两个圆之间的最小距离
                200,        // 高阈值 Canny 
                60,         // 最小投票数
                15, 50);    // 能接受的最大最小圆半径

需要注意的是，在调用 cv::HoughCircles 函数之前平滑图像可以减少导致错误圆检测的图像噪声。检测结果由 cv::Vec3f 实例的向量给出，前两个值是圆心，第三个值是半径；CV_HOUGH_GRADIENT 参数对应于二次圆检测方法；第 4 个参数定义累加器分辨率，它是一个分频因子；例如，指定值 2 则累加器大小为图像大小的一半；第 5 个参数是两个检测到的圆之间的最小像素距离，第 6 个参数对应于 Canny 边缘检测器的高阈值，Canny 检测器的低阈值被设置为该参数值的一半；第 7 个参数是中心位置在第一次传递期间必须获得的最小票数，票数达到时才能被视为第二次传递的候选圆。最后两个参数是要检测的圆的最小和最大半径值。
一旦获得检测到的圆的向量，就可以迭代向量并调用 cv::circle 绘图函数在图像上绘制这些圆：

std::vector<cv::Vec3f>::const_itera以上是关于OpenCV实战（14）——图像线条提取的主要内容，如果未能解决你的问题，请参考以下文章 
 OpenCV与EmguCV中的图像轮廓提取
 OpenCV实战——拟合直线
 OpenCV实战——使用MSER提取特征区域
 OpenCV实战 | 基于形态学运算提取图像中的音符
 OpenCV实战 | 基于形态学运算提取图像中的音符
 OpenCV实战 | 基于形态学运算提取图像中的音符