数据分析 第十篇：分类（kNN）

Posted 2021-01-31 ljhdo

K最近邻(kNN，k-NearestNeighbor)算法是一种监督式的分类方法，但是，它并不存在单独的训练过程，在分类方法中属于惰性学习法，也就是说，当给定一个训练数据集时，惰性学习法简单地存储或稍加处理，并一直等待，直到给定一个检验数据集时，才开始构造模型，以便根据已存储的训练数据集的相似性对检验数据集进行分类。惰性学习法在提供训练数据集时，只做少量的计算，而在进行分类或数值预测时做更多的计算。kNN算法主要用于模式识别，对于随机分布的数据集分类效果较差，对于类内间距小，类间间距大的数据集分类效果好，而且对于边界不规则的数据效果好于线性分类器。常用于推荐系统：推荐受众喜欢电影、美食和娱乐等。

一，kNN算法逻辑

kNN算法的核心思想是：如果一个数据在特征空间中最相邻的k个数据中的大多数属于某一个类别，则该样本也属于这个类别（类似投票），并具有这个类别上样本的特性。通俗地说，对于给定的测试样本和基于某种度量距离的方式，通过最靠近的k个训练样本来预测当前样本的分类结果。

例如，借用百度的一张图来说明kNN算法过程，要预测图中Xu的分类结果，先预设一个距离值，只考虑以Xu为圆心以这个距离值为半径的圆内的已知训练样本，然后根据这些样本的投票结果来预测Xu属于w1类别，投票结果是4：1。

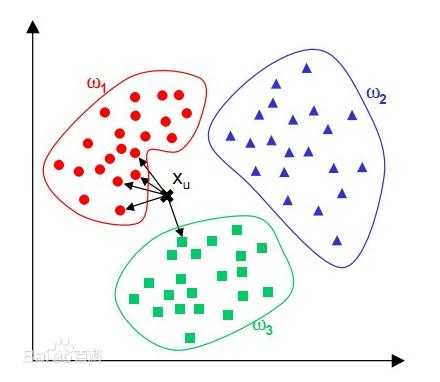
kNN算法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
kNN算法在类别决策时，只与极少量的相邻样本有关。
由于kNN算法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，kNN方法较其他方法更为适合。

1，kNN算法的计算步骤

kNN算法就是根据距离待分类样本A最近的k个样本数据的分类来预测A可能属于的类别，基本的计算步骤如下：

• 对数据进行标准化，通常是进行归一化，避免量纲对计算距离的影响；
• 计算待分类数据与训练集中每一个样本之间的距离；
• 找出与待分类样本距离最近的k个样本；
• 观测这k个样本的分类情况；
• 把出现次数最多的类别作为待分类数据的类别。

计算距离的方法有："euclidean"（欧氏距离）,”minkowski”（明科夫斯基距离）, "maximum"（切比雪夫距离）, "manhattan"（绝对值距离）,"canberra"（兰式距离）, 或 "minkowski"（马氏距离）等。

2，kNN算法如何计算距离？

在计算距离之前，需要对每个数值属性进行规范化，这有助于避免较大初始值域的属性比具有较小初始值域的属性的权重过大。

• 对于数值属性，kNN算法使用距离公式来计算任意两个样本数据之间的距离。
• 对于标称属性（如类别），kNN算法使用比较法，当两个样本数据相等时，距离为0；当两个样本数据不等时，距离是1。
• 对于缺失值，通常取最大的差值，假设每个属性都已经映射到[0,1]区间，对于标称属性，设置差值为1；对于数值属性，如果两个元组都缺失值，那么设置差值为1；如果只有一个值缺失，另一个规范化的值是v，则取差值为 1-v 和 v 的较大者。

3，kNN算法如何确定k的值？

k的最优值，需要通过实验来确定。从k=1开始，使用检验数据集来估计分类器的错误率。重复该过程，每次k增加1，允许增加一个近邻，选取产生最小错误率的k。一般而言，训练数据集越多，k的值越大，使得分类预测可以基于训练数据集的较大比例。在应用中，一般选择较小k并且k是奇数。通常采用交叉验证的方法来选取合适的k值。

R的kknn包中包含两个自动选择最优参数的函数：train.kknn和cv.kknn，前者采用留一交叉验证做参数选择，后者采用交叉验证做参数选择（可以自己选择折数）：

train.kknn(formula, data, kmax = 11, ks = NULL, distance = 2, kernel = "optimal",
    ykernel = NULL, scale = TRUE, contrasts = c(‘unordered‘ = "contr.dummy",
    ordered = "contr.ordinal"), ...)
cv.kknn(formula, data, kcv = 10, ...)

参数注释：

kmax：最大的k值

• ks：向量，用于指定k值，如果非null，那么ks覆盖kmax的值。
• distince：Minkowski距离的参数
• kernel：有效值是："rectangular" (which is standard unweighted knn), "triangular", "epanechnikov" (or beta(2,2)), "biweight" (or beta(3,3)), "triweight" (or beta(4,4)), "cos", "inv", "gaussian" and "optimal".
• kcv：k-fold交叉验证的分区数量

函数的返回值：

best.parameters：列出最佳的k和kernel

fitted.values：内核和k的所有组合的预测列表。

MISCLASS：分类错误的矩阵，用于查看错误率

二，kNN算法的R实现

R语言实现kNN算法的函数包主要有：

• class函数包中的knn、knn.cv函数；
• caret函数包中的knn3函数；
• kknn函数包中的kknn函数；

class包是比较基础的，kknn是优化之后的算法。
例如，使用kknn包执行kNN算法，对检验数据集进行分类：

mydata <- read.csv(file=‘C:/BlackFriday.csv‘,header=TRUE,stringsAsFactors = TRUE)
dt <- mydata[,c(‘Gender‘,‘Age‘, ‘Occupation‘,‘City_Category‘,‘Stay_In_Current_City_Years‘, ‘Marital_Status‘,‘Product_Category‘)]

dt$Occupation <- factor(as.character(dt$Occupation))
dt$Product_Category=factor(as.character(dt$Product_Category))

mydt <- dt[1:10000,]

library(kknn)

m <- dim(mydt)[1]
val <- sample(1:m,round(m/10),replace = TRUE)

dt.learn <- mydt[-val,]
dt.test <- mydt[val,]

myk <- train.kknn(Product_Category~.,dt.learn)
k <- myk$best.parameters # get best parameters of kNN

myknn <- kknn(Product_Category ~.,dt.learn,dt.test,k=11)

summary(myknn)

fit <- fitted(myknn)
table(fit,dt.test$Product_Category)

 

 

 

 

 

参考文档：

KNN算法的R语言实现