容斥原理

Posted 2021-01-31 zcy0917

图片版（你可以选择先不看）

https://www.sohu.com/a/204271684_614593（对，我就是那个黄色的链接）

---

 

在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

ta的公式是这样滴：

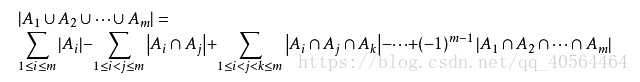
下面我们开始正式讲解一下

设S为有限集,  ,则 两个集合的容斥关系公式：A∪B =|A∪B| = |A|+|B| - |A∩B |(∩：重合的部分）

三个集合的容斥关系公式：|A∪B∪C| = |A|+|B|+|C| - |A∩B| - |B∩C| - |C∩A| + |A∩B∩C|（如果你看完下面的之后还是不懂，咳咳，那你就仔细看看上面的那个黄色的链接，那个是图片版）

详细推理如下（文字版）：

1、 等式右边改造   = { [（A+B - A∩B）+C - B∩C] - C∩A }+ A∩B∩C

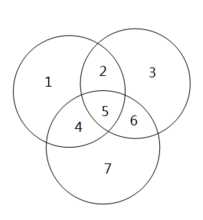
2、文氏图分块标记，如右图：1245构成A，2356构成B，4567构成C

3、等式右边（）里指的是下图的1+2+3+4+5+6六部分： 那么A∪B∪C还缺部分7。

4、等式右边[]号里+C（4+5+6+7）后，相当于A∪B∪C多加了4+5+6三部分， 减去B∩C（即5+6两部分）后，还多加了部分4。

5、等式右边{}里减去C∩A （即4+5两部分）后，A∪B∪C又多减了部分5， 则加上A∩B∩C（即5）刚好是A∪B∪C。

 对于上面的公式，简单理解呢就是，对于它们相交的部分，如果是奇数个相交就加起来，偶数个就减去   (奇加偶减）

其实我认为容斥原理就是 一个帮助你解题的数学思想。

一些可以帮助你理解的例题：

https://blog.csdn.net/TRiddle/article/details/51873991