dp单调性优化

Posted 2021-01-31 chdy

　　跟着书上的思路学习dp的单调性优化觉得还是很容易想的。

数据范围：

dp，数据范围是百万，这应该是O(n)的算法了。

首先不难想到设f[i]表示到第i个百米所能达到的最大能量，那么f[n]即为所求。

f[i]=max(f[i],f[j]+s[i]-s[j]-cost[i]);这个地方s数组是能量的前缀和，然后发现需要多加一层循环来枚举j，这个时候就是O(n^2)的算法了。

这样的话，就只有40分了，毕竟看分做题。这分给的还是很良心的。

考虑优化首先我们发现状态转移方程可以这样变f[i]=max{f[j]-s[j]}+s[i]-cost[i];我们这需要找到一个最大的f[j]-s[j]的即可

且f[j]还必须>=cost[i];因为这是判断能否调到也就是一个状态合法与否。

这样我们就可以维护一个双端队列来维护了！队首永远最优至于合法否我们需要小小的判断一下。

#include<bits/stdc++.h>
#include<iomanip>
#include<iostream>
#include<ctime>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdio>
#include<vector>
#include<queue>
#include<deque>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<cstdlib>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    if(x==0){putchar(‘0‘);putchar(‘
‘);return;}
    if(x<0){putchar(‘-‘);x=-x;}
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+‘0‘,x/=10;
    while(num)putchar(ch[num--]);
    putchar(‘
‘);return;
}
const int MAXN=2000002;
int v[MAXN],cost[MAXN];
int f[MAXN];//f[i]表示前i百米所能得到的最大能量
int q[MAXN],h=1,t=1;
int n,m;
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();f[0]=m;
    for(int i=1;i<=n;i++)
    {
        v[i]=read();
        cost[i]=i*100;
        v[i]+=v[i-1];
    }
    q[h]=0;
    for(int i=1;i<=n;i++)
    {
        while(f[q[h]]<cost[i])h++;//题目中给出保证一定能吃完，所以这个地方不需要加h<t
        f[i]=f[q[h]]-cost[i]-v[q[h]]+v[i];
        while(f[q[t]]-v[q[t]]<f[i]-v[i])t--;
        q[++t]=i;
    }
    put(f[n]);
    return 0;
}

显然成功了呢，复杂度就是O(n)因为每个点进出队伍一次。

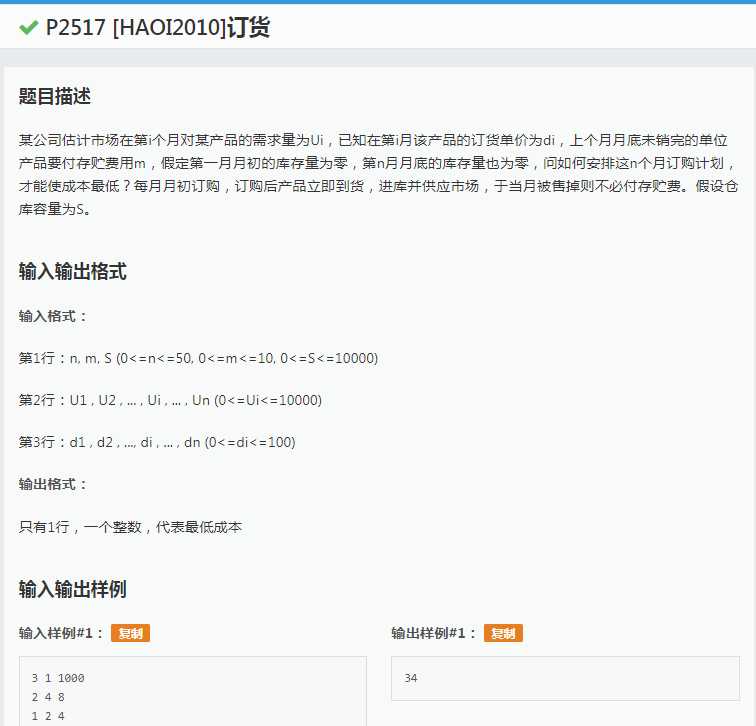
对于这个题目，我竟然直接手残翻开了书，看到了状态转移方程式。哎，自己没想。

其实状态转移方程也很好想，状态设为：f[i][j]表示第i个月存仓j个零件所得到的最低成本。

由此可得，f[i][j]=min{f[i-1][k]+(u[i]+j-k)*d[i]+m*k}其中j<=s,k<=j+u[i].(显然你不能把上个月的零件卖了)

由于k这个决策也需要枚举所以复杂度是O(n*s*s)的，s那么大这肯定炸啊。预期得分也是40。

搞一下优化，大括号里得到貌似都和k有关不如先展开再说。

f[i][j]=min{f[i][k]+(m-d[i])*k}+(u[i]+j)*d[i];这样的话只有f[i][k]和(m-d[i])*k和当前决策有关了，考虑维护一个最优决策那不就可以直接进行转移了么

这样的话就是O(n*s)的啊，能A。所以考虑维护一个单调队列，等等为什么要维护队列，队列中的其他值有用么，发现只要k属于它应该属于的范围之内的话，那么这个决策就一定是合法的，所以为什么要队列，直接一个值保存即可，这样每次和生成出来的值比较哪个更小不就有了最优解么。

这里就大功告成了,乌拉。

#include<bits/stdc++.h>
#include<iomanip>
#include<iostream>
#include<cstdio>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<queue>
#include<deque>
#include<map>
#include<set>
#include<bitset>
#include<stack>
#include<vector>
#include<cstdlib>
#include<algorithm>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
    return x*f;
}
inline void put(int x)
{
    if(x==0){putchar(‘0‘);putchar(‘
‘);return;}
    if(x<0)x=-x,putchar(‘-‘);
    int num=0;char ch[50];
    while(x)ch[++num]=x%10+‘0‘,x/=10;
    while(num)putchar(ch[num--]);
}
const int MAXN=100;
int n,m,s,p=0;
int u[MAXN],d[MAXN];
int f[2][10002];//f[i][j]表示第i个月保存j个商品所需最小费用。
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();s=read();
    for(int i=1;i<=n;i++)u[i]=read();
    for(int i=1;i<=n;i++)d[i]=read();
    memset(f,10,sizeof(f));
    f[p][0]=0;
    for(int i=1;i<=n;i++)
    {
        p=p^1;
        int k=0,ans=2147483646;
        for(int j=0;j<=s;j++)//枚举保存多少个商品
        {
            for(;k<=min(j+u[i],s);k++)//提供状态转移
            //为什么最优的状态一定是ans呢？
            //考虑到需要一个k值使ans最小且合法，合法那一定是<=min(j+u[i],s)
            //得到ans就是最优的了，很显然吧，复杂度为n*s
                ans=min(ans,f[p^1][k]+(m-d[i])*k);
            f[p][j]=ans+(u[i]+j)*d[i];
        }
    }
    put(f[p][0]);
    return 0;
}

显然的，我们发现当前状态只和上一个状态有关所以可以开滚动数组优化空间啊。这点完美意识还是需要的。

那么经过这两道题，相信单调性优化都了解的差不多了。可以深入学习一些其他优化了呢。