各项概念解释和用途
Posted muffe
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了各项概念解释和用途相关的知识,希望对你有一定的参考价值。
1、方差是各个数据分别与其平均数之差的平方的和的平均数,用字母D表示。在概率论和数理统计中,方差(Variance)用来度量随机变量和其数学期望(即均值)之间的偏离程度。在许多实际问题中,研究变量和均值之间的偏离程度有着重要意义。
其中,x表示样本的平均数,n表示样本的数量,xi表示个体,而s^2就表示方差。用途:方差和期望的距离越大就越极端。
2、平方差公式(difference of two squares)是数学公式的一种,它属于乘法公式、因式分解及恒等式,被普遍使用。平方差指一个平方数或正方形,减去另一个平方数或正方形得来的乘法公式:a2-b2=(a+b)(a-b)
3、标准差(Standard Deviation) ,又常称均方差,但不同于均方误差(mean squared error,均方误差是各数据偏离真实值的距离平方的平均数,也即误差平方和的平均数,计算公式形式上接近方差,它的开方叫均方根误差,均方根误差才和标准差形式上接近),标准差是离均差平方和平均后的方根,用σ表示。假设有一组数值X1,X2,X3,......XN(皆为实数),其平均值(算术平均值)为μ,公式如图
4、均方误差(mean squared error,均方误差是各数据偏离真实值的距离平方的平均数,也即误差平方和的平均数,计算公式形式上接近方差,它的开方叫均方根误差,(加上根就是2)均方根误差才和标准差形式上接近):

均方根误差:是均方误差的算术平方根。
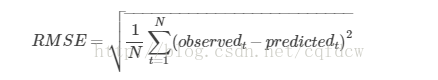
以上是关于各项概念解释和用途的主要内容,如果未能解决你的问题,请参考以下文章

