「Luogu P2508」[HAOI2008]圆上的整点 解题报告

Posted 2021-01-30 hovny

题面

给定圆的半径，求圆上整点数

这是一道很Nice的数学题！超爱！好吧，由于这道题，我去Study了一下复数(complex number)复杂的数

真棒！！！

有兴趣的戳这里！！！(huge o)

思路：

高斯素数的原理，将整数分解质因数后，再把每个质因数分解成高斯素数，对于质数4n+1，它可以有效的分解成高斯素数，而质数4n+3不能，因为3无法分解为高斯素数，所以当一个数有奇数个3因子时，这个圆上没有整点，而3的个数为偶数时，由于能分成两组配对，所以有整点，但3对Ans的影响为0，因为x*1=x，因此只要不变就行了，当由于2的高斯素数表示为1-i*1+i，所以2的个数对Ans无影响

对于25如下：

[ large 25=5 imes 5 ]

[ large 25=(2-i)(2+i)(2-i)(2+i) ]

所以：

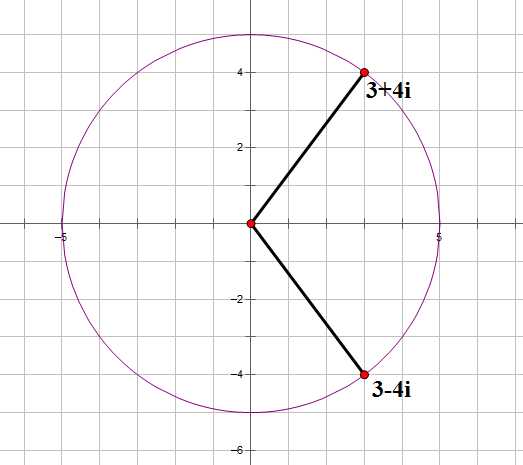
Left	Right
(large 1)	(large 1)
(large 2-i)	(large 2+i)
(large 2-i)	(large 2+i)
(large =3-4i)	(large =3+4i)

这是一种情况(large (3,-4))

Left	Right
(large 2-i)	(large 2-i)
(large 2+i)	(large 2+i)
(large =5)	(large =5)

这是一种情况(large (5,0))

Left	Right
(large 2+i)	(large 2+i)
(large 2+i)	(large 2+i)
(large =3+4i)	(large =3-4i)

这是一种情况(large (3,-4))

而对于上述

(large imes)	(large 3-4i)	(large 5)	(large 3+4i)
(large -1)	(large -1+4i)	(-5)	(large -3-4i)
(large i)	(large 4+3i)	(large 5i)	(large -4+3i)
(large -i)	(large -4-3i)	(large -5i)	(large 4-3i)

所以一共有点对12对

那么高斯素数怎么表示点呢？

它只要一个数，就可以表示点的坐标，RT：

Code：

#include<bits/stdc++.h>
#define N 10000010
#define ll long long
using namespace std;
ll n,m,res,ans=4;
ll a[N],t,T;
ll p[N];
ll s[N];
bool b[N];
int main()
{
    ll i,j;
    scanf("%lld",&n);
    m=n;
    for(i=2;i*i<=m;i++)
    {
        if(!b[i])
        {
            a[++T]=i;
            if(m%i==0)
            {
                p[++t]=i;
                while(m%i==0)
                {
                    m/=i;
                    s[t]++;
                }
            }
        }
        for(j=1;j<=T;j++)
        {
            if(a[j]*i*i*a[j]>m)
                continue;
            b[a[j]*i]=1;
            if(i%a[j]==0)
                continue;
        }
    }
    if(m>1)
    {
        p[++t]=m;
        s[t]=1;
    }
    for(i=1;i<=t;i++)
        if((p[i]-1)%4==0)
            ans*=(2*s[i]+1);
    printf("%lld",ans);
    return 0;
}