0-1背包问题的动态规划法与回溯法

Posted 2021-01-30 clwsec

一、动态规划

状态转移方程：

 1 从前往后：
 2 if(j>=w[i])
 3     m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
 4 else
 5     m[i][j]=m[i-1][j];
 6  
 7 从后往前：
 8 if(j>=w[i])
 9     m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
10 else
11     m[i][j]=m[i+1][j];

算法：

 1 从前往后：
 2 for(int i=1;i<=n;i++)
 3     for(int j=1;j<=c;j++)
 4     {
 5         if(j>=w[i])
 6         {
 7             m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
 8         }
 9         else//这里没有考虑j<0的情况，因为算法中j取不到
10         {
11             m[i][j]=m[i-1][j];
12         }
13     }
14  
15 从后往前：
16 for(int i=n;i>=1;i--)
17     for(int j=1;j<=c;j++)
18     {
19         if(j>=w[i])
20         {
21             m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
22         }
23         else
24         {
25             m[i][j]=m[i+1][j];
26         }
27     }

例子：

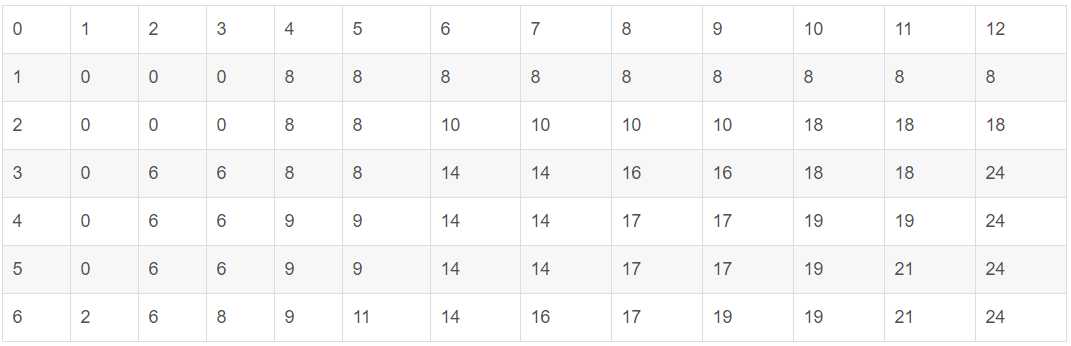
例：0-1背包问题。在使用动态规划算法求解0-1背包问题时，使用二维数组m[i][j]存储背包剩余容量为j，可选物品为i、i+1、……、n时0-1背包问题的最优值。绘制

重量数组w = {4, 6, 2, 2, 5, 1}，

价值数组v = {8, 10, 6, 3, 7, 2}，

背包容量C = 12时对应的m[i][j]数组。（从前往后）

例题代码 :

 1 #include<iostream>
 2 #include<cmath>
 3 #include<cstring>
 4 #define N 20
 5 using namespace std;
 6 int main()
 7 {
 8     int w[N]={0,4,6,2,2,5,1},v[N]={0,8,10,6,3,7,2};
 9     int m[N][N];
10     memset(m,0,sizeof(m));
11     int n=6,c=12;   //n,c均要小于N 
12     for(int i=1;i<=n;i++)
13     for(int j=1;j<=c;j++)
14     {
15         if(j>=w[i])
16         {
17             m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
18         }
19         else
20         {
21             m[i][j]=m[i-1][j];
22         }
23     }
24     cout<<m[n][c]<<endl; //从前往后
25  
26     /*
27     for(int i=n;i>=1;i--)
28     for(int j=1;j<=c;j++)
29     {
30         if(j>=w[i])
31         {
32             m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
33         }
34         else
35         {
36             m[i][j]=m[i+1][j];
37         }
38     }
39     cout<<m[1][c]<<endl;//从后往前
40     */
41     return 0;
42 }

二、回溯法

 1进入左子树条件：cw+w[i]<=c   //cw为当前重量

 2进入右子树条件（减枝函数）：cp+r>bestp   //cp为当前价值，bestp为当前最优价值，r为当前剩余物品价值总和。cp+r由函数     Bound计算。

 3需要先将物品按单位重量价值从大到小排序，按序进入左子树；进入右子树时，由函数Bound计算当前节点上界，只有其上界大于当前最优价值bestp时，才进入右子树，否则减去。

算法：

 1 void Backtrack(int i)
 2 {
 3     if(i>n)  //到达叶节点
 4     {
 5         bestp=cp; 
 6         return;
 7     }
 8     if(cw+w[i]<=c)  //进入左子树
 9     {
10         cw+=w[i];
11         cp+=v[i];
12         Backtrack(i+1);
13         cw-=w[i];
14         cp-=v[i];
15     }
16     if(Bound(i+1)>bestp)  //进入右子树
17     {
18         Backtrack(i+1);
19     }
20 } 
21  
22 int Bound(int i)  //计算上界
23 {
24     int cleft=c-cw;
25     int b=cp;          
26     while(i<=n&&w[i]<=cleft)  //以物品单位重量价值递减序装入物品
27     {
28         cleft-=w[i];
29         b+=v[i];
30         i++;
31     }
32     if(i<=n)//装满背包
33     {
34         b+=v[i]*(cleft/w[i]);
35     }
36     return b;
37 }

例子代码：

 1 #include<iostream>
 2 #define N 20
 3 using namespace std;
 4 int w[N]={0,4,6,2,2,5,1},v[N]={0,8,10,6,3,7,2};
 5 int n=6,c=12;
 6 int cp=0,cw=0,bestp=0;
 7 int Bound(int i)  //计算上界
 8 {
 9     int cleft=c-cw;
10     int b=cp;          
11     while(i<=n&&w[i]<=cleft)  //以物品单位重量价值递减序装入物品
12     {
13         cleft-=w[i];
14         b+=v[i];
15         i++;
16     }
17     if(i<=n)//装满背包
18     {
19         b+=v[i]*(cleft/w[i]);
20     }
21     return b;
22 }
23 void Backtrack(int i)
24 {
25     if(i>n)  //到达叶节点 
26     {
27         bestp=cp; 
28         return;
29     }
30     if(cw+w[i]<=c)  //进入左子树
31     {
32         cw+=w[i];
33         cp+=v[i];
34         Backtrack(i+1);
35         cw-=w[i];
36         cp-=v[i];
37     }
38     if(Bound(i+1)>bestp)  //进入右子树 
39     {
40         Backtrack(i+1);
41     }
42 } 
43  
44 int main()
45 {
46     Backtrack(1);
47     cout<<bestp<<endl;
48     return 0;
49 }