字典树

Posted 2021-01-30 noncontradiction

字典树，通常解决大量拥有相同前缀的字符串问题，有时候也是二进制数问题（字典树起初是链表写，但是比较麻烦，感觉数组更好一些，链表无非就是next换成*next，空间用的时候定义）

 

第一次听学长讲字典树的时候讨论这么一个问题，就是网址假如有1e10个，但是每个网址前面都有http，所以要是每个都直接存，光http就要花费4*1e10空间，但是如果要是用字典树压缩一下，就变成了4了

 

字典树如果要存储的字符串有26种，其实就是26叉树，m种，就是m叉树

开始树是空的，每个节点其实都代表一个字符，并且每个节点往下最多有m个节点

每个节点都是一个结构体，每个点类似链表一样（链表只能指向下一个，而这个能指向m个），该点可能还要记录 是不是某个（或者是多少个）字符串的尾

Struct s

{
int v;

    Int next[26];

}f[1005];

v通常根据情况而定，有时候可以记录当前为结尾的字符串有多少，也可以是含有当前的前缀的字符串有多少

通常next没有值的时候可以赋值成0，因为这是一棵树，所以他要是往0（根）跳是不可能的。

Int tot；

tot通常用于记录结构体数组已经使用多少了，所以当需要定义新的的时候，放入到f[tot]即可

对于只包含26个字符的字典树，通常开一个next[26]的数组(如果对于二进制数字只包含01串的话，next[2]即可)

假如输入字符串AC和AA以后

 

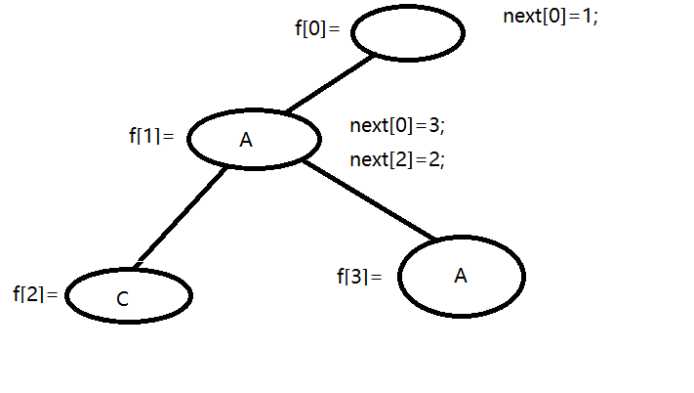
Hdu1251，开始给定一堆字符串，让你找某个字符串是多少个给定字符串的前缀

#include<stdio.h>
#include<string.h>
int len;
struct s
{
    int v;
    int next[27];
}f[1000005];
char str[105];
int tot;
void mem(int x)
{
    f[x].v=0;
    for(int i=0;i<26;i++)
        f[x].next[i]=0;
}
void add()
{
    int z=0,zz;///z从根开始，一直记录到达的节点
    for(int i=0;i<len;i++)
    {
        zz=str[i]-‘a‘;
        if(!f[z].next[zz])///如果之前没有这条路的话，就建立一个
        {
            mem(tot);///清空结构体
            f[z].next[zz]=tot++;
        }
        z=f[z].next[zz];
        f[z].v++;///因为一会要记录前缀有多少个，所以每个字符串都把自己的前缀+1即可
    }
}
int query()
{
    int z=0,zz;
    for(int i=0;i<len;i++)
    {
        zz=str[i]-‘a‘;
        if(!f[z].next[zz])///说明没有以他为前缀的
            return 0;
        z=f[z].next[zz];
    }
    return f[z].v;
}
int main()
{
    mem(0);
    tot=1;
    int zt=0;
    while(gets(str))
    {
        len=strlen(str);
        if(len==0)
        {
            zt=1;
         continue;
        }
        if(zt)
        printf("%d
",query());
        else
          add();
    }
}