多元正态分布
Posted hikigaya-hachiman
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了多元正态分布相关的知识,希望对你有一定的参考价值。
随即变量概率分布
我们将p个随机变量X1,X2,X3...Xp整体称为p维随机向量,记为X=(X1,X2,X3....Xp)‘ 。
我们可以将X理解为一个p维欧式空间中的一个向量。
其概率分布参照一维随机变量即可
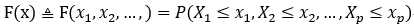
离散型随机变量:
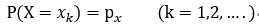
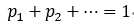
连续型随机变量:
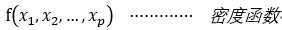
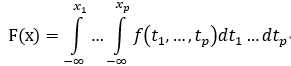
考点:
1.证明某函数是密度函数
首先密度函数在定义域内处处不为负,其次密度函数从负无穷到正无穷的积分值为0。
2.求某分量的边缘密度函数,即是对除去该分量以外的所有分量进行积分。
3.询问多个随机变量是否相互独立,对每个分量求解其边缘密度函数,若这些边缘分量函数的乘积等于联合分布密度函数,则说明它们相互独立。
随机向量的数字特征
离散型随机变量:
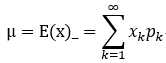
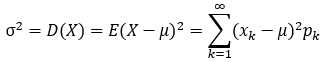
连续型随机变量:
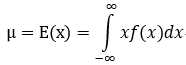
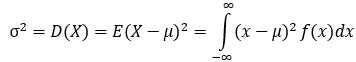
D(X)有一个简单的计算公式:
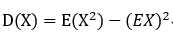
以上是关于多元正态分布的主要内容,如果未能解决你的问题,请参考以下文章