图图的存储图的遍历

Posted 2021-01-29 siyyawu

图（Graph）是由顶点的有穷非空集合和顶点之间的边组成。G（V,E） V表示顶点的集合，E表示边的集合。

在无向图中，边可以表示为E1={(A,D),(B,C)}

在有向图中，顶点v1和v2的有向边称为弧。表示为<v1,v2> v1称为弧尾，v2称为弧顶。

在无向图中，如果任意边两个顶点都存在边，则该图为无向完全图，n个顶点的无向完全图有n*(n-1)/2条边。

在有向图中，如果任意边两个顶点都存在互为相反边，则该图为有向完全图，n个顶点的有向完全图有n*(n-1)条边。

稀疏图，稠密图。

带权图称为网。

子图如下。

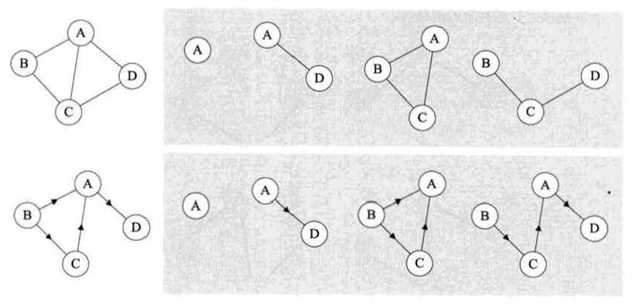
无向图的度指的是顶点关联的边的数量，容易得出总边数=度的总数/2

有向图分为出度和入度，以顶点为弧尾的边的数量为出度，以顶点为弧顶的边的数量称为入度。

第一个顶点到最后一个顶点相同的路径称为回路或环 (Cycle）。 序列中顶点不重 复出现的路径称为简单路径. 除了第一个顶点和最后一个顶点之外，其余顶点不重复 出现的回路，称为简单回路或简单环。

 

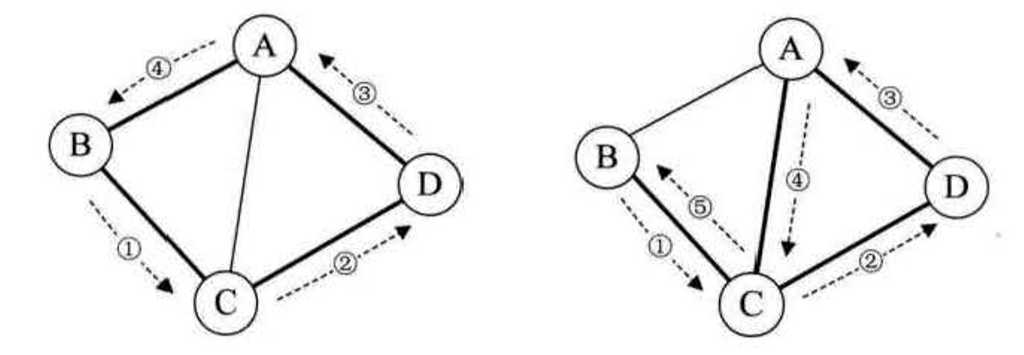
任意顶点都是连通的称为连通图。

无向图中的极大连通子图称为连通分量。

有向图中，所有顶点都存在路径称为强连通图，左图不是强连通图，右图是强连通图，同时右图是左图的极大强连通子图。

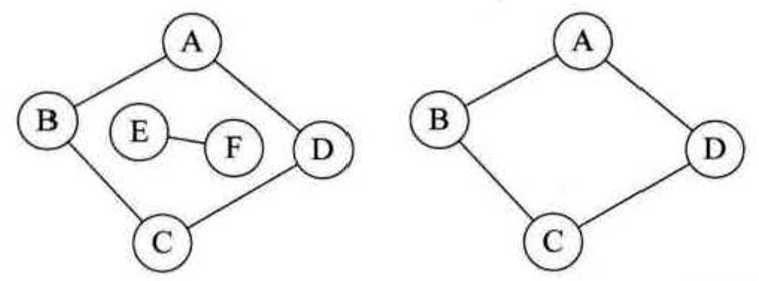
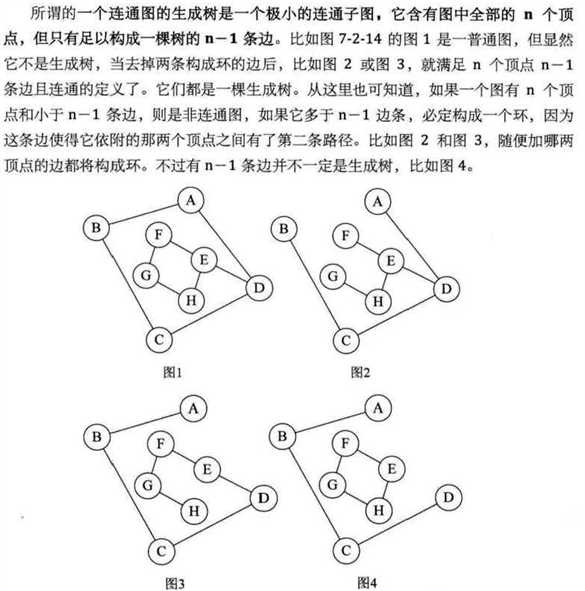
连通图的生成树是极小的的连通子图

 

---

---

 

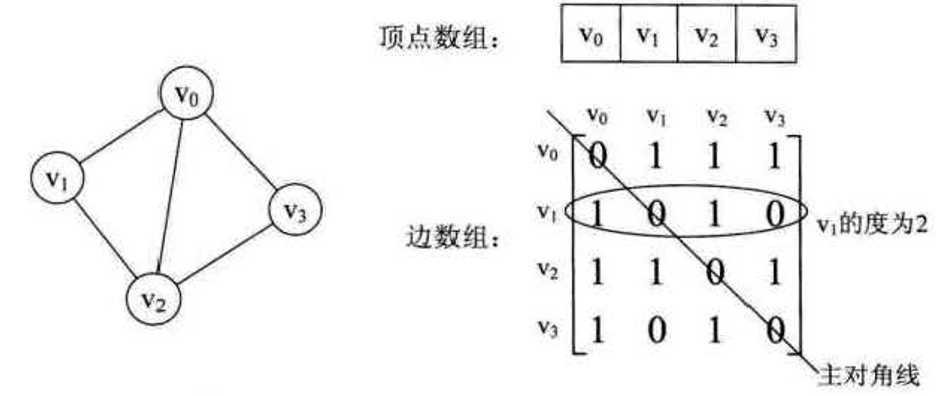
图通常有五种存储方式，邻接矩阵、邻接表、十字链表、邻接多重表、边集数组。

 邻接矩阵用一个一维数组来表示顶点，用一个二维数组来表示边。

对于无向图来说，矩阵是一个对称矩阵。

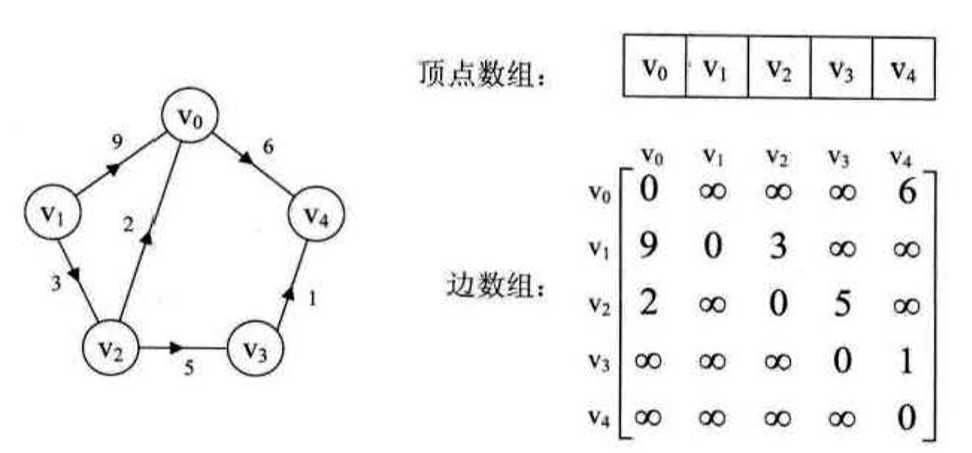
对于有向图，可以把边表中没有弧的地方设为-1。

---

 

邻接表是对邻接矩阵的改进，由于稀疏图中边很少，所有二维数组中很多地方都为0。我们可以用链表存储顶点信息，同时保存一个指向边表的结点。

同一个顶点指向的单链表不分先后顺序。

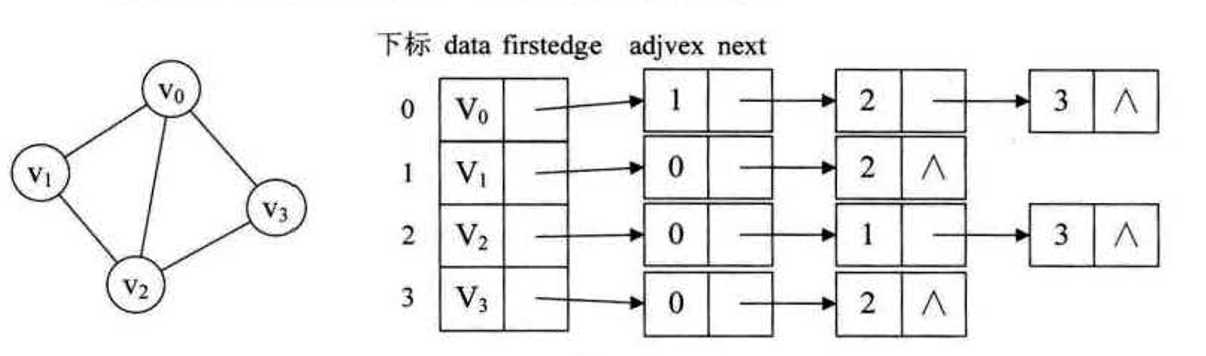
有向图 的邻接表（结点不分先后）

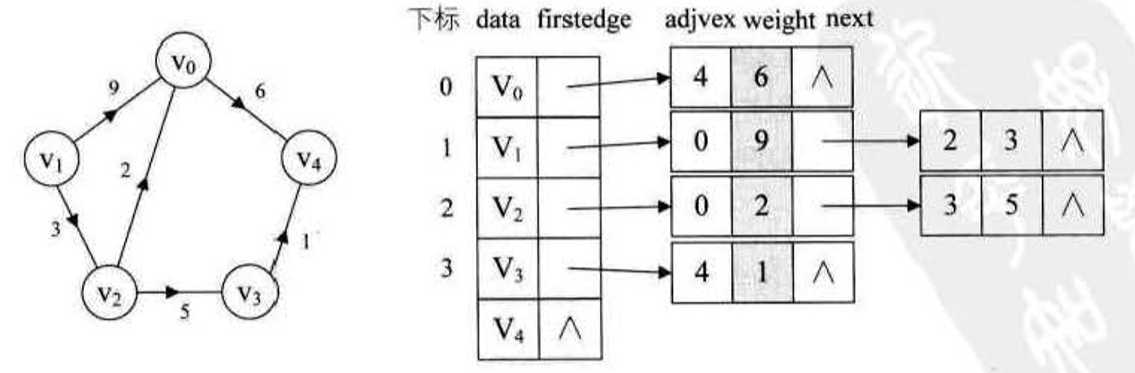
带权有向图邻接表的实现：

package GraphAdjList;

import java.util.ArrayList;
import java.util.List;

//带权有向图邻接表实现(出度表)
public class GraphAdjList<T>{

    public List<VertexNode<T>> list;
    
    public GraphAdjList(T[] datas)
    {
        list=new ArrayList<VertexNode<T>>();
        System.out.println("初始化顶点表");
        for(int i=0;i<datas.length;i++)
        {
            VertexNode<T> node=new VertexNode<T>();
            node.data=datas[i];
            list.add(node);
        }
    }
    
    
    //增加顶点
    public void insertVertexNode(T x)
    {
        VertexNode<T> node=new VertexNode();
        node.data=x;
        System.out.println("新增顶点");
        list.add(node);
    }
    
    //遍历顶点表
    public void traversalByVertexNode()
    {
        for(VertexNode<T> v:list)
        {
            System.out.println(v.data);
        }
    }
    
    //获取坐标index的顶点
    public VertexNode<T> getVertexNode(int index)
    {
        return list.get(index);
    }
    /**
     * 新增弧
     * @param x 弧头坐标
     * @param ajavex 弧尾坐标
     * @param weight 权值
     */
    public void addEdge(int x,int ajavex,int weight)
    {
        EdgeNode temp=getVertexNode(x).next;
        while(temp!=null)
        {
            temp=temp.next;
        }
        EdgeNode node=new EdgeNode();
        node.ajavex=ajavex;
        node.weight=weight;
        temp.next=node;
    }
}
//顶点表
class VertexNode<T>
{
    T data;
    EdgeNode next;//指向邻接结点的头指针
}

//边表
class EdgeNode
{
    int ajavex;//邻接点坐标
    int weight;//权值
    EdgeNode next;//邻接点指针
}

测试：

package GraphAdjList;

import java.util.List;

public class App {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        String[] str={"V1","V2","V3","V4"};
        GraphAdjList<String> g=new GraphAdjList<String>(str);
        g.traversalByVertexNode();
        g.insertVertexNode("V5");
        g.traversalByVertexNode();
    }

}

结果：

初始化顶点表
V1
V2
V3
V4
新增顶点
V1
V2
V3
V4
V5

---

---

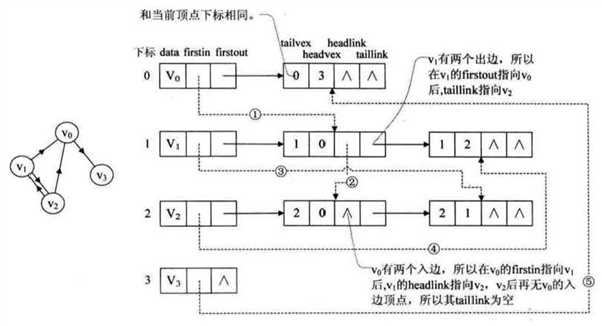
十字链表将出度表和入度表结合起来。

顶点表

边表：

---

---

 

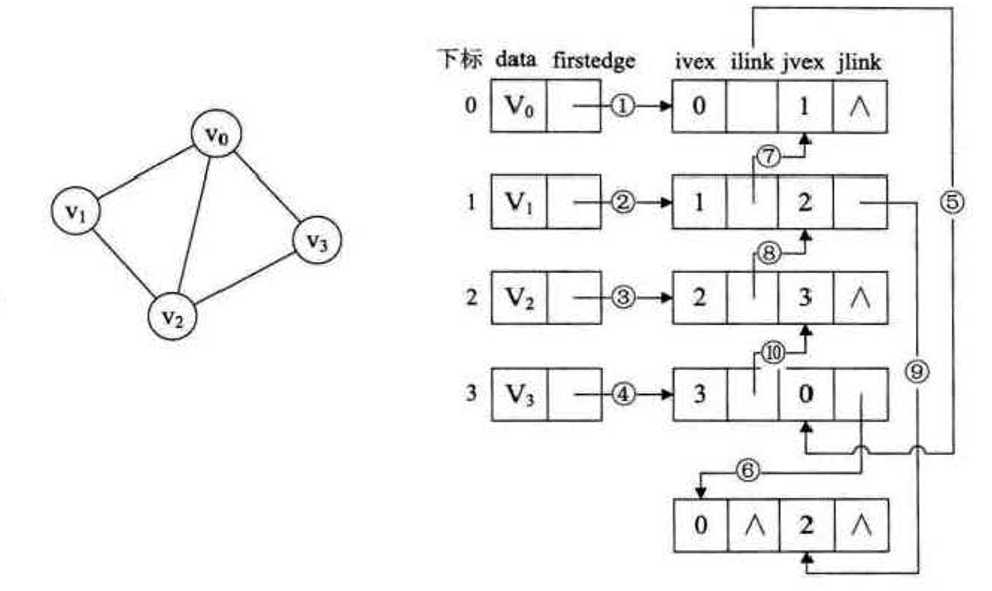
多重邻接表：无向图的优化

---

---

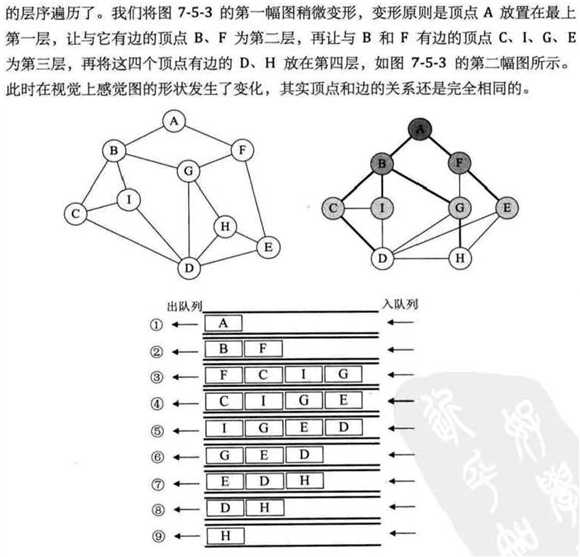
深度遍历和广度遍历：

深度遍历类似树的先序遍历，始终选取靠左/靠右的顶点，如果某个结点连接的结点都被访问后则原路返回。用递归来实现

广度遍历则类似树的层序遍历，将每次出队的顶点的相互连接的顶点入队，用队列来来实现

带权无向图邻接矩阵实现,深度遍历、广度遍历：

 

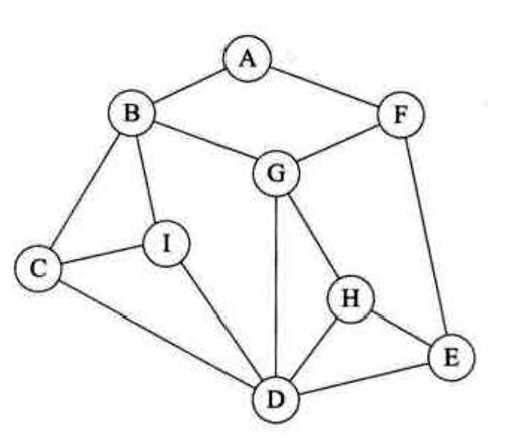
package AMWGraph;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

//带权无向图邻接矩阵实现,深度遍历、广度遍历
public class AMWGraph {

    public List<Object> vertexList;//结点链表
    public int[][] edges;//邻接矩阵
    public int numOfEdges;//边的数目
    public boolean[] isVisited;
    public int count=0;
    public AMWGraph(int n,String[] v)
    {
        isVisited=new boolean[n];
        vertexList=new ArrayList<>();
        edges=new int[n][n];
        for(int i=0;i<n;i++)
        {
            vertexList.add(v[i]);
            isVisited[i]=false;
        }
        numOfEdges=0;
    }
    
    //得到结点数目
    public int getNumOfVertex()
    {
        return vertexList.size();
    }
    
    //得到边的数目
    public int getNumOfEdges()
    {
        return numOfEdges;
    }
    
    
    //得到结点i的数据
    public Object getValueByIndex(int i)
    {
        return vertexList.get(i);
    }
    
    //返回v1,v2的权值
    public int getWeight(int v1,int v2)
    {
        return edges[v1][v2];
    }
    
    //插入结点
    public void insertVertex(Object vertex)
    {
        vertexList.add(vertex);
        System.out.println("增加结点");
        int[][] temp=edges;
        int lengside;
        lengside=getNumOfVertex(); //顶点数量
        edges=new int[lengside][lengside];
        for(int i=0;i<temp.length;i++){
            for(int j=0;j<temp[i].length;j++)
            {
                edges[i][j]=temp[i][j];
            }
        }
        boolean[] isVisitedTemp=isVisited;
        isVisited=new boolean[lengside];
        for(int i=0;i<isVisitedTemp.length;i++)
        {
            isVisited[i]=isVisitedTemp[i];
        }
        isVisited[lengside-1]=false;
     }
    
    //插入边
    public void insertEdge(int v1,int v2,int weight)
    {
        edges[v1][v2]=weight;
        edges[v2][v1]=weight;
        numOfEdges++;
    }
    
    //删除边
    public void deleteEdge(int v1,int v2)
    {
        edges[v1][v2]=0;
        numOfEdges--;
    }
    
    
    //根据一个顶点的下标，返回该顶点的第一个邻接结点的下标
    public int getFirstNeighbor(int index)
    {
        for(int j=0;j<vertexList.size();j++)
        {
            if(edges[index][j]>0)
            {
                return j;
            }
        }
        return -1;
    }
    
    //根据一个邻接结点的下标来取得下一个邻接结点的下标
    public int getNextNeighbor(int v1,int v2)
    {
        for(int j=v2+1;j<vertexList.size();j++)
        {
            if(edges[v1][j]>0)
            {
                return j;
            }
        }
        return -1;
    }
    
    //深度遍历
    public void depthFirstSearch(boolean[] isVisited,int i)
    {
        System.out.println(getValueByIndex(i));
        isVisited[i]=true;
        int w=getFirstNeighbor(i);
        while(w!=-1)
        {
            if(!isVisited[w])
            {
                depthFirstSearch(isVisited,w);
            }
            w=getNextNeighbor(i, w);
        }
    }
    
    //深度优先遍历
    public void depthFirstSearch()
    {
        for(int i=0;i<getNumOfVertex();i++)   //非连通图需要选择多个结点，本结构为连通图
        {
            if(!isVisited[i])
            {
                count++;
                depthFirstSearch(isVisited,i);
            }
        }
    }
    
    //广度优先遍历
    private void broadFirstSearch(boolean[] isVisited,int i)
    {
        int u,w;
        LinkedList<Integer>queue=new LinkedList();
        System.out.println(getValueByIndex(i)+" ");
        isVisited[i]=true;
        
        queue.addLast(i);//坐标进队列
        while(!queue.isEmpty())
        {
            
            u=((Integer)queue.removeFirst());
            w=getFirstNeighbor(i);
            while(w!=-1)
            {
                if(!isVisited[w])
                {
                    System.out.println(getValueByIndex(w)+" ");
                    isVisited[w]=true;
                    queue.addLast(w);
                }
                
                    w=getNextNeighbor(i, w);
            }
        }
    }
    
    //广度遍历
    public void broadFirstSearch()
    {
        for(int i=0;i<getNumOfVertex();i++)
        {
            if(!isVisited[i])
            {
                count++;
                broadFirstSearch(isVisited,i);
            }
        }
    }
    
}

测试：

package AMWGraph;

public class App {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        String[] labels={"A","B","C","D","E","F","G","H","I"};
        AMWGraph graph=new AMWGraph(labels.length,labels);
        graph.insertEdge(0, 1, 1);
        graph.insertEdge(0, 5, 1);
        graph.insertEdge(1, 2, 1);
        graph.insertEdge(1, 8, 1);
        graph.insertEdge(1, 6, 1);
        graph.insertEdge(5, 6, 1);
        graph.insertEdge(2, 3, 1);
        graph.insertEdge(3, 4, 1);
        graph.insertEdge(4, 5, 1);
        graph.insertEdge(6, 7, 1);
        graph.insertEdge(3, 7, 1);
        graph.insertEdge(3, 6, 1);
        System.out.println("结点个数:"+graph.getNumOfVertex());
        System.out.println("边个数:"+graph.getNumOfEdges());
//        graph.depthFirstSearch();                
//        System.out.println(graph.count);
        graph.broadFirstSearch();
        System.out.println(graph.count);
    }

}

结果：

DFS
结点个数:9
边个数:12
A
B
C
D
E
F
G
H
I
重新选择结点次数:1

BFS
结点个数:9
边个数:12
A 
B 
F 
C 
D 
E 
G 
H 
I 
重新选择结点次数:5