经典例题|约瑟夫环多方法解决

Posted 2021-01-29 piuxw

本文章将用循环链表、数组、递归以及循环方法对约瑟夫环问题进行讲解。其中链表法和数组法会对过程进行模拟，递归和循环将对约瑟夫环问题进行数学剖析。

问题描述

n个人围成圈，依次编号为1、2、3、...、n,从1号开始依次报数，当报到m时，报m的人退出，下一个人重新从1报起，当报到m时，报m的人退出，如此循环下去，问最后剩下的那个人的编号是多少？

链表法

建立一个循环链表，节点的数值部分存储整数1至n，将尾部节点链接到第一个节点,每次遍历m-2步，把第m-1个节的指针域指向的节点数据打印出来,然后将m--1这个节点的指针域指向m的指针域指向的节点,再用free将m这个节点内存释放.当只剩一个节点时,（只剩一个节点的判断方法是：节点的指向节点自己，也就是p->next=p）,节点的数值部分就是最后那个人的编号。
代码附上

#include<stdio.h>
#include<stdlib.h>
typedef struct list1{
    int data;
    struct list1 *next;
}list;                          //声明一个链表节点
void func(int ,int ,list *);
void stamp(list *);
int main()
{
    int n,m;
    printf("请输入总人数、出列序号
");
    scanf("%d%d",&n,&m);
    list *l=NULL;
    list *k;
    for(int i=n;i>=1;i--)                           //创建链表
    {
        list *p=(list *)malloc(sizeof(list));
        if(i==n)        k=p;
        p->data=i;
        p->next=l;
        l=p;
    }
        k->next=l;                          //将尾节点链接到第一个节点
        func(n,m,l);
        return 0;
}
void func(int n,int m,list *l)
{
    int num=n;
    stamp(l);
    while(l->next!=l)
    {
        for(int i=1;i<m-1;i++)
        {
        l=l->next;
        }
        printf("*********%d号出列*********
",l->next->data);
        l->next=l->next->next;
        l=l->next;
        num--;
        if(num>1) stamp(l);
        else printf("%d号选手胜出",l->data);
    }
}
void stamp(list *l)                             //每次排除一个人就输出剩余人数(方便理解过程)
{
    list *temp=l;
    printf("剩下的选手为
");
    do
    {
        printf("%d ",temp->data);
        temp=temp->next;
    }while(temp!=l);
    putchar(‘
‘);
} 

数组法

和链表法相似,数组法也是模拟过程.用i来模拟当前人物对应相应数组下标,当i超出剩下人数时,i重归于0,即回到第一个人,从而达到循环的效果,s模拟当前已经历过的人数,当s==m时即淘汰当前人物,将数组从i这个位置往前移动,实现删除这个人的效果

#include<stdio.h>
void func(int n  ,int m );
int main()
{
    int m,n;
    printf("请输入共有多少人,出列编号
");
    scanf("%d%d",&n,&m);            //n人数,m报到出列的号码
        func(n,m);
}
void func(int n,int m)
{
    int a[n],num=n,i,k;                     //num记录当前剩余人数
    for(i=0;i<n;i++)
        a[i]=i+1;
    i=0;    
    while(num>1)
    {
        int s=0;                                //记录已经越过几个人
        for(;;i++)
        {
            if(i==num)
                i=0;
            s++;
            if(s==m)    break;                  //执行删除
        }
        printf("***********%d号出局***********
",a[i]);
        for(int j=i;j<num;j++)                  //删除当前人
            a[j]=a[j+1];                
        num--;
    }
    printf("%d号胜出
",a[0]);             结束
}

数学法(递归.循环)

这个需要数学分析:
假如有6个人,编号为0,1,2,3,4,5,每次报到3的人出列(n=6,m=3);来模拟一下这个过程
第一次淘汰后 0,1,3,4,5 (1)
由于下一次是从3号开始我们可以改写为 3,4,0,1,2 (2)
第二次淘汰后 3,4,0,1 (1)
同理:我们可以改写为 0,1,2,3 (2)
第三次淘汰后 0,1,3 (1)
同理:我们可以改写为 1,2,0 (2)
第四次淘汰后 0,1 (1)
同理:我们可以改写为 0,1 (2)
第五次 1 (1)
改写为 0 (2)
通过观察,发现(1)式可由二式推导出来 例如第五次 ((2)+3)%2
第四次 ((2)+3)%3
......
第一次 ((2)+3)%6
可以发现规律就是(1)式可以由((2)+m)%x x为本轮剩余人数
这样的话我们可以利用递推来解决这个问题.无论你怎么淘汰最后一个剩下的人在(2)式的情况下一定是0,所以可以利用这个规律不断向前得到他原来的序号-1,因为我们是从0开始排序的,但是题目是从1开始排序的.验证一下
(0+3)%2=1,(1+3)%3=1,(1+3)%4=0,(0+3)%5=3,(3+3)%6=0;0+1=1,所以剩下的人应该为1,大家可以用笔验算是不是1,答案肯定是的.这样就可以写程序了.因为取余可能会得到0这个序号,所以我们排序从0开始排,就不用进行其他转化了

递归法

#include<stdio.h>
int func(int ,int );
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    printf("%d",func(n,m)+1);               //得到的数加1就是需要的序号
    return 0;
}
int func(int n,int m)
{
    if(n==1)                                //还剩一个人的时候返回0
        return 0;
    else return (func(n-1,m)+m)%n;      //还剩n个人时就返回((2)+m)%n这个数
}

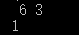
运行结果,正确

循环法

我们利用递归由于不能及时清理现场会占用大量的资源,所以数据较大时会给计算机带来较大负荷,所以得换一个法子,就用循环将递归改造一下就行,因为循环一次清理一次现场,就不会出现上述现象

#include <stdio.h> 
int main()  
{  
    int n,m,i,s=0;
    while( scanf("%d%d",&n,&m)==2)
    {
        s=0;
        for (i=2; i<n; i++)             //递归往里面进去,则循环从里面出来,用i代表剩余人数
            s=(s+m)%i;  
        printf ("%d",s+1);              //输出结果
    }
    return 0 ;  
}  

运行结果,大家可以验算一下,是没有错误的.经过一番推理长代码就剩下了几行,可见算法是十分重要的,但是当题目要求输出每一层被淘汰的人的话,这个程序就不适用的,可见代码各有各的好处,但是要根据题目要求来.
看了这么几种方法你学会了什么呢,欢迎加入piu小屋c语言学习群 进行交流.

piu小屋|全文结