浅谈并查集

Posted 2021-01-29 xyqwq

本文将介绍并查集的模板以及各类问题中的应用

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受;即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果，只能用并查集来描述。

并查集可以算是很基础的结构了，可以快速查找一个元素在哪个集合中，算法模板大致为三大块：
1.Set(初始化)
2.Find(找到元素的祖先)
3.Union(合并两个集合)
因为Union是C艹关键字所以代码中以Merge代替

---

1.Set
建立新集合，各集合初始时不相交。如果用fa[]数组记录某个元素的父亲，即(f_i=j) i的父亲为j，那么初始化时每个元素的父亲指向自己，也就是说有(n)个集合

    void Set(int n)
    {
        for(int i=1; i<=n; ++i)
            fa[i]=i;
        return ;
    }

2.Find

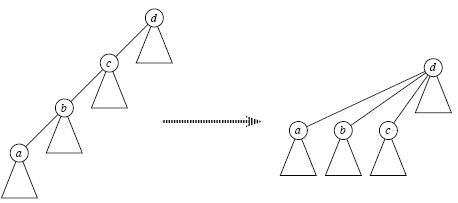
查找元素(x)的根节点，也就是不断向上找爸爸，直到寻找到某个元素(root)的父亲指向自己时，(root)就是这个集合的根。即(root)找不到爸爸了，它便是(x)所在集合的祖宗。
可是如果集合内元素很多，并且以链状排列(如上左图)，每一次都递归找祖宗很浪费时间，我们就需要路径压缩了(如上右图)。

所谓路径压缩，就是在Find的查找路径上把每个节点都直接指向根节点，这样下次再找根节点的时间复杂度会变成O(1)：

    int Find(int x)
    {
        if(fa[x] == x) return x;
        return fa[x]=(Find(fa[x])); //不断更新元素x的爸爸，同时向上寻找祖宗
    }

3.Union

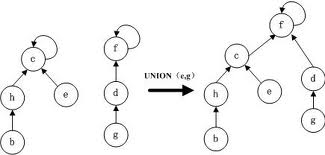
把两个集合合并在一起，我们可以将一个集合的祖宗的父亲指向另外一个集合的祖宗，此时集合数减一

    void Merge(int x, int y)
    {
        int root1=Find(x), root2=Find(y);
        if(root1 == root2) return ; //如果是一个集合就不用合并
        fa[root1]=root2; return ;
    }

$ $

那么并查集的模板就差不多长这样：

namespace Union_Find
{
    void Set(int n)
    {
        for(int i=1; i<=n; ++i)
            fa[i]=i;
        return ;
    }
    int Find(int x)
    {
        if(fa[x] == x) return x;
        return fa[x]=(Find(fa[x]));
    }
    void Merge(int x, int y)
    {
        int root1=Find(x), root2=Find(y);
        if(root1 == root2) return ;
        fa[root1]=root2; return ;
    }
}

using namespace Union_Find;

---

模板例题：
并查集模板
亲戚