SA：利用SA算法解决TSP(数据是14个虚拟城市的横纵坐标)问题——Jason niu

Posted 2020-10-26 yunyaniu

%SA：利用SA算法解决TSP(数据是14个虚拟城市的横纵坐标)问题——Jason niu 
X = [16.4700   96.1000
     16.4700   94.4400
     20.0900   92.5400
     22.3900   93.3700
     25.2300   97.2400
     22.0000   96.0500
     20.4700   97.0200
     17.2000   96.2900
     16.3000   97.3800
     14.0500   98.1200
     16.5300   97.3800
     21.5200   95.5900
     19.4100   97.1300
     20.0900   92.5500];


D = Distance(X);  
N = size(D,1);    

T0 = 1e10;     
Tend = 1e-30; 
L = 2;        
q = 0.9;      
Time = ceil(double(solve([num2str(T0) ‘*(0.9)^x = ‘,num2str(Tend)])));  
count = 0;            
Obj = zeros(Time,1);  
track = zeros(Time,N); 

S1 = randperm(N);  
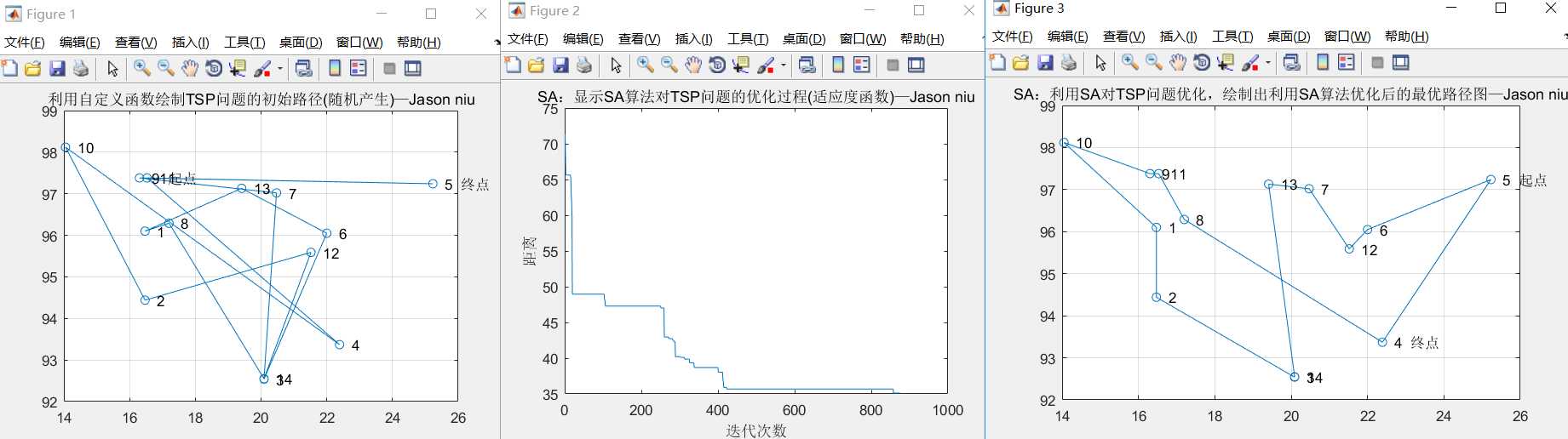
DrawPath(S1,X)     
title(‘利用自定义函数绘制TSP问题的初始路径(随机产生)—Jason niu‘)
disp(‘初始种群中的一个随机值:‘)
OutputPath(S1);    
Rlength = PathLength(D,S1); 
disp([‘总距离：‘,num2str(Rlength)]);

while T0 > Tend    
    count = count + 1;     
    temp = zeros(L,N+1);

    S2 = NewAnswer(S1);  

    [S1,R] = Metropolis(S1,S2,D,T0); 

    if count == 1 || R < Obj(count-1)
        Obj(count) = R;           
    else
        Obj(count) = Obj(count-1);
    end
    track(count,:) = S1;
    T0 = q * T0;         
end

figure
plot(1:count,Obj)
xlabel(‘迭代次数‘)
ylabel(‘距离‘)
title(‘SA：显示SA算法对TSP问题的优化过程(适应度函数)—Jason niu‘)

DrawPath(track(end,:),X)
title(‘SA：利用SA对TSP问题优化，绘制出利用SA算法优化后的最优路径图—Jason niu‘)
%% IX. 输出最优解的路线和总距离
disp(‘最优解:‘)
S = track(end,:);
p = OutputPath(S);
disp([‘总距离：‘,num2str(PathLength(D,S))]);