数据结构开发(20)：树中结点的查找插入清除与删除操作

Posted pylearn

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构开发(20)：树中结点的查找插入清除与删除操作相关的知识，希望对你有一定的参考价值。

0.目录

1.树中结点的查找操作

2.树中结点的插入操作

3.树中结点的清除操作

4.树中结点的删除操作

5.小结

1.树中结点的查找操作

查找的方式：

  • 基于数据元素值的查找
    1. GTreeNode<T>* find(const T& value) const
  • 基于结点的查找
    1. GTreeNode<T>* find(TreeNode<T>* node) const

树中数据元素和结点的查找：
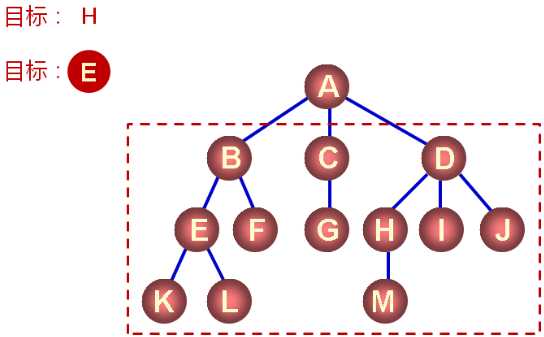
技术分享图片

基于数据元素值的查找：

  • 定义功能：find(node, value)
    1. 在 node 为根结点的树中查找 value 所在的结点

技术分享图片

在GTree.h中实现基于数据元素值的查找：

protected:
    GTreeNode<T>* find(GTreeNode<T>* node, const T& value) const
    {
        GTreeNode<T>* ret = NULL;

        if( node != NULL )
        {
            if( node->value == value )
            {
                return node;
            }
            else
            {
                for(node->child.move(0); !node->child.end() && (ret == NULL); node->child.next())
                {
                    ret = find(node->child.current(), value);
                }
            }
        }

        return ret;
    }
public:
    GTreeNode<T>* find(const T& value) const
    {
        return find(root(), value);
    }

基于结点的查找：

  • 定义功能：find(node, obj)
    1. 在 node 为根结点的树中查找是否存在 obj 结点

技术分享图片

在GTree.h中实现基于结点的查找：

protected:
    GTreeNode<T>* find(GTreeNode<T>* node, GTreeNode<T>* obj) const
    {
        GTreeNode<T>* ret = NULL;

        if( node == obj )
        {
            return node;
        }
        else
        {
            if( node != NULL )
            {
                for(node->child.move(0); !node->child.end() && (ret == NULL); node->child.next())
                {
                    ret = find(node->child.current(), obj);
                }
            }
        }

        return ret;
    }
public:
    GTreeNode<T>* find(TreeNode<T>* node) const
    {
        return find(root(), dynamic_cast<GTreeNode<T>*>(node));
    }

2.树中结点的插入操作

插入的方式：

  • 插入新结点
    1. bool insert(TreeNode<T>* node)
  • 插入数据元素
    1. bool insert(const T& value, TreeNode<T>* parent)

问题：

  • 如何指定新结点在树中的位置？

问题分析：

  • 树是非线性的，无法采用下标的形式定位数据元素
  • 每一个树结点都有唯一的前驱结点 ( 父结点 )
  • 因此，必须先找到前驱结点，才能完成新结点的插入

新结点的插入：
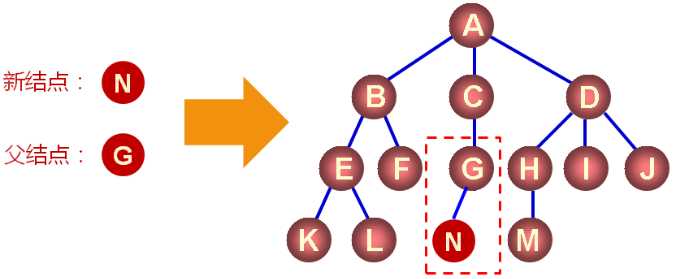
技术分享图片

插入新结点：
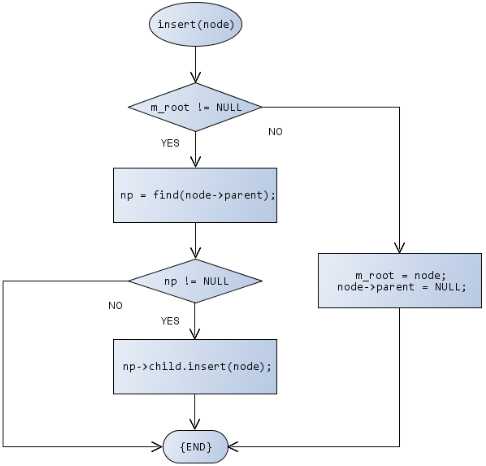
技术分享图片

插入数据元素：
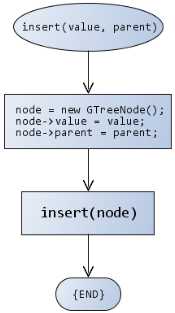
技术分享图片

在GTree.h中实现插入操作：

public:
    bool insert(TreeNode<T>* node)
    {
        bool ret = true;

        if( node != NULL )
        {
            if( this->m_root == NULL )
            {
                node->parent = NULL;
                this->m_root = node;
            }
            else
            {
                GTreeNode<T>* np = find(node->parent);

                if( np != NULL )
                {
                    GTreeNode<T>* n = dynamic_cast<GTreeNode<T>*>(node);

                    if( np->child.find(n) < 0 )
                    {
                        np->child.insert(n);
                    }
                }
                else
                {
                    THROW_EXCEPTION(InvalidOperationException, "Invalid parent tree node ...");
                }
            }
        }
        else
        {
            THROW_EXCEPTION(InvalidParameterException, "Parameter node cannot be NULL ...");
        }

        return ret;
    }

    bool insert(const T& value, TreeNode<T>* parent)
    {
        bool ret = true;
        GTreeNode<T>* node = new GTreeNode<T>();

        if( node != NULL )
        {
            node->value = value;
            node->parent = parent;

            insert(node);
        }
        else
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree node ...");
        }

        return ret;
    }

mian.cpp测试这棵树：
技术分享图片

#include <iostream>
#include "GTree.h"

using namespace std;
using namespace StLib;

int main()
{
    GTree<char> t;
    GTreeNode<char>* node = NULL;

    t.insert(‘A‘, NULL);

    node = t.find(‘A‘);
    t.insert(‘B‘, node);
    t.insert(‘C‘, node);
    t.insert(‘D‘, node);

    node = t.find(‘B‘);
    t.insert(‘E‘, node);
    t.insert(‘F‘, node);

    node = t.find(‘E‘);
    t.insert(‘K‘, node);
    t.insert(‘L‘, node);

    node = t.find(‘C‘);
    t.insert(‘G‘, node);

    node = t.find(‘G‘);
    t.insert(‘N‘, node);

    node = t.find(‘D‘);
    t.insert(‘H‘, node);
    t.insert(‘I‘, node);
    t.insert(‘J‘, node);

    node = t.find(‘H‘);
    t.insert(‘M‘, node);

    const char* s = "KLFGMIJ";

    for(int i=0; i<7; i++)
    {
        TreeNode<char>* node = t.find(s[i]);

        while( node != NULL )
        {
            cout << node->value << " ";

            node = node->parent;
        }

        cout << endl;
    }

    return 0;
}

运行结果为：

K E B A 
L E B A 
F B A 
G C A 
M H D A 
I D A 
J D A

3.树中结点的清除操作

清除操作的定义：

  • void clear()
    1. 将树中的所有结点清除 ( 释放堆中的结点 )

树中数据元素的清除：
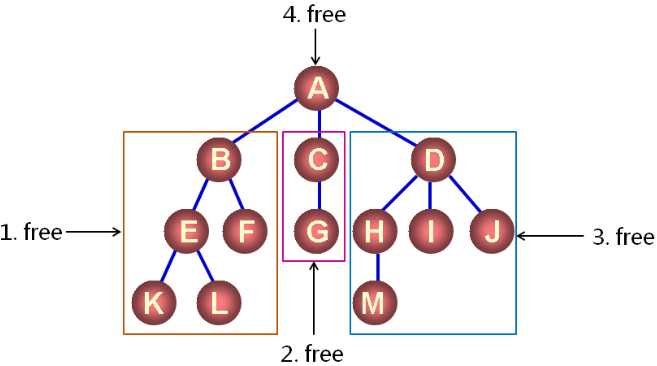
技术分享图片

清除操作功能的定义：

  • free(node)
    1. 清除 node 为根结点的树
    2. 释放树中的每一个结点

技术分享图片

在GTree.h中实现清除操作：

protected:
    void free(GTreeNode<T>* node)
    {
        if( node != NULL )
        {
            for(node->child.move(0); !node->child.end(); node->child.next())
            {
                free(node->child.current());
            }

            delete node;
        }
    }
public:
    void clear()
    {
        free(root());

        this->m_root = NULL;
    }

问题：

  • 树中的结点可能来源于不同的存储空间，如何判断堆空间中的结点并释放？

问题分析

  • 单凭内存地址很难准确判断具体的存储区域
  • 只有堆空间的内存需要主动释放 ( delete )
  • 清除操作时只需要对堆中的结点进行释放

解决方案：工厂模式

  1. 在 GTreeNode 中增加保护成员变量 m_flag
  2. 将 GTreeNode 中的 operator new 重载为保护成员函数
  3. 提供工厂方法 GTreeNode
  4. 在工厂方法中 new 新结点并将 m_flag 设置为 true

树结点的工厂模式示例：
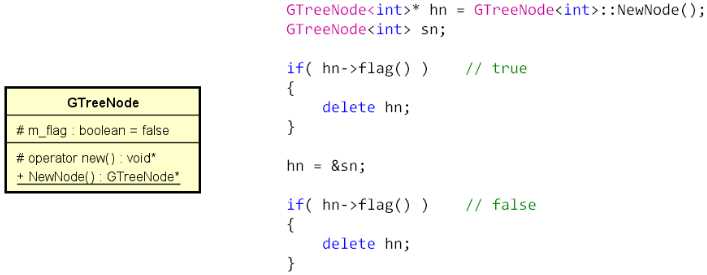
技术分享图片

实现树结点的工厂模式（修改GTreeNode.h和GTree.h中的对应代码）：
GTreeNode.h

#ifndef GTREENODE_H
#define GTREENODE_H

#include "Tree.h"
#include "LinkList.h"

namespace StLib
{

template <typename T>
class GTreeNode : public TreeNode<T>
{
protected:
    bool m_flag;

    void* operator new(size_t size) throw()
    {
        return Object::operator new(size);
    }
public:
    LinkList<GTreeNode<T>*> child;

    GTreeNode()
    {
        m_flag = false;
    }

    bool flag()
    {
        return m_flag;
    }

    static GTreeNode<T>* NewNode()
    {
        GTreeNode<T>* ret = new GTreeNode<T>();

        if( ret != NULL )
        {
            ret->m_flag = true;
        }

        return ret;
    }
};

}

#endif // GTREENODE_H

修改GTree.h中的对应代码：

protected:
    void free(GTreeNode<T>* node)
    {
        if( node != NULL )
        {
            for(node->child.move(0); !node->child.end(); node->child.next())
            {
                free(node->child.current());
            }

            if( node->flag() )
            {
                delete node;
            }
        }
    }
public:
    bool insert(const T& value, TreeNode<T>* parent)
    {
        bool ret = true;
        GTreeNode<T>* node = GTreeNode<T>::NewNode();

        if( node != NULL )
        {
            node->value = value;
            node->parent = parent;

            insert(node);
        }
        else
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree node ...");
        }

        return ret;
    }

4.树中结点的删除操作

删除的方式：

  • 基于数据元素值的删除
    1. SharedPointer< Tree<T> > remove(const T& value)
  • 基于结点的删除
    1. SharedPointer< Tree<T> > remove(TreeNode<T>* node)

删除操作成员函数的设计要点：

  • 将被删结点所代表的子树进行删除
  • 删除函数返回一棵堆空间中的树
  • 具体返回值为指向树的智能指针对象

树中结点的删除：
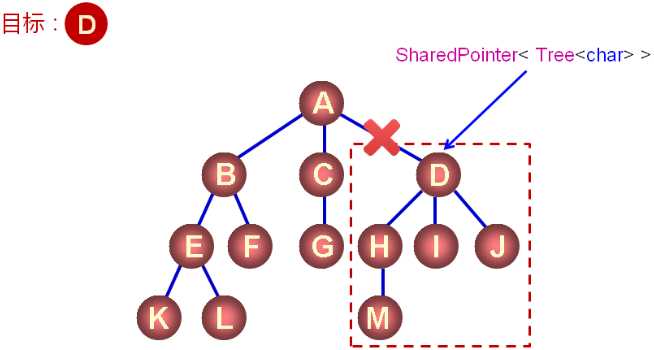
技术分享图片

实用的设计原则：

  • 当需要从函数中返回堆中的对象时，使用智能指针 ( SharedPointer ) 作为函数的返回值。

删除操作功能的定义：

  • void remove(GTreeNode<T>* node, GTree<T>*& ret)
    1. 将 node 为根结点的子树从原来的树中删除
    2. ret 作为子树返回 ( ret 指向堆空间中的树对象 )

删除功能函数的实现：
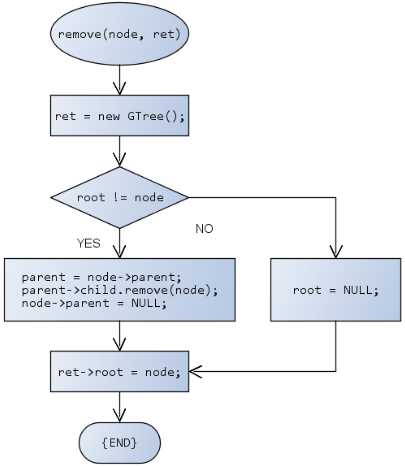
技术分享图片

在GTree.h中实现删除操作：

protected:
    void remove(GTreeNode<T>* node, GTree<T>*& ret)
    {
        ret = new GTree<T>();

        if( ret == NULL )
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree ...");
        }
        else
        {
            if( root() == node )
            {
                this->m_root = NULL;
            }
            else
            {
                LinkList<GTreeNode<T>*>& child = dynamic_cast<GTreeNode<T>*>(node->parent)->child;

                child.remove(child.find(node));

                node->parent = NULL;
            }

            ret->m_root = node;
        }
    }
public:
    SharedPointer< Tree<T> > remove(const T& value)
    {
        GTree<T>* ret = NULL;
        GTreeNode<T>* node = find(value);

        if( node == NULL )
        {
            THROW_EXCEPTION(InvalidParameterException, "Can not find the node via parameter value ...");
        }
        else
        {
            remove(node, ret);
        }

        return ret;
    }

    SharedPointer< Tree<T> > remove(TreeNode<T>* node)
    {
        GTree<T>* ret = NULL;

        node = find(node);

        if( node == NULL )
        {
            THROW_EXCEPTION(InvalidParameterException, "Parameter node is invalid ...");
        }
        else
        {
            remove(dynamic_cast<GTreeNode<T>*>(node), ret);
        }

        return ret;
    }

main.cpp测试

#include <iostream>
#include "GTree.h"

using namespace std;
using namespace StLib;

int main()
{
    GTree<char> t;
    GTreeNode<char>* node = NULL;
    GTreeNode<char> root;

    root.value = ‘A‘;
    root.parent = NULL;

    t.insert(&root);

    node = t.find(‘A‘);
    t.insert(‘B‘, node);
    t.insert(‘C‘, node);
    t.insert(‘D‘, node);

    node = t.find(‘B‘);
    t.insert(‘E‘, node);
    t.insert(‘F‘, node);

    node = t.find(‘E‘);
    t.insert(‘K‘, node);
    t.insert(‘L‘, node);

    node = t.find(‘C‘);
    t.insert(‘G‘, node);

    node = t.find(‘G‘);
    t.insert(‘N‘, node);

    node = t.find(‘D‘);
    t.insert(‘H‘, node);
    t.insert(‘I‘, node);
    t.insert(‘J‘, node);

    node = t.find(‘H‘);
    t.insert(‘M‘, node);

    SharedPointer< Tree<char> > p = t.remove(t.find(‘D‘));

    const char* s = "KLFGMIJ";

    for(int i=0; i<7; i++)
    {
        TreeNode<char>* node = p->find(s[i]);

        while( node != NULL )
        {
            cout << node->value << " ";

            node = node->parent;
        }

        cout << endl;
    }

    return 0;
}

运行结果为：





M H D 
I D 
J D

5.小结

  • 查找操作是树的关键操作之一
  • 基于数据元素的查找可判断值是否存在于树中
  • 基于结点的查找可判断树中是否存在指定结点
  • 插入操作和删除操作都依赖于查找操作
  • 插入操作是构建树的唯一操作
  • 执行插入操作时必须指明结点间的父子关系
  • 插入操作必须正确处理指向父结点的指针
  • 插入数据元素时需要从堆空间中创建结点
  • 清除操作用于销毁树中的每个结点
  • 销毁结点时需要决定是否释放对应的内存空间
  • 工厂模式可用于“定制”堆空间中的结点
  • 只有销毁定制结点的时候需要进行释放
  • 删除操作将目标结点所代表的子树移除
  • 删除操作必须完善处理父结点和子结点的关系
  • 删除操作的返回值为指向树的智能指针对象
  • 函数中返回堆中的对象时，使用智能指针作为返回值

最终的GTreeNode.h和GTree.h代码：
GTreeNode.h

#ifndef GTREENODE_H
#define GTREENODE_H

#include "Tree.h"
#include "LinkList.h"

namespace StLib
{

template <typename T>
class GTreeNode : public TreeNode<T>
{
protected:
    bool m_flag;

    void* operator new(size_t size) throw()
    {
        return Object::operator new(size);
    }
public:
    LinkList<GTreeNode<T>*> child;

    GTreeNode()
    {
        m_flag = false;
    }

    bool flag()
    {
        return m_flag;
    }

    static GTreeNode<T>* NewNode()
    {
        GTreeNode<T>* ret = new GTreeNode<T>();

        if( ret != NULL )
        {
            ret->m_flag = true;
        }

        return ret;
    }
};

}

#endif // GTREENODE_H

GTree.h

#ifndef GTREE_H
#define GTREE_H

#include "Tree.h"
#include "GTreeNode.h"
#include "Exception.h"

namespace StLib
{

template <typename T>
class GTree : public Tree<T>
{
protected:
    GTreeNode<T>* find(GTreeNode<T>* node, const T& value) const
    {
        GTreeNode<T>* ret = NULL;

        if( node != NULL )
        {
            if( node->value == value )
            {
                return node;
            }
            else
            {
                for(node->child.move(0); !node->child.end() && (ret == NULL); node->child.next())
                {
                    ret = find(node->child.current(), value);
                }
            }
        }

        return ret;
    }

    GTreeNode<T>* find(GTreeNode<T>* node, GTreeNode<T>* obj) const
    {
        GTreeNode<T>* ret = NULL;

        if( node == obj )
        {
            return node;
        }
        else
        {
            if( node != NULL )
            {
                for(node->child.move(0); !node->child.end() && (ret == NULL); node->child.next())
                {
                    ret = find(node->child.current(), obj);
                }
            }
        }

        return ret;
    }

    void free(GTreeNode<T>* node)
    {
        if( node != NULL )
        {
            for(node->child.move(0); !node->child.end(); node->child.next())
            {
                free(node->child.current());
            }

            if( node->flag() )
            {
                delete node;
            }
        }
    }

    void remove(GTreeNode<T>* node, GTree<T>*& ret)
    {
        ret = new GTree<T>();

        if( ret == NULL )
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree ...");
        }
        else
        {
            if( root() == node )
            {
                this->m_root = NULL;
            }
            else
            {
                LinkList<GTreeNode<T>*>& child = dynamic_cast<GTreeNode<T>*>(node->parent)->child;

                child.remove(child.find(node));

                node->parent = NULL;
            }

            ret->m_root = node;
        }
    }
public:
    bool insert(TreeNode<T>* node)
    {
        bool ret = true;

        if( node != NULL )
        {
            if( this->m_root == NULL )
            {
                node->parent = NULL;
                this->m_root = node;
            }
            else
            {
                GTreeNode<T>* np = find(node->parent);

                if( np != NULL )
                {
                    GTreeNode<T>* n = dynamic_cast<GTreeNode<T>*>(node);

                    if( np->child.find(n) < 0 )
                    {
                        np->child.insert(n);
                    }
                }
                else
                {
                    THROW_EXCEPTION(InvalidOperationException, "Invalid parent tree node ...");
                }
            }
        }
        else
        {
            THROW_EXCEPTION(InvalidParameterException, "Parameter node cannot be NULL ...");
        }

        return ret;
    }

    bool insert(const T& value, TreeNode<T>* parent)
    {
        bool ret = true;
        GTreeNode<T>* node = GTreeNode<T>::NewNode();

        if( node != NULL )
        {
            node->value = value;
            node->parent = parent;

            insert(node);
        }
        else
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree node ...");
        }

        return ret;
    }

    SharedPointer< Tree<T> > remove(const T& value)
    {
        GTree<T>* ret = NULL;
        GTreeNode<T>* node = find(value);

        if( node == NULL )
        {
            THROW_EXCEPTION(InvalidParameterException, "Can not find the node via parameter value ...");
        }
        else
        {
            remove(node, ret);
        }

        return ret;
    }

    SharedPointer< Tree<T> > remove(TreeNode<T>* node)
    {
        GTree<T>* ret = NULL;

        node = find(node);

        if( node == NULL )
        {
            THROW_EXCEPTION(InvalidParameterException, "Parameter node is invalid ...");
        }
        else
        {
            remove(dynamic_cast<GTreeNode<T>*>(node), ret);
        }

        return ret;
    }

    GTreeNode<T>* find(const T& value) const
    {
        return find(root(), value);
    }

    GTreeNode<T>* find(TreeNode<T>* node) const
    {
        return find(root(), dynamic_cast<GTreeNode<T>*>(node));
    }

    GTreeNode<T>* root() const
    {
        return dynamic_cast<GTreeNode<T>*>(this->m_root);
    }

    int degree() const
    {
        return 0;
    }

    int count() const
    {
        return 0;
    }

    int height() const
    {
        return 0;
    }

    void clear()
    {
        free(root());

        this->m_root = NULL;
    }

    ~GTree()
    {
        clear();
    }
};

}

#endif // GTREE_H











以上是关于数据结构开发(20)：树中结点的查找插入清除与删除操作的主要内容，如果未能解决你的问题，请参考以下文章

第六十四课 二叉树中结点的删除与清除

二叉排序树中插入一个结点的时间复杂度是多少

数据结构 c语言版 ——顺序表的查找、插入与删除

了解数据结构之平衡二叉树 （AVL）-插入和删除

二叉排序树

20172313 2018-2019-1 《程序设计与数据结构》第七周学习总结