scheme 之门
Posted lsgxeva
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了scheme 之门相关的知识,希望对你有一定的参考价值。
scheme 之门
来源 https://www.cnblogs.com/jiyuan-k/p/7482572.html
开始之前
这是一篇 Scheme 的介绍文章. Scheme 是一个 LISP 的方言, 相对于 Common LISP 或其他方言, 它更强调理论的完整和优美, 而不那么强调实用价值. 我在 学习 Scheme 的时候, 常想的不是 "这有什么用", 而是 "为什么" 和 "它 的本质是什么". 我觉得这样的思考对学习计算机是非常有益的.
我不知道 "Scheme 之道" 这个题目是否合适, 我还没到能讲 "XXX 之道" 的时候. 但 Scheme 确实是一个极具哲学趣味的语言, 它往往专注于找出事物的 本质, 用最简单, 最通用的方法解决问题. 这样的思路下, 我们会碰到许多以往 不会遇到, 或不甚留意的问题, 使我们对这些问题, 以及计算机科学的其他方面 有新的认识和思考.
讲 Scheme 的好书有很多, 但 Scheme 在这些书中往往就像指着月亮的慧能的手 指或是道家的拂尘, 指引你发现计算机科学中的某些奇妙之处, 但 Scheme 本身 却不是重点. 如SICP (Structure and Interpretation of Computer Programs) 用 Scheme 来指引学生学习计算机科学中的基本概念; HTDP (How to design programs) 用Scheme 来介绍程序设计中常用的技巧和方法. 而这篇文章, 着眼点 也不是scheme 本身, 或者着眼点不在 scheme 的 "形", 而在与 scheme 的 "神". 怎么写一个好的 scheme 程序不是我的重点, 我的重点是 "这个设计真 美妙", "原来本质就是如此", 如是而已. Scheme 的一些理论和设计启发了我 , 使我在一些问题, 一些项目上有了更好的想法. 感念至今, 所以写一系列小文 将我的体会与大家分享.
要体验 Scheme, 当然首先要一个 Scheme 的编程环境. 我推荐 drScheme (http://www.drscheme.org), 跨平台, 包括了一个很好的编辑和调试界面 . Debian/Ubuntu 用户直接 apt-get 安装即可.
希望读者有基本的编程和数据结构知识. 因为解释 Scheme 的很多概念时, 这些 知识是必须的.
数据结构的本质论
世界的终极问题
这两个可能是人类对世界认识的终极问题: 世界上最基本的, 不可再分的物质单 位是什么? 这些最基本的物质单位是怎么组成这个大千世界的?
Scheme 也在试图解答这个问题.
Scheme 认为以下两种东西是原子性的, 不可再分的: 数, 符号. 数这个好理解, 符号这个概念就有点麻烦了. 做个比方, "1" 是一个数字, 但它其实是一个符 号, 我们用这个符号去代表 "1" 这个概念, 我们也可以用 "一" 或 "one" 代表这个概念, 当然 "1" 也可以表示 "真" 的概念, 或者什么都 不表示. 而 kyhpudding 也是一个 Scheme 中的符号, 它可以代表任何东西, Scheme 能理解的或不能理解的. 这都没所谓, Scheme 把它作为一个原子单位对 它进行处理: 1 能跟其他数字作运算得出一个新的数字, 但 1 始终还是 1, 它 不会被分解或变成其他什么东西, 作为符号的 kyhpudding 也大抵如此.
下一个问题是: 怎么将原子组成各种复合的数据结构 --- 有没有一种统一的方 法?
我们从最简单的问题开始: 怎么将两个对象聚合在一起? 于是我们引入了 "对 " (pair) 的概念, 用以聚合两个对象: a 和 b 组成的对, 记为:
如果是要聚合三个或以上的数据呢? pair 的方法还适用吗? 我们是否需要引入 其他方法? 答案是不需要, 我们递归地使用 pair 结构就可以了. 聚合 a, b, c, 记为 (a . (b . c)), 它的简化记法是 (a b . c).
大家都能想到了, 递归地使用 pair 二叉树的结构, 就能表达任意多个对象组成 的序列. 比如 (a b . c), 画图就是:
请大家继续将头左侧 45 度. 这样的一个表示序列的树的特点是, 树的左结点是 成员对象, 右结点指向一颗包含其他成员的子树. 但大家也发现了一个破例: 图 中的 c 是右边的叶子. 解决这个问题的办法是: 我们引入一个 "无" 的概念:
这个无的概念我们用 "()" 来表达 (总不能什么都没有吧). 记 (a . ()) 为 (a). 那么上图就可以表示为 (a b c). 这样的结构我们就叫做列表 --- List. 这是 Scheme/LISP 中应用最广的概念. LISP 其实就是 "LISt Processing" 的意思.
这样的结构表达能力很强, 因为它是可递归的, 它可以表达任何东西. 比方说, 一个普通的二叉树可以像这样表示 (根 (根 左子树 右子树) 右子树). 大家也 可以想想其他的数据结构怎么用这种递归的列表来表示.
开始编程啦
好了, 我们可以开始写一点很简单的 Scheme 程序. 比方说, 打入 1, 它就会返 回 1. 然后, 打入一个列表 (1 2), 出错鸟... 打入一个符号: kyhpudding, 也 出错鸟......
于是我们就要开始讲一点点 Scheme 的运作原理了. 刚才我们讲了 Scheme 中的 数据结构, 其实不但是 Scheme 处理的数据, 整个 Scheme 程序都是由这样的列 表和原子对象构成的, 一个合法的 Scheme 数据结构就是一个 Scheme 语句. 那 么这样的语句是怎么运行的呢? 总结起来就是三条逻辑:
- 如果那是一个数, 则返回这个数
- 如果那是一个符号, 则返回该符号所绑定的对象. (这个概念我们会迟点解释)
- 如果那是一个列表, 把列表的第一项作为方法, 其他作为参数, 执行之.
所以, 我们可以试试这个 (+ 1 2), 这下就能正确执行了.
那么, 如果我就想要他返回 (+ 1 2) 这个列表呢? 试试这样 (quote (+ 1 2)) quote 是一个很特殊的操作, 意思是它的参数不按规则处理, 而是直接作为数据 返回. 我们会常常用到它, 所以也有一个简化的写法 ‘(+ 1 2), 在前面加一个 单引号就可以了. 这样子, ‘kyhpudding 也能有正确的输出了.
那么我们可以介绍三个原子操作, 用以操纵列表. 其实, 所谓操纵列表, 也只是 操纵二叉树而已. 所以我们有这么三个操作:
- cons: 将它的两个参数组合起来, 形成新的二叉树/pair
- car: 返回参数的左子树
- cdr: 返回参数的右子树
通过以下几个操作, 结合对应的二叉树图, 能比较好的理解这个 Scheme 最基础 的设计:
无处不在的函数
基本的函数概念
Scheme 是一门函数式语言, 因为它的函数与数据有完全平等的地位, 它可以在 运行时被实时创建和修改. 也因为它的全部运行都可以用函数的方式来解释, 莫 能例外.
比方说, 把 if 语句作为函数来解释? (if cond if-part else-part) 是这么一 个特殊的函数: 它根据 cond 是否为真, 决定执行并返回 if-part 还是 else-part. 比如, 我可以这样写:
if 函数会根据我开心与否 (i-am-feeling-lucky 是一个由我决定它的返回值的 函数 :P) 返回 + 或 - 来作为对我的开心值的操作. 所谓无处不在的函数, 其 意义大抵如此.
把一串操作序列当成函数呢? Scheme 是没有 "return" 的, 把一串操作序列 当作一个整体, 它的返回值就是这一串序列的最后一个的返回值. 比如我们可以 写
它的返回是 7.
无名的能量之源
接下来, 我们就要接触到 Scheme 的灵魂 --- Lambda. 大家可以注意到 drScheme 的图标, 那就是希腊字母 Lambda. 可以说明 Lambda 运算在 Scheme 中是多么重要.
NOTE: 这里本来应该插一点 Lambda 运算的知识的, 但是一来我自己数学就不怎 么好没什么信心能讲好, 二来讲太深了也没有必要. 大家如果对 Lambda 运算的 理论有兴趣的话, 可以自行 Google 相关资料.
Lambda 能够返回一个匿名的函数. 在这里需要注意两点: 第一, 我用的是 "返 回" 而不是 "定义". 因为 Lambda 同样可以看成一个函数 --- 一个能够生 成函数的函数. 第二, 它是匿名的, 意思是, 一个函数并不一定需要与一个名字 绑定在一起, 我们有时侯需要这么干, 但也有很多时候不需要.
我们可以看一个 Lambda 函数的基本例子:
这里描述了一个加法函数的生成和使用. (lambda (x y) (+ x y)) 中, lambda 的第一个参数说明了参数列表, 之后的描述了函数的行为. 这就生成了一个函数 , 我们再将 1 和 2 作用在这个函数上, 自然能得到结果 3.
我们先引入一个 define 的操作, define 的作用是将一个符号与一个对象绑定 起来. 比如
我们自然也可以用 define 把一个符号和函数绑定在一起, 就得到了我们常用的 有名函数.
做一个简单的替换, 上面的例子就可以写成 (add 1 2), 这样就好理解多了.
上面的写法有点晦涩, 而我们经常用到的是有名函数, 所以我们有一个简单的写 法, 我们把这一类简化的写法叫 "语法糖衣". 在前面我们也遇到一例, 将 (quote x) 写成 ‘x 的例子. 上面的定义, 我们可以这样写
Lambda 运算有极其强大的能力, 上面只不过是用它来做传统的 "定义函数" 的工作. 它的能力远不止如此. 这里只是举几个小小的例子:
我们经常会需要一些用于迭代的函数, 比如这个:
我们也需要减的, 乘的, 还有其他各种乱七八糟的操作, 我们需要每次迭代不是 1, 而是 2, 等等等等. 我们很自然地有这个想法: 我们写个函数来生成这类迭 代函数如何? 在 Scheme 中, 利用 lambda 运算, 这是可行且非常简单的. 因为 在 Scheme 中, 函数跟普通对象是有同样地位的, 而 "定义" 函数的 lambda, 其实是能够动态地为我们创造并返回函数对象的. 所以我们可以这么写:
这个简单的例子, 已经能够完成我们在 C 之类的语言无法完成的事情. 要生成 上面的 inc 函数, 我们可以这么写:
这个例子展示的是 Scheme 利用 Lambda 运算得到的能力. 利用它, 我们可以写 出制造函数的函数, 或者说制造机器的机器, 这极大地扩展了这门语言的能力 . 我们在以后会有更复杂的例子.
接下来, 我们会介绍 Scheme 的一些语言特性是怎么用 Lambda 运算实现的 --- 说 Scheme 的整个机制是由 Lambda 驱动的也不为过.
比如, 在 Scheme 中我们可以在任何地方定义 "局部变量", 我们可以这么写:
其实 let 也只不过是语法糖衣而已, 因为上面的写法等价于:
一些常用的函数
虽然说这篇文章不太注重语言的实用性. 但这里还是列出我们经常用到的一些操 作, 这能极大地方便我们的编程, 大家也可以想想他们是怎么实现的.
cond
相当于 C 中的 switch
循环语句
没有循环语句...... 至少没有必要的循环语句. Scheme 认为, 任何的循环迭代 都可以用递归来实现. 我们也不用担心递归会把栈占满, 因为 Scheme 会自动处 理尾递归的情况. 一个简单的 0 到 10 迭代可以写成这样.
很明显, 当我们递归调用 iterate 的时候, 我们不必保存当前的函数环境. 因 为我们递归调用完毕后就马上返回, 而不会再使用当前的环境, 这是一给尾递归 的例子. Scheme 能自动处理类似的情况甚至做一些优化, 不会浪费多余的空间, 也不会降低效率. 所以完全可以代替循环.
当然我们有些便于循环迭代的操作, 大家可以试试自己实现他们. (当然在解释 器内部通常不会用纯 scheme 语句实现他们). 我们最常用的是 map 操作
运行一下这个例子, 就能理解 map 的作用了.
更多的数据操作
- cadr cddr caddr 之类, 就是 car 和 cdr 的组合, 大家可以一个个试 . drScheme 支持到 cadddr...
- append: 将两个列表拼接在一起.
无始无终的太极
我想其他语言的入门教程都不会有这么一节: 这门语言的运作原理是怎么样的 . 但这么一节内容是 Scheme 的入门教程必有的. Scheme 把它最核心, 最底层 的机制都提供出来给用户使用, 使它有非常强大的能力. 所以知道它的运行机理 是非常重要的.
这一节和下一节都是在分析 Scheme 的运行原理. 在这一节中, 我们会用一个太 极图来分析一条 Scheme 语句是怎么被执行的. 在下一节, 我们会在这一节的基 础上引入 Scheme 的对象/内存管理机制. 从而得到一个比较完整的 Scheme 运 行原理, 并用 Scheme 语言表示出来.
我们先从 eval 和 apply 的用法说起. eval 接受一个参数, 结果是执行那个参 数的语句, 而 apply 则接受两个参数, 第一个参数表示一个函数, 第二个参数 是作用于这个函数的参数列表. 例如:
我们可以轻易发现, 这两者是可以轻易转化的:
但是显然, 真正的实现不可能如此, 不然 eval 一次就没完没了地转圈了. 我们 在前面提到 Scheme 的基本运行逻辑, 其实也是 eval 的基本原理:
- 如果那是一个数, 则返回这个数
- 如果那是一个符号, 则返回该符号所绑定的对象.
- 如果那是一个列表, 把列表的第一项作为方法, 其他作为参数, 执行之.
我们来实现一个这样的逻辑, 要注意的是, 下面的 eval 和 apply 的写法都只 是说明概念, 并不是真实可运行的. 但用 Scheme 写一个 Scheme 解释器是确实 可行的:
在第三项, 我们很自然地用了 apply 来实现. 注意 apply 接受的第一个参数必 须是一个函数对象, 而不能是一个类似 add 的名字, 所以我们要递归地调用 eval 解析出它的第一个参数. 那么 apply 要怎么实现呢? 我们来看一个实例:
用 eval 执行它的时候, 会执行
在执行它的时候 , 为了运行它, 我们要知道 add 和 x 代表什么, 我们还得知道 (+ y 1) 的结果, 否则我们的计算无法继续下去. 我们用什么来求得这些值呢
--- 显然是eval. 因此 apply 的处理流程大致如下:
我们得到的还是一个互相递归的关系. 不过这个递归是有尽头的, 当我们遇到原 子对象时, 在 eval 处就会直接返回, 而不会再进入这个递归. 所以 eval 和 apply 互相作用, 最终把程序解释成原子对象并得到结果. 这种循环不息的互相 作用, 可以表示为这样一个太极:
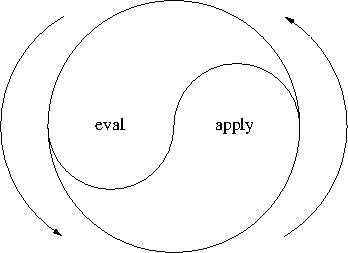
这就是一个 Scheme 解释器的核心.
然而, 我们上面的模型是不尽准确的. 比如, (if cond if-part else-part) 把 这个放入 apply 中的话, if-part 和 else-part 都会被执行一遍, 这显然不是 我们希望的. 因此, 我们需要有一些例外的逻辑来处理这些事情, 这个例外逻辑 通常会放在 eval. (当然理论上放在 apply 里也可以, 大家可以试一下写, 不 过这样在 eval 中也要有特殊的逻辑之处 "if" 这个符号所对应的值). 我们 可以把 eval 改成这样
这样我们的逻辑就比较完整了.
另外 apply 也要做一些改动, 对于 apply 的 method, 它有可能是类似 "+" 这样的内置的 method, 我们叫它做 primitive-proceure, 还有由 lambda 定义 的 method, 他们的处理方法是不一样的.
在下一节, 我们就会从 lambda 函数是怎么执行的讲起, 并再次修改 eval 和 apply 的定义, 使其更加完整. 在这里我们会提到一点点 lambda 函数的执行原 理, 这其实算是一个 trick 吧.
我们这样定义 lambda 函数
那么我们在 apply 这个 lambda 函数的时候会发生什么呢? apply 会根据参数 表和参数做一次匹配, 比如, 参数表是 (x y) 参数是 (1 2), 那么 x 就是 1, y 就是 2. 那么, 我们的参数表写法其实可以非常灵活的, 可以试试这两个语句 的结果:
((lambda x x) 1 2) <= 注意两个 x 都是没有括号的哦 ((lambda (x . y) (list x y)) 1 2 3)
这样 "匹配" 的意义是否会更加清楚呢? 由于这样的机制, 再加上可以灵活运 用 eval 和 apply, 可以使 Scheme 的函数调用非常灵活, 也更加强大.
唯心主义的对象管理系统
关于对象
既然这一节我们要讲对象管理系统. 我们首先就要研究对象, 研究在 Scheme 内 部是如何表示一个对象. 在 Scheme 中, 我们的对象可以分成两类: 原子对象和 pair.
我们要用一种办法唯一地表示一个对象. 对原子对象, 这没什么好说的, 1 就是 1, 2 就是 2. 但是对 pair, 情况就比较复杂了.
如果我们修改了 a 的 car 的值, 我们不希望 b 的值也同样的被改变. 因此虽 然 a 和 b 在 define 时的值一样, 但他们不是相同的对象, 我们要分别表示他 们. 但是 在这个时候
a 和 b 应该指的是同一个对象, 不然 define 的定义就会很尴尬 (define 不是 赋值, 而是绑定). 修改了 a 的 car, b 也应该同时改变.
答案很明显了: 对 pair 对象, 我们应把它表示为一个引用 --- 熟悉 Java 的 同学也会知道一个相同的原则: 在 Java 中, 变量可以是一个原子值 (如数字), 或者是对一个复合对象的引用.
在这里我们引入一组操作, 它可以帮助测试, 理解这样的对象系统:
- set!: 不要漏了叹号, 修改一个符号的绑定
- set-car!: 修改 pair 中左边值的绑定
- set-cdr!: 修改 pair 中右边值的绑定
- eq?: 测试两个对象是否相等
- equal?: 测试两个对象的值是否相等.
我们可以进行如下测试:
另外我们可以想想以下操作形成的对象的结构:
它形成的结构应该是这样的
所以 (eq? (cdr a) (cdr b)) 的值应该是真.
lambda 的秘密
接下来我们要研究: Scheme 是怎么执行一个 lambda 函数的? 运行一个 lambda 函数, 最重要的就是建立一个局部的命名空间, 以支持局部变量 --- 对 Scheme 来说, 所谓局部变量就是函数的参数了. 只要建立好这样的一个命名空间, 剩下 的事情就是在此只上逐条运行语句而已了.
我们首先可以看这样的一个例子:
结果当然是 20, 这说明了 Scheme 在运行 lambda 函数时会建立一个局部的命名 空间 --- 在 Scheme 中, 它叫做 environment, 为了与其他的资料保持一致, 我 们会沿用这个说法, 并把它简写为 env. 而且这个局部 env 有更高的优先权 . 那我们似乎可以把寻找一个符号对应的对象的过程描述如下, 这也是 C 语言程 序的行为:
- 先在函数的局部命名空间里搜索
- 如果找不到, 在全局变量中搜索.
但是 Scheme 中, 函数是可以嵌套的:
很好, 这不就是一个栈的结构吗? 我们在运行中维护一个 env 的栈, 搜索一个名 称绑定时从栈顶搜索到栈底就可以了.
这在 Pascal 等静态语言中是可行的 (Pascal 也支持嵌套的函数定义). 但是在 Scheme 中不行 --- Scheme 的函数是可以动态生成的, 这会产生一些栈无法处 理的情况, 比如我们上面使用过的例子:
执行 inc 和 dec 的时候, 它执行的是 (method x step), x 的值当然很好确定 , 但是method 和 step 的值就有点麻烦了. 我们调用 make-iterator 生成 inc 和dec 的时候, 用的是不同的参数, 执行 inc 和 dec 的时候, method 和 step 的值当然应该不一样, 应该分别等于调用 make-iterator 时的参数. 这样的特性 , 就没法用一个栈的模型来解释了.
一个更令人头痛的问题是: 运行 lambda 函数时会创造一个 env, 现在看起来, 这个 env 不是一个临时性的存在, 即使是在函数执行完以后, 它都有存在的必要 , 不然像上例中, inc 在运行时就没法正确地找到 + 和 1 了. 这是一种我们从 未遇到的模型.
我们要修改函数的定义. 在 Scheme 中, 函数不仅是一段代码, 它还要和一个 environment 相连. 比如, 在调用 (make-iterator + 1) 的时候, 生成的函数要 与执行函数 make-iterator 实时产生的 env 相连, 在这里, method = +, step = 1; 而调用 (make-iterator - 1) 的时候, 生成的函数是在与另一个 env --- 第二次调用 make-iterator 产生的 env 相连, 在这里, method = -, step = 1. 另外, 各个 env 也是相连的. 在执行函数 inc 时, 他会产生一个含有名称 x 的 env, 这个 env 要与跟lambda 函数相连的的 lambda 相连. 这样我们在只 含有 x 的 env 中找不到method, 可以到与其相连的 env 中找. 我们可以画图如 下来执行 (inc 10) 时的 env 关系:
inc: ((x 10)) -> ((method +) (step 1)) -> ((make-iterator 函数体))
这里的最后一项就是我们的全局命名空间, 函数 make-iterator 是与这个空间 相连的.
于是我们可以这样表示一个 env 和一个 lambda 函数对象: 一个 env 是这么一 个二元组 (名称绑定列表 与之相连的上一个 env). 一个 lambda 是一个这样的 三元组: (参数表 代码 env).
由此我们需要修改 eval 和 apply. 解释器运行时, 需要一直保持着一个 "当 前 env". 这个当前 env 应该作为参数放进 eval 和 apply 中, 并不断互相传 递. 在生成一个 lambda 对象时, 我们要这样利用 env:
这样就可以表示 lambda 函数与一个 env 的绑定. 那么我们执行 lambda 函数 的行为可以这么描述:
这样我们就可以完全清楚的解释 make-iterator 的行为了. 在执行 (make-iterator + 1) 时, make-env 生成了这样的一个 new-env:
这个 new-env 会作为参数 env 去调用 eval. 在 eval 执行到 lambda 一句时, 又会以这样的参数来调用 make-lambda, 因此这样的一个 env 就会绑定到这个 lambda 函数上. 同理, 我们调用 (make-iterator - 1) 的时候, 就能得到另一 个 env 的绑定.
这种特性使 "函数" 在 scheme 中的含义非常丰富, 使用非常灵活, 以下这个 例子实现了非常方便调试的函数计数器:
用普通的参数调用 add 时, 它会执行一个正常的加法操作. 但如果调用 (add ‘print), 它就会返回这个函数被执行了多少次. 这样的一个测试用 wrapper 是 完全透明的. 正因为 scheme 函数可以与一个 env, 一堆值相关联, 才能实现这 么一个功能.
自动垃圾收集
我们的问题远未解决.
C 语言中, 局部变量放在栈中, 执行完函数, 栈顶指针一改, 这些局部变量就全 没了. 这好理解得很. 但根据我们上面的分析, Scheme 中的函数执行完后, 它 创造的 env 还不能消失. 这样的话, 不就过一会就爆内存了么......
所以我们需要一个自动垃圾收集系统, 把用不着的内存空间全部收回. 大家可能 都是在 Java 中接触这么一个概念, 但自动垃圾收集系统的祖宗其实是 LISP, Scheme 也继承了这么一个神奇的系统.
自动垃圾收集系统可以以一句唯心主义的话来概括: 如果你没法看到它了, 它就 不存在了. 在 Java 中, 它似乎是一个很神奇的机制, 但在 Scheme 中, 它却简 单无比.
我们引入上下文的概念: 一个上下文 (context), 包括当前执行的语句, 当前 env, 以及上一个与之相连的 context --- 如我们所知, 在调用 lambda 函数时 , 会产生一个新的 env, 但其实它也产生一个新的 context, 包括了 lambda 中 的代码, 新的 env, 以及对调用它的 context 的引用 (这就好比在 x86 中调用 CALL 指令压栈的当前指令地址, 在使用 RET 的时候可以弹出返回正确的地方 ). 它是这样的一个三元组: (code env prev-context). 任何时候, 我们都处于 一个这样的上下文中.
引入这个概念, 是因为一个 context, 说明了任何我们能够访问和以后可能会访 问的对象集合: 正要运行的代码当然是我们能访问的, env 是所有我们能够访问 的变量的集合, 而 prev-context 则说明了我们以后可能能够访问的东西: 在函 数执行完毕返回后, 我们的 context 会恢复到 prev-context, prev-context 包含的内容是我们以后可能访问到的.
如上所述, code, env, 以及 context 本身都可以描述为标准的 LIST 结构, 那 我们所谓能 "看到" 的对象, 就是当前 context 这个大表中的所有内容. 其 他的东西, 都是垃圾, 要被收走.
比如, 我们处在 curr-context 中, 调用 (add 1 2). 那会产生一个新的 new-context, 在执行完 (add 1 2) 后, 我们又回到了 curr-context, 它与 new-context 不会有任何的联系 --- 我们无论如何也不可能在这里访问到执行 add 时的局部变量. 所以执行 add 时产生的 env 之类, 都会被当作垃圾收走.
当我们使用的内存多于某个阈值, 自动垃圾收集机制就会启动. 有了上面的介绍 , 我们会发现这么个机制简单的不值得写出来: 当前的 context 是一个 LIST, 遍历这个 LIST, 把里面的所有对象标记为有用. 然后遍历全部对象, 把没有标 记为有用的对象全部当垃圾回收, 完了. 当然真实实现远远不是如此, 会有很多 的优化, 但它的基本理论就是如此.
好了, 我们要再一次修改 eval, apply 和 run-lambda 的实现, 这次要怎么改 动大家都清楚得很了.
通过这次修改, 我们也可以解释自动处理尾递归为什么是可行的. 我们在上面举 出了一个尾递归的例子:
在 C 语言中, 再新的新手也不会写这种狂吃内存的愚蠢代码, 但在 Scheme 中, 它是很合理的写法 --- 因为有自动垃圾收集.
在每次调用函数的时候, 我们可以做这样的分析, iterate 的递归调用图如下:
(iterate 0) -> (iterate 1) -> (iterate 2) ....
| ^ | ^ |
----+ +----------+ +-------------+
下面的箭头表示函数返回的路径. 如果我们每次的递归调用都是函数体中的最后 一个语句, 就说明: 比如从 (interate 2) 返回到 (iterate 1) 时, 我们什么 都不用干, 又返回到 (iterate 0) 了. 在 iterate 中, 我们每一层递归都符合 这个条件, 所以我们就给它一个捷径:
(iterate 0) -> (interate 1) -> ... (interate 10)
|
<-----------------------------------------+
让他直接返回到调用 (iterate 0) 之前. 在实现上, 我们可以这么做: 比如, 我们处在 (iterate 0) 的 context 中, 调用 (iterate 1). 我们把 (iterate 1) 的 context 中的 prev-context 记为 (iterate 0) 的 prev-context, 而不 是 (iterate 0) 的 context, 就能形成这么一条捷径了. 我们每一层递归都这 么做, 可以看到, 其实每一层递归的 context 中的 prev-context 都是调用 (interate 0) 之前的 context! 所以其实执行 (interate 10) 的时候, 与前面 的 context 没有任何联系, 前面递归产生的 context 都是幽魂野鬼, 内存不足 时随时可以回收, 因此不用担心浪费内存. 而 Scheme 自动完成分析并构造捷径 的过程, 所以在 Scheme 中可以用这样的递归去实现迭代而保持高效.
面向对象的 Scheme
我们可以这样定义一个对象: 对象就是数据和在数据之上的操作的集合.
Scheme 中的 lambda 函数, 不但有代码, 还和一个 environment, 一堆数据相 连 --- 那不就是对象了么. 在 Scheme 中, 确实可以用 lambda 去实现面向对 象的功能. 一个基本的 "类" 的模板是类似这样的:
使用
这样就能很方便地把它和其他语言中的对象对应起来了.
Scheme 虽然没有真正的, 复杂的面向对象概念, 没有继承之类的咚咚, 但 Scheme 能够实现更灵活, 更丰富的面向对象功能. 比如, 我们前面举过的 make-counter 的例子, 它就是一个函数调用计数器的类, 而且, 它能提供完全 透明的接口, 这一点, 其他语言就很难做到了.
创造机器的机器
真实存在的时光机器
在上一节中, 我们引入了 context 的概念, 这个概念代表 scheme 解释器在任 何时刻的运行状态. 如果我们有一种机制, 能够把某个时候的 context 封存起 来, 到想要的时候, 再把它调出来, 这一定会非常有趣 --- 对, 就像游戏中的 存档一样. 如果真有这样的机制, 那就简直是真实存在的时光机器了.
Scheme 还真的有这个机制 --- 它把 context 也看成一个对象, 可以由用户自 由地使用, 这使我们能完成很多 "神奇" 的事情. 在上一节, 我们为了方便理 解, 使用了 "context" 这一叫法, 在这里, 我们恢复它的正式称呼 --- 这一 节, 我们研究 continuation.
我们还是从它的用法说起, continuation 的使用从 call-with-current-continuation 开始, 这个名字长得实在难受, 我们按惯例 一律缩写为 call/cc. call/cc 可以这样使用
它接受一个函数作为参数, 而这个函数的参数就是这个 continuation 对象. 我 们要怎么用这个对象呢? 以下是一个最简单的例子:
大家可以试试它的结果, 与 (+ 1 2) 相同. 这里最重要的一句是 (cont 2). 我 们从一开始就说, Scheme 中的一切都是函数, 在上一节中我们知道, 为了执行一 个函数, 我们创建一个 context (continuation), 那 context 的行为的最终结 果就是返回一个值了. 而 (cont 2) 这样用法相当于是给 cont 这个 continuation 下个断言: 这个 context(continuation) 的返回值就是 2, 不用 再往下算了 --- 我们也可以这么想象, 当解释器运行到 (cont 2) 的时候, 就把 整个 (call/cc ....) 替换成 2, 所以得到我们要的结果.
没什么特别, 对吧. 但这一点点已经能有很重要的应用 --- 我的函数有很多条 语句 (这在 C 等过程式语言中很常见, 在 Scheme 这类语言中倒是少见的), 我 想让它跑到某个点就直接 return; 我需要一个像 try ... catch 这样的例外机 制, 而不想写一个 N 层的 if. 上面的 continuation 用法就已经能做到了, 大 家可以试试写一个 try ... catch 的框架, 很简单的.
老实说, 上面这个一点都不像时光机, 也不见得有多强大. 我们再来点好玩的:
以上这些语句当然不会有执行结果, 因为 call/cc 没有返回任何值给 x, 在 if 语句之后就无法继续下去了. 不过, 在这里我们把这个 continuation 保存成了 一个全局变量 g-cont. 现在我们可以试试: (g-cont 10). 大家可以看到结果了 : 这才是时光机啊, 通过 g-cont, 我们把解释器送回从前, 让 x 有了一个值, 然后重新计算了 let 之中的内容, 得出我们所要的答案.
这样的机制当然不仅仅是好玩的, 它可以实现 "待定参数" 的功能: 有的函数 并不能直接被调用, 因为它的参数可能由不同的调用者提供, 也可能相隔很长时 间才分别提供. 但无论如何, 只要参数一齐, 函数就要马上得到执行 --- 这是 一种非常常见的模块间通讯模式, 但用普通的函数调用方法无法实现, 其他方法 也很难实现得简单漂亮, continuation 却使它变得非常简单. 比如
到我们用类似 (slot-x 10) 的形式提供完整的 x y 参数值后, add 就会正确地 计算. 在这里, add 不用担心是谁, 在什么时候给它提供参数, 而参数的提供者 也不必关心它提供的数据是给哪个函数, 哪段代码使用. 这样, 模块之间的耦合 度就很低, 而依然能简单, 准确地实现功能. 实在非 continuation 不能为也.
不过要注意的是, continuation 并不是真的如游戏的存档一般 --- 我们知道 continuation 的实现, 一个 continuation 只不过是一个简单的对象指针, 它 不会真的复制保存下全部运行状态. 我们保存下一个 continuation, 修改了全 局变量, 然后再回到那个 continuation, 全局变量是不会变回来的. 有了前一 章的知识, 大家很清楚什么才会一直在那里不被改动 --- 这个 continuation 所关联的私有 env 才是不会被改动的.
既然有时光机的特性, continuation 会是一个强力的实现回溯算法的工具. 我们 可以用 continuation 保存一个回溯点, 当我们的搜索走到一个死胡同, 可以退 回上一个保存的回溯点, 选择其他的方案.
比方说, 在 m0 = (4 2 3) 和 m1 = (1 2 3) 中搜索一个组合, 使 m0 < m1, 这 是一个非常简单的搜索问题. 我们递归地先选一个 m0 的值, 再选一个 m1 的值 , 到下一层递归的时候, 由于没有东西可选了. 所以我们检验是否 m0 < m1, 如 果是, 退出, 否则就回溯到上一回溯点, 选择下一个值.
回溯点的保存当然是用 continuation, 我们不但要在一个尝试失败时使用 continuation 作回溯, 还需要在得到正确答案时用 continuation 跳过层层递 归, 直接返回答案.
所以, 我们有这样的一个过程:
(define (search-match . ls)
(define (do-search fix un-fix success fail)
(if (null? un-fix)
(if (< (car fix) (cadr fix))
(success fix)
(fail))
(choose fix (car un-fix) (cdr un-fix) success fail)))
(call/cc
(lambda (success)
(do-search ‘() ls success
(lambda () (error "Search failed"))))))
当 un-fix 为空时, 说明所有值都已经选定, 我们就可以检验值并选择下一步动 作. 吸引我们的是 choose 的实现, choose 要做的工作就是在 un-fix 中的第 一项里选定一个值, 放到 fix 中, 然后递归地调用 do-search 进入下一层递归 . 在 C 中, 它的工作是用循环完成的, 在 Scheme 中, 它却是这么一个递归的 过程:
我们在上面说过将一个循环转换成递归的过程, 现在大家就要把这个递归重新化 为我们熟悉的循环了. (prev-fail) 相当于 C 中循环结束后自然退出, 这退到 了上一个回溯点. 而下面 call/cc 的过程在递归 do-search 的时候创建了一个 回溯点. 比如, 在 do-search 中运行 (fail), 就会回溯回这里, 递归地调用 choose 来选定下一个值.
大家可以写出相应的 C 程序进行对照, 应该能够理解到 fail 参数在这里的使 用. 其实这样回溯实现确实是比较啰嗦的 --- 但是, 如果我们能不写任何代码, 让机器自动完成这样的搜索计算呢?
简言之, 我们只需要一个函数
(define (test a b) (< a b))
然后给定 a, b 的可选范围, 然后系统就告诉我们 a b 的值, 我们不用关心它 是怎么搜索出来的.
有这东西么? 在 Scheme 中请相信奇迹, 用 continuation 可以方便地实现这样 的系统. 下面, 我们要介绍这个系统, 一个 continuation 的著名应用 --- amb 操作符实现非确定计算.
amb 操作符是一个通用的搜索手段, 它实现这样一个非确定计算: 一个函数有 若干参数, 这些参数并没有一个固定的值, 而只给出了一个可选项列表. 系统能 自动地选择一个合适的组合, 以使得函数能正确执行到输出合法的结果.
我们用 (amb 1 2 3) 这样的形式去提供一个参数的可选项, 而 (amb) 则表示没 有可选项, 计算失败. 所以, 所谓一个函数能正确执行到输出合法结果, 就是指 函数能返回一个确定值或一个 amb 形式提供的不确定值; 而函数没有合法结果, 或是计算失败, 就是指函数返回了 (amb). 系统能自动选择/搜索合适的参数组 合, 使函数执行到合适的分支, 避免计算失败, 到最后正确输出结果 --- 其实 说了这么多, 就是一个对函数参数组合的搜索 --- 不过它是全自动的. 比如:
(define (test-amb a b)
(if (< a b)
(list a b)
(amb)))
(test-amb (amb 4 2 3) (amb 1 2 3))
有了上面的基础, 我们知道用 continuation 可是方便地实现它, amb 操作其实 是上面的搜索过程的通用化. 不同的是, 在这里, 给出可选参数的形式更加自由 , 像上面把参数划分为 fix 和 un-fix 的方法不适用了.
我们使用一个共享的回溯点的栈来解决问题. 在执行 (amb 4 2 3) 的时候, 我 们就选定 4, 然后设置一个回溯点, 压入栈中, 执行 (amb 1 2 3) 时也如此 . 而当计算失败要重新选择时, 我们从栈中 POP 出回溯点来跑. 我们注意 (amb 1 2 3) 选择完 3 之后的情况, 在上面的 search-match 实现中, 这相当于 choose 中的 (prev-fail) 语句. 但是 (amb 1 2 3) 并不知道 (amb 4 2 3) 的 存在, 无法这么做, 而借助这个共享栈, 我们可以获得 (amb 4 2 3) 的回溯点, 使计算继续下去. 用这样的方法, 我们就无须使用严密控制的 fix 和 un-fix, 能够自由使用 amb.
我们的整个实现如下, 过程并不复杂, 不过确实比较晦涩, 所以也附带了注释:
(define fail-link ‘()) ; fail continuation 栈
;; amb-fail 在失败回溯时调用, 它另栈顶的 fail continuation 出栈
;; 并恢复到那个 continuation 中去
(define (amb-fail)
(if (null? fail-link)
(error "amb process failed")
(let ((prev (car fail-link)))
(set! fail-link (cdr fail-link))
(prev))))
(define (amb . ls)
(define (do-amb success curr)
(if (null? curr)
(amb-fail) ; 没有可选项, 失败
(begin
(call/cc
(lambda (fail)
(set! fail-link (cons fail fail-link)) ;设置回溯
;; 返回一个选项到需要的位置
(success (car curr))))
;; 回溯点
(do-amb success (cdr curr)))))
(call/cc
(lambda (success)
(do-amb success ls))))
我们可以再敲入上面 test-amb 那段程序看看效果. 我们发现, 其实我们写 (amb) 的时候, 做的就是上面 search-match 实现中的 (fail), 那么整个过程 又可以套回到上面的实现上去了. 以上程序的执行流程分析有点难, 呵呵, 准备 几张草稿纸好好画一下就能明白了.
终章的名实之辩
================= End
开始之前
这是一篇 Scheme 的介绍文章. Scheme 是一个 LISP 的方言, 相对于 Common LISP 或其他方言, 它更强调理论的完整和优美, 而不那么强调实用价值. 我在 学习 Scheme 的时候, 常想的不是 "这有什么用", 而是 "为什么" 和 "它 的本质是什么". 我觉得这样的思考对学习计算机是非常有益的.
我不知道 "Scheme 之道" 这个题目是否合适, 我还没到能讲 "XXX 之道" 的时候. 但 Scheme 确实是一个极具哲学趣味的语言, 它往往专注于找出事物的 本质, 用最简单, 最通用的方法解决问题. 这样的思路下, 我们会碰到许多以往 不会遇到, 或不甚留意的问题, 使我们对这些问题, 以及计算机科学的其他方面 有新的认识和思考.
讲 Scheme 的好书有很多, 但 Scheme 在这些书中往往就像指着月亮的慧能的手 指或是道家的拂尘, 指引你发现计算机科学中的某些奇妙之处, 但 Scheme 本身 却不是重点. 如SICP (Structure and Interpretation of Computer Programs) 用 Scheme 来指引学生学习计算机科学中的基本概念; HTDP (How to design programs) 用Scheme 来介绍程序设计中常用的技巧和方法. 而这篇文章, 着眼点 也不是scheme 本身, 或者着眼点不在 scheme 的 "形", 而在与 scheme 的 "神". 怎么写一个好的 scheme 程序不是我的重点, 我的重点是 "这个设计真 美妙", "原来本质就是如此", 如是而已. Scheme 的一些理论和设计启发了我 , 使我在一些问题, 一些项目上有了更好的想法. 感念至今, 所以写一系列小文 将我的体会与大家分享.
要体验 Scheme, 当然首先要一个 Scheme 的编程环境. 我推荐 drScheme (http://www.drscheme.org), 跨平台, 包括了一个很好的编辑和调试界面 . Debian/Ubuntu 用户直接 apt-get 安装即可.
希望读者有基本的编程和数据结构知识. 因为解释 Scheme 的很多概念时, 这些 知识是必须的.
数据结构的本质论
世界的终极问题
这两个可能是人类对世界认识的终极问题: 世界上最基本的, 不可再分的物质单 位是什么? 这些最基本的物质单位是怎么组成这个大千世界的?
Scheme 也在试图解答这个问题.
Scheme 认为以下两种东西是原子性的, 不可再分的: 数, 符号. 数这个好理解, 符号这个概念就有点麻烦了. 做个比方, "1" 是一个数字, 但它其实是一个符 号, 我们用这个符号去代表 "1" 这个概念, 我们也可以用 "一" 或 "one" 代表这个概念, 当然 "1" 也可以表示 "真" 的概念, 或者什么都 不表示. 而 kyhpudding 也是一个 Scheme 中的符号, 它可以代表任何东西, Scheme 能理解的或不能理解的. 这都没所谓, Scheme 把它作为一个原子单位对 它进行处理: 1 能跟其他数字作运算得出一个新的数字, 但 1 始终还是 1, 它 不会被分解或变成其他什么东西, 作为符号的 kyhpudding 也大抵如此.
下一个问题是: 怎么将原子组成各种复合的数据结构 --- 有没有一种统一的方 法?
我们从最简单的问题开始: 怎么将两个对象聚合在一起? 于是我们引入了 "对 " (pair) 的概念, 用以聚合两个对象: a 和 b 组成的对, 记为:
如果是要聚合三个或以上的数据呢? pair 的方法还适用吗? 我们是否需要引入 其他方法? 答案是不需要, 我们递归地使用 pair 结构就可以了. 聚合 a, b, c, 记为 (a . (b . c)), 它的简化记法是 (a b . c).
大家都能想到了, 递归地使用 pair 二叉树的结构, 就能表达任意多个对象组成 的序列. 比如 (a b . c), 画图就是:
请大家继续将头左侧 45 度. 这样的一个表示序列的树的特点是, 树的左结点是 成员对象, 右结点指向一颗包含其他成员的子树. 但大家也发现了一个破例: 图 中的 c 是右边的叶子. 解决这个问题的办法是: 我们引入一个 "无" 的概念:
这个无的概念我们用 "()" 来表达 (总不能什么都没有吧). 记 (a . ()) 为 (a). 那么上图就可以表示为 (a b c). 这样的结构我们就叫做列表 --- List. 这是 Scheme/LISP 中应用最广的概念. LISP 其实就是 "LISt Processing" 的意思.
这样的结构表达能力很强, 因为它是可递归的, 它可以表达任何东西. 比方说, 一个普通的二叉树可以像这样表示 (根 (根 左子树 右子树) 右子树). 大家也 可以想想其他的数据结构怎么用这种递归的列表来表示.
开始编程啦
好了, 我们可以开始写一点很简单的 Scheme 程序. 比方说, 打入 1, 它就会返 回 1. 然后, 打入一个列表 (1 2), 出错鸟... 打入一个符号: kyhpudding, 也 出错鸟......
于是我们就要开始讲一点点 Scheme 的运作原理了. 刚才我们讲了 Scheme 中的 数据结构, 其实不但是 Scheme 处理的数据, 整个 Scheme 程序都是由这样的列 表和原子对象构成的, 一个合法的 Scheme 数据结构就是一个 Scheme 语句. 那 么这样的语句是怎么运行的呢? 总结起来就是三条逻辑:
- 如果那是一个数, 则返回这个数
- 如果那是一个符号, 则返回该符号所绑定的对象. (这个概念我们会迟点解释)
- 如果那是一个列表, 把列表的第一项作为方法, 其他作为参数, 执行之.
所以, 我们可以试试这个 (+ 1 2), 这下就能正确执行了.
那么, 如果我就想要他返回 (+ 1 2) 这个列表呢? 试试这样 (quote (+ 1 2)) quote 是一个很特殊的操作, 意思是它的参数不按规则处理, 而是直接作为数据 返回. 我们会常常用到它, 所以也有一个简化的写法 ‘(+ 1 2), 在前面加一个 单引号就可以了. 这样子, ‘kyhpudding 也能有正确的输出了.
那么我们可以介绍三个原子操作, 用以操纵列表. 其实, 所谓操纵列表, 也只是 操纵二叉树而已. 所以我们有这么三个操作:
- cons: 将它的两个参数组合起来, 形成新的二叉树/pair
- car: 返回参数的左子树
- cdr: 返回参数的右子树
通过以下几个操作, 结合对应的二叉树图, 能比较好的理解这个 Scheme 最基础 的设计:
无处不在的函数
基本的函数概念
Scheme 是一门函数式语言, 因为它的函数与数据有完全平等的地位, 它可以在 运行时被实时创建和修改. 也因为它的全部运行都可以用函数的方式来解释, 莫 能例外.
比方说, 把 if 语句作为函数来解释? (if cond if-part else-part) 是这么一 个特殊的函数: 它根据 cond 是否为真, 决定执行并返回 if-part 还是 else-part. 比如, 我可以这样写:
if 函数会根据我开心与否 (i-am-feeling-lucky 是一个由我决定它的返回值的 函数 :P) 返回 + 或 - 来作为对我的开心值的操作. 所谓无处不在的函数, 其 意义大抵如此.
把一串操作序列当成函数呢? Scheme 是没有 "return" 的, 把一串操作序列 当作一个整体, 它的返回值就是这一串序列的最后一个的返回值. 比如我们可以 写
它的返回是 7.
无名的能量之源
接下来, 我们就要接触到 Scheme 的灵魂 --- Lambda. 大家可以注意到 drScheme 的图标, 那就是希腊字母 Lambda. 可以说明 Lambda 运算在 Scheme 中是多么重要.
NOTE: 这里本来应该插一点 Lambda 运算的知识的, 但是一来我自己数学就不怎 么好没什么信心能讲好, 二来讲太深了也没有必要. 大家如果对 Lambda 运算的 理论有兴趣的话, 可以自行 Google 相关资料.
Lambda 能够返回一个匿名的函数. 在这里需要注意两点: 第一, 我用的是 "返 回" 而不是 "定义". 因为 Lambda 同样可以看成一个函数 --- 一个能够生 成函数的函数. 第二, 它是匿名的, 意思是, 一个函数并不一定需要与一个名字 绑定在一起, 我们有时侯需要这么干, 但也有很多时候不需要.
我们可以看一个 Lambda 函数的基本例子:
这里描述了一个加法函数的生成和使用. (lambda (x y) (+ x y)) 中, lambda 的第一个参数说明了参数列表, 之后的描述了函数的行为. 这就生成了一个函数 , 我们再将 1 和 2 作用在这个函数上, 自然能得到结果 3.
我们先引入一个 define 的操作, define 的作用是将一个符号与一个对象绑定 起来. 比如
我们自然也可以用 define 把一个符号和函数绑定在一起, 就得到了我们常用的 有名函数.
做一个简单的替换, 上面的例子就可以写成 (add 1 2), 这样就好理解多了.
上面的写法有点晦涩, 而我们经常用到的是有名函数, 所以我们有一个简单的写 法, 我们把这一类简化的写法叫 "语法糖衣". 在前面我们也遇到一例, 将 (quote x) 写成 ‘x 的例子. 上面的定义, 我们可以这样写
Lambda 运算有极其强大的能力, 上面只不过是用它来做传统的 "定义函数" 的工作. 它的能力远不止如此. 这里只是举几个小小的例子:
我们经常会需要一些用于迭代的函数, 比如这个:
我们也需要减的, 乘的, 还有其他各种乱七八糟的操作, 我们需要每次迭代不是 1, 而是 2, 等等等等. 我们很自然地有这个想法: 我们写个函数来生成这类迭 代函数如何? 在 Scheme 中, 利用 lambda 运算, 这是可行且非常简单的. 因为 在 Scheme 中, 函数跟普通对象是有同样地位的, 而 "定义" 函数的 lambda, 其实是能够动态地为我们创造并返回函数对象的. 所以我们可以这么写:
这个简单的例子, 已经能够完成我们在 C 之类的语言无法完成的事情. 要生成 上面的 inc 函数, 我们可以这么写:
这个例子展示的是 Scheme 利用 Lambda 运算得到的能力. 利用它, 我们可以写 出制造函数的函数, 或者说制造机器的机器, 这极大地扩展了这门语言的能力 . 我们在以后会有更复杂的例子.
接下来, 我们会介绍 Scheme 的一些语言特性是怎么用 Lambda 运算实现的 --- 说 Scheme 的整个机制是由 Lambda 驱动的也不为过.
比如, 在 Scheme 中我们可以在任何地方定义 "局部变量", 我们可以这么写:
其实 let 也只不过是语法糖衣而已, 因为上面的写法等价于:
一些常用的函数
虽然说这篇文章不太注重语言的实用性. 但这里还是列出我们经常用到的一些操 作, 这能极大地方便我们的编程, 大家也可以想想他们是怎么实现的.
cond
相当于 C 中的 switch
循环语句
没有循环语句...... 至少没有必要的循环语句. Scheme 认为, 任何的循环迭代 都可以用递归来实现. 我们也不用担心递归会把栈占满, 因为 Scheme 会自动处 理尾递归的情况. 一个简单的 0 到 10 迭代可以写成这样.
很明显, 当我们递归调用 iterate 的时候, 我们不必保存当前的函数环境. 因 为我们递归调用完毕后就马上返回, 而不会再使用当前的环境, 这是一给尾递归 的例子. Scheme 能自动处理类似的情况甚至做一些优化, 不会浪费多余的空间, 也不会降低效率. 所以完全可以代替循环.
当然我们有些便于循环迭代的操作, 大家可以试试自己实现他们. (当然在解释 器内部通常不会用纯 scheme 语句实现他们). 我们最常用的是 map 操作
运行一下这个例子, 就能理解 map 的作用了.
更多的数据操作
- cadr cddr caddr 之类, 就是 car 和 cdr 的组合, 大家可以一个个试 . drScheme 支持到 cadddr...
- append: 将两个列表拼接在一起.
无始无终的太极
我想其他语言的入门教程都不会有这么一节: 这门语言的运作原理是怎么样的 . 但这么一节内容是 Scheme 的入门教程必有的. Scheme 把它最核心, 最底层 的机制都提供出来给用户使用, 使它有非常强大的能力. 所以知道它的运行机理 是非常重要的.
这一节和下一节都是在分析 Scheme 的运行原理. 在这一节中, 我们会用一个太 极图来分析一条 Scheme 语句是怎么被执行的. 在下一节, 我们会在这一节的基 础上引入 Scheme 的对象/内存管理机制. 从而得到一个比较完整的 Scheme 运 行原理, 并用 Scheme 语言表示出来.
我们先从 eval 和 apply 的用法说起. eval 接受一个参数, 结果是执行那个参 数的语句, 而 apply 则接受两个参数, 第一个参数表示一个函数, 第二个参数 是作用于这个函数的参数列表. 例如:
我们可以轻易发现, 这两者是可以轻易转化的:
但是显然, 真正的实现不可能如此, 不然 eval 一次就没完没了地转圈了. 我们 在前面提到 Scheme 的基本运行逻辑, 其实也是 eval 的基本原理:
- 如果那是一个数, 则返回这个数
- 如果那是一个符号, 则返回该符号所绑定的对象.
- 如果那是一个列表, 把列表的第一项作为方法, 其他作为参数, 执行之.
我们来实现一个这样的逻辑, 要注意的是, 下面的 eval 和 apply 的写法都只 是说明概念, 并不是真实可运行的. 但用 Scheme 写一个 Scheme 解释器是确实 可行的:
在第三项, 我们很自然地用了 apply 来实现. 注意 apply 接受的第一个参数必 须是一个函数对象, 而不能是一个类似 add 的名字, 所以我们要递归地调用 eval 解析出它的第一个参数. 那么 apply 要怎么实现呢? 我们来看一个实例:
用 eval 执行它的时候, 会执行
在执行它的时候 , 为了运行它, 我们要知道 add 和 x 代表什么, 我们还得知道 (+ y 1) 的结果, 否则我们的计算无法继续下去. 我们用什么来求得这些值呢
--- 显然是eval. 因此 apply 的处理流程大致如下:
我们得到的还是一个互相递归的关系. 不过这个递归是有尽头的, 当我们遇到原 子对象时, 在 eval 处就会直接返回, 而不会再进入这个递归. 所以 eval 和 apply 互相作用, 最终把程序解释成原子对象并得到结果. 这种循环不息的互相 作用, 可以表示为这样一个太极:

这就是一个 Scheme 解释器的核心.
然而, 我们上面的模型是不尽准确的. 比如, (if cond if-part else-part) 把 这个放入 apply 中的话, if-part 和 else-part 都会被执行一遍, 这显然不是 我们希望的. 因此, 我们需要有一些例外的逻辑来处理这些事情, 这个例外逻辑 通常会放在 eval. (当然理论上放在 apply 里也可以, 大家可以试一下写, 不 过这样在 eval 中也要有特殊的逻辑之处 "if" 这个符号所对应的值). 我们 可以把 eval 改成这样
这样我们的逻辑就比较完整了.
另外 apply 也要做一些改动, 对于 apply 的 method, 它有可能是类似 "+" 这样的内置的 method, 我们叫它做 primitive-proceure, 还有由 lambda 定义 的 method, 他们的处理方法是不一样的.
在下一节, 我们就会从 lambda 函数是怎么执行的讲起, 并再次修改 eval 和 apply 的定义, 使其更加完整. 在这里我们会提到一点点 lambda 函数的执行原 理, 这其实算是一个 trick 吧.
我们这样定义 lambda 函数
那么我们在 apply 这个 lambda 函数的时候会发生什么呢? apply 会根据参数 表和参数做一次匹配, 比如, 参数表是 (x y) 参数是 (1 2), 那么 x 就是 1, y 就是 2. 那么, 我们的参数表写法其实可以非常灵活的, 可以试试这两个语句 的结果:
((lambda x x) 1 2) <= 注意两个 x 都是没有括号的哦 ((lambda (x . y) (list x y)) 1 2 3)
这样 "匹配" 的意义是否会更加清楚呢? 由于这样的机制, 再加上可以灵活运 用 eval 和 apply, 可以使 Scheme 的函数调用非常灵活, 也更加强大.
唯心主义的对象管理系统
关于对象
既然这一节我们要讲对象管理系统. 我们首先就要研究对象, 研究在 Scheme 内 部是如何表示一个对象. 在 Scheme 中, 我们的对象可以分成两类: 原子对象和 pair.
我们要用一种办法唯一地表示一个对象. 对原子对象, 这没什么好说的, 1 就是 1, 2 就是 2. 但是对 pair, 情况就比较复杂了.
如果我们修改了 a 的 car 的值, 我们不希望 b 的值也同样的被改变. 因此虽 然 a 和 b 在 define 时的值一样, 但他们不是相同的对象, 我们要分别表示他 们. 但是 在这个时候
a 和 b 应该指的是同一个对象, 不然 define 的定义就会很尴尬 (define 不是 赋值, 而是绑定). 修改了 a 的 car, b 也应该同时改变.
答案很明显了: 对 pair 对象, 我们应把它表示为一个引用 --- 熟悉 Java 的 同学也会知道一个相同的原则: 在 Java 中, 变量可以是一个原子值 (如数字), 或者是对一个复合对象的引用.
在这里我们引入一组操作, 它可以帮助测试, 理解这样的对象系统:
- set!: 不要漏了叹号, 修改一个符号的绑定
- set-car!: 修改 pair 中左边值的绑定
- set-cdr!: 修改 pair 中右边值的绑定
- eq?: 测试两个对象是否相等
- equal?: 测试两个对象的值是否相等.
我们可以进行如下测试:
另外我们可以想想以下操作形成的对象的结构:
它形成的结构应该是这样的
所以 (eq? (cdr a) (cdr b)) 的值应该是真.
lambda 的秘密
接下来我们要研究: Scheme 是怎么执行一个 lambda 函数的? 运行一个 lambda 函数, 最重要的就是建立一个局部的命名空间, 以支持局部变量 --- 对 Scheme 来说, 所谓局部变量就是函数的参数了. 只要建立好这样的一个命名空间, 剩下 的事情就是在此只上逐条运行语句而已了.
我们首先可以看这样的一个例子:
结果当然是 20, 这说明了 Scheme 在运行 lambda 函数时会建立一个局部的命名 空间 --- 在 Scheme 中, 它叫做 environment, 为了与其他的资料保持一致, 我 们会沿用这个说法, 并把它简写为 env. 而且这个局部 env 有更高的优先权 . 那我们似乎可以把寻找一个符号对应的对象的过程描述如下, 这也是 C 语言程 序的行为:
- 先在函数的局部命名空间里搜索
- 如果找不到, 在全局变量中搜索.
但是 Scheme 中, 函数是可以嵌套的:
很好, 这不就是一个栈的结构吗? 我们在运行中维护一个 env 的栈, 搜索一个名 称绑定时从栈顶搜索到栈底就可以了.
这在 Pascal 等静态语言中是可行的 (Pascal 也支持嵌套的函数定义). 但是在 Scheme 中不行 --- Scheme 的函数是可以动态生成的, 这会产生一些栈无法处 理的情况, 比如我们上面使用过的例子:
执行 inc 和 dec 的时候, 它执行的是 (method x step), x 的值当然很好确定 , 但是method 和 step 的值就有点麻烦了. 我们调用 make-iterator 生成 inc 和dec 的时候, 用的是不同的参数, 执行 inc 和 dec 的时候, method 和 step 的值当然应该不一样, 应该分别等于调用 make-iterator 时的参数. 这样的特性 , 就没法用一个栈的模型来解释了.
一个更令人头痛的问题是: 运行 lambda 函数时会创造一个 env, 现在看起来, 这个 env 不是一个临时性的存在, 即使是在函数执行完以后, 它都有存在的必要 , 不然像上例中, inc 在运行时就没法正确地找到 + 和 1 了. 这是一种我们从 未遇到的模型.
我们要修改函数的定义. 在 Scheme 中, 函数不仅是一段代码, 它还要和一个 environment 相连. 比如, 在调用 (make-iterator + 1) 的时候, 生成的函数要 与执行函数 make-iterator 实时产生的 env 相连, 在这里, method = +, step = 1; 而调用 (make-iterator - 1) 的时候, 生成的函数是在与另一个 env --- 第二次调用 make-iterator 产生的 env 相连, 在这里, method = -, step = 1. 另外, 各个 env 也是相连的. 在执行函数 inc 时, 他会产生一个含有名称 x 的 env, 这个 env 要与跟lambda 函数相连的的 lambda 相连. 这样我们在只 含有 x 的 env 中找不到method, 可以到与其相连的 env 中找. 我们可以画图如 下来执行 (inc 10) 时的 env 关系:
inc: ((x 10)) -> ((method +) (step 1)) -> ((make-iterator 函数体))
这里的最后一项就是我们的全局命名空间, 函数 make-iterator 是与这个空间 相连的.
于是我们可以这样表示一个 env 和一个 lambda 函数对象: 一个 env 是这么一 个二元组 (名称绑定列表 与之相连的上一个 env). 一个 lambda 是一个这样的 三元组: (参数表 代码 env).
由此我们需要修改 eval 和 apply. 解释器运行时, 需要一直保持着一个 "当 前 env". 这个当前 env 应该作为参数放进 eval 和 apply 中, 并不断互相传 递. 在生成一个 lambda 对象时, 我们要这样利用 env:
这样就可以表示 lambda 函数与一个 env 的绑定. 那么我们执行 lambda 函数 的行为可以这么描述:
这样我们就可以完全清楚的解释 make-iterator 的行为了. 在执行 (make-iterator + 1) 时, make-env 生成了这样的一个 new-env:
这个 new-env 会作为参数 env 去调用 eval. 在 eval 执行到 lambda 一句时, 又会以这样的参数来调用 make-lambda, 因此这样的一个 env 就会绑定到这个 lambda 函数上. 同理, 我们调用 (make-iterator - 1) 的时候, 就能得到另一 个 env 的绑定.
这种特性使 "函数" 在 scheme 中的含义非常丰富, 使用非常灵活, 以下这个 例子实现了非常方便调试的函数计数器:
用普通的参数调用 add 时, 它会执行一个正常的加法操作. 但如果调用 (add ‘print), 它就会返回这个函数被执行了多少次. 这样的一个测试用 wrapper 是 完全透明的. 正因为 scheme 函数可以与一个 env, 一堆值相关联, 才能实现这 么一个功能.
自动垃圾收集
我们的问题远未解决.
C 语言中, 局部变量放在栈中, 执行完函数, 栈顶指针一改, 这些局部变量就全 没了. 这好理解得很. 但根据我们上面的分析, Scheme 中的函数执行完后, 它 创造的 env 还不能消失. 这样的话, 不就过一会就爆内存了么......
所以我们需要一个自动垃圾收集系统, 把用不着的内存空间全部收回. 大家可能 都是在 Java 中接触这么一个概念, 但自动垃圾收集系统的祖宗其实是 LISP, Scheme 也继承了这么一个神奇的系统.
自动垃圾收集系统可以以一句唯心主义的话来概括: 如果你没法看到它了, 它就 不存在了. 在 Java 中, 它似乎是一个很神奇的机制, 但在 Scheme 中, 它却简 单无比.
我们引入上下文的概念: 一个上下文 (context), 包括当前执行的语句, 当前 env, 以及上一个与之相连的 context --- 如我们所知, 在调用 lambda 函数时 , 会产生一个新的 env, 但其实它也产生一个新的 context, 包括了 lambda 中 的代码, 新的 env, 以及对调用它的 context 的引用 (这就好比在 x86 中调用 CALL 指令压栈的当前指令地址, 在使用 RET 的时候可以弹出返回正确的地方 ). 它是这样的一个三元组: (code env prev-context). 任何时候, 我们都处于 一个这样的上下文中.
引入这个概念, 是因为一个 context, 说明了任何我们能够访问和以后可能会访 问的对象集合: 正要运行的代码当然是我们能访问的, env 是所有我们能够访问 的变量的集合, 而 prev-context 则说明了我们以后可能能够访问的东西: 在函 数执行完毕返回后, 我们的 context 会恢复到 prev-context, prev-context 包含的内容是我们以后可能访问到的.
如上所述, code, env, 以及 context 本身都可以描述为标准的 LIST 结构, 那 我们所谓能 "看到" 的对象, 就是当前 context 这个大表中的所有内容. 其 他的东西, 都是垃圾, 要被收走.
比如, 我们处在 curr-context 中, 调用 (add 1 2). 那会产生一个新的 new-context, 在执行完 (add 1 2) 后, 我们又回到了 curr-context, 它与 new-context 不会有任何的联系 --- 我们无论如何也不可能在这里访问到执行 add 时的局部变量. 所以执行 add 时产生的 env 之类, 都会被当作垃圾收走.
当我们使用的内存多于某个阈值, 自动垃圾收集机制就会启动. 有了上面的介绍 , 我们会发现这么个机制简单的不值得写出来: 当前的 context 是一个 LIST, 遍历这个 LIST, 把里面的所有对象标记为有用. 然后遍历全部对象, 把没有标 记为有用的对象全部当垃圾回收, 完了. 当然真实实现远远不是如此, 会有很多 的优化, 但它的基本理论就是如此.
好了, 我们要再一次修改 eval, apply 和 run-lambda 的实现, 这次要怎么改 动大家都清楚得很了.
通过这次修改, 我们也可以解释自动处理尾递归为什么是可行的. 我们在上面举 出了一个尾递归的例子:
在 C 语言中, 再新的新手也不会写这种狂吃内存的愚蠢代码, 但在 Scheme 中, 它是很合理的写法 --- 因为有自动垃圾收集.
在每次调用函数的时候, 我们可以做这样的分析, iterate 的递归调用图如下:
(iterate 0) -> (iterate 1) -> (iterate 2) ....
| ^ | ^ |
----+ +----------+ +-------------+
下面的箭头表示函数返回的路径. 如果我们每次的递归调用都是函数体中的最后 一个语句, 就说明: 比如从 (interate 2) 返回到 (iterate 1) 时, 我们什么 都不用干, 又返回到 (iterate 0) 了. 在 iterate 中, 我们每一层递归都符合 这个条件, 所以我们就给它一个捷径:
(iterate 0) -> (interate 1) -> ... (interate 10)
|
<-----------------------------------------+
让他直接返回到调用 (iterate 0) 之前. 在实现上, 我们可以这么做: 比如, 我们处在 (iterate 0) 的 context 中, 调用 (iterate 1). 我们把 (iterate 1) 的 context 中的 prev-context 记为 (iterate 0) 的 prev-context, 而不 是 (iterate 0) 的 context, 就能形成这么一条捷径了. 我们每一层递归都这 么做, 可以看到, 其实每一层递归的 context 中的 prev-context 都是调用 (interate 0) 之前的 context! 所以其实执行 (interate 10) 的时候, 与前面 的 context 没有任何联系, 前面递归产生的 context 都是幽魂野鬼, 内存不足 时随时可以回收, 因此不用担心浪费内存. 而 Scheme 自动完成分析并构造捷径 的过程, 所以在 Scheme 中可以用这样的递归去实现迭代而保持高效.
面向对象的 Scheme
我们可以这样定义一个对象: 对象就是数据和在数据之上的操作的集合.
Scheme 中的 lambda 函数, 不但有代码, 还和一个 environment, 一堆数据相 连 --- 那不就是对象了么. 在 Scheme 中, 确实可以用 lambda 去实现面向对 象的功能. 一个基本的 "类" 的模板是类似这样的:
使用
这样就能很方便地把它和其他语言中的对象对应起来了.
Scheme 虽然没有真正的, 复杂的面向对象概念, 没有继承之类的咚咚, 但 Scheme 能够实现更灵活, 更丰富的面向对象功能. 比如, 我们前面举过的 make-counter 的例子, 它就是一个函数调用计数器的类, 而且, 它能提供完全 透明的接口, 这一点, 其他语言就很难做到了.
创造机器的机器
真实存在的时光机器
在上一节中, 我们引入了 context 的概念, 这个概念代表 scheme 解释器在任 何时刻的运行状态. 如果我们有一种机制, 能够把某个时候的 context 封存起 来, 到想要的时候, 再把它调出来, 这一定会非常有趣 --- 对, 就像游戏中的 存档一样. 如果真有这样的机制, 那就简直是真实存在的时光机器了.
Scheme 还真的有这个机制 --- 它把 context 也看成一个对象, 可以由用户自 由地使用, 这使我们能完成很多 "神奇" 的事情. 在上一节, 我们为了方便理 解, 使用了 "context" 这一叫法, 在这里, 我们恢复它的正式称呼 --- 这一 节, 我们研究 continuation.
我们还是从它的用法说起, continuation 的使用从 call-with-current-continuation 开始, 这个名字长得实在难受, 我们按惯例 一律缩写为 call/cc. call/cc 可以这样使用
它接受一个函数作为参数, 而这个函数的参数就是这个 continuation 对象. 我 们要怎么用这个对象呢? 以下是一个最简单的例子:
大家可以试试它的结果, 与 (+ 1 2) 相同. 这里最重要的一句是 (cont 2). 我 们从一开始就说, Scheme 中的一切都是函数, 在上一节中我们知道, 为了执行一 个函数, 我们创建一个 context (continuation), 那 context 的行为的最终结 果就是返回一个值了. 而 (cont 2) 这样用法相当于是给 cont 这个 continuation 下个断言: 这个 context(continuation) 的返回值就是 2, 不用 再往下算了 --- 我们也可以这么想象, 当解释器运行到 (cont 2) 的时候, 就把 整个 (call/cc ....) 替换成 2, 所以得到我们要的结果.
没什么特别, 对吧. 但这一点点已经能有很重要的应用 --- 我的函数有很多条 语句 (这在 C 等过程式语言中很常见, 在 Scheme 这类语言中倒是少见的), 我 想让它跑到某个点就直接 return; 我需要一个像 try ... catch 这样的例外机 制, 而不想写一个 N 层的 if. 上面的 continuation 用法就已经能做到了, 大 家可以试试写一个 try ... catch 的框架, 很简单的.
老实说, 上面这个一点都不像时光机, 也不见得有多强大. 我们再来点好玩的:
以上这些语句当然不会有执行结果, 因为 call/cc 没有返回任何值给 x, 在 if 语句之后就无法继续下去了. 不过, 在这里我们把这个 continuation 保存成了 一个全局变量 g-cont. 现在我们可以试试: (g-cont 10). 大家可以看到结果了 : 这才是时光机啊, 通过 g-cont, 我们把解释器送回从前, 让 x 有了一个值, 然后重新计算了 let 之中的内容, 得出我们所要的答案.
这样的机制当然不仅仅是好玩的, 它可以实现 "待定参数" 的功能: 有的函数 并不能直接被调用, 因为它的参数可能由不同的调用者提供, 也可能相隔很长时 间才分别提供. 但无论如何, 只要参数一齐, 函数就要马上得到执行 --- 这是 一种非常常见的模块间通讯模式, 但用普通的函数调用方法无法实现, 其他方法 也很难实现得简单漂亮, continuation 却使它变得非常简单. 比如
到我们用类似 (slot-x 10) 的形式提供完整的 x y 参数值后, add 就会正确地 计算. 在这里, add 不用担心是谁, 在什么时候给它提供参数, 而参数的提供者 也不必关心它提供的数据是给哪个函数, 哪段代码使用. 这样, 模块之间的耦合 度就很低, 而依然能简单, 准确地实现功能. 实在非 continuation 不能为也.
不过要注意的是, continuation 并不是真的如游戏的存档一般 --- 我们知道 continuation 的实现, 一个 continuation 只不过是一个简单的对象指针, 它 不会真的复制保存下全部运行状态. 我们保存下一个 continuation, 修改了全 局变量, 然后再回到那个 continuation, 全局变量是不会变回来的. 有了前一 章的知识, 大家很清楚什么才会一直在那里不被改动 --- 这个 continuation 所关联的私有 env 才是不会被改动的.
既然有时光机的特性, continuation 会是一个强力的实现回溯算法的工具. 我们 可以用 continuation 保存一个回溯点, 当我们的搜索走到一个死胡同, 可以退 回上一个保存的回溯点, 选择其他的方案.
比方说, 在 m0 = (4 2 3) 和 m1 = (1 2 3) 中搜索一个组合, 使 m0 < m1, 这 是一个非常简单的搜索问题. 我们递归地先选一个 m0 的值, 再选一个 m1 的值 , 到下一层递归的时候, 由于没有东西可选了. 所以我们检验是否 m0 < m1, 如 果是, 退出, 否则就回溯到上一回溯点, 选择下一个值.
回溯点的保存当然是用 continuation, 我们不但要在一个尝试失败时使用 continuation 作回溯, 还需要在得到正确答案时用 continuation 跳过层层递 归, 直接返回答案.
所以, 我们有这样的一个过程:
(define (search-match . ls)
(define (do-search fix un-fix success fail)
(if (null? un-fix)
(if (< (car fix) (cadr fix))
(success fix)
(fail))
(choose fix (car un-fix) (cdr un-fix) success fail)))
(call/cc
(lambda (success)
(do-search ‘() ls success
(lambda () (error "Search failed"))))))
当 un-fix 为空时, 说明所有值都已经选定, 我们就可以检验值并选择下一步动 作. 吸引我们的是 choose 的实现, choose 要做的工作就是在 un-fix 中的第 一项里选定一个值, 放到 fix 中, 然后递归地调用 do-search 进入下一层递归 . 在 C 中, 它的工作是用循环完成的, 在 Scheme 中, 它却是这么一个递归的 过程:
我们在上面说过将一个循环转换成递归的过程, 现在大家就要把这个递归重新化 为我们熟悉的循环了. (prev-fail) 相当于 C 中循环结束后自然退出, 这退到 了上一个回溯点. 而下面 call/cc 的过程在递归 do-search 的时候创建了一个 回溯点. 比如, 在 do-search 中运行 (fail), 就会回溯回这里, 递归地调用 choose 来选定下一个值.
大家可以写出相应的 C 程序进行对照, 应该能够理解到 fail 参数在这里的使 用. 其实这样回溯实现确实是比较啰嗦的 --- 但是, 如果我们能不写任何代码, 让机器自动完成这样的搜索计算呢?
简言之, 我们只需要一个函数
(define (test a b) (< a b))
然后给定 a, b 的可选范围, 然后系统就告诉我们 a b 的值, 我们不用关心它 是怎么搜索出来的.
有这东西么? 在 Scheme 中请相信奇迹, 用 continuation 可以方便地实现这样 的系统. 下面, 我们要介绍这个系统, 一个 continuation 的著名应用 --- amb 操作符实现非确定计算.
amb 操作符是一个通用的搜索手段, 它实现这样一个非确定计算: 一个函数有 若干参数, 这些参数并没有一个固定的值, 而只给出了一个可选项列表. 系统能 自动地选择一个合适的组合, 以使得函数能正确执行到输出合法的结果.
我们用 (amb 1 2 3) 这样的形式去提供一个参数的可选项, 而 (amb) 则表示没 有可选项, 计算失败. 所以, 所谓一个函数能正确执行到输出合法结果, 就是指 函数能返回一个确定值或一个 amb 形式提供的不确定值; 而函数没有合法结果, 或是计算失败, 就是指函数返回了 (amb). 系统能自动选择/搜索合适的参数组 合, 使函数执行到合适的分支, 避免计算失败, 到最后正确输出结果 --- 其实 说了这么多, 就是一个对函数参数组合的搜索 --- 不过它是全自动的. 比如:
(define (test-amb a b)
(if (< a b)
(list a b)
(amb)))
(test-amb (amb 4 2 3) (amb 1 2 3))
有了上面的基础, 我们知道用 continuation 可是方便地实现它, amb 操作其实 是上面的搜索过程的通用化. 不同的是, 在这里, 给出可选参数的形式更加自由 , 像上面把参数划分为 fix 和 un-fix 的方法不适用了.
我们使用一个共享的回溯点的栈来解决问题. 在执行 (amb 4 2 3) 的时候, 我 们就选定 4, 然后设置一个回溯点, 压入栈中, 执行 (amb 1 2 3) 时也如此 . 而当计算失败要重新选择时, 我们从栈中 POP 出回溯点来跑. 我们注意 (amb 1 2 3) 选择完 3 之后的情况, 在上面的 search-match 实现中, 这相当于 choose 中的 (prev-fail) 语句. 但是 (amb 1 2 3) 并不知道 (amb 4 2 3) 的 存在, 无法这么做, 而借助这个共享栈, 我们可以获得 (amb 4 2 3) 的回溯点, 使计算继续下去. 用这样的方法, 我们就无须使用严密控制的 fix 和 un-fix, 能够自由使用 amb.
我们的整个实现如下, 过程并不复杂, 不过确实比较晦涩, 所以也附带了注释:
(define fail-link ‘()) ; fail continuation 栈
;; amb-fail 在失败回溯时调用, 它另栈顶的 fail continuation 出栈
;; 并恢复到那个 continuation 中去
(define (amb-fail)
(if (null? fail-link)
(error "amb process failed")
(let ((prev (car fail-link)))
(set! fail-link (cdr fail-link))
(prev))))
(define (amb . ls)
(define (do-amb success curr)
(if (null? curr)
(amb-fail) ; 没有可选项, 失败
(begin
(call/cc
(lambda (fail)
(set! fail-link (cons fail fail-link)) ;设置回溯
;; 返回一个选项到需要的位置
(success (car curr))))
;; 回溯点
(do-amb success (cdr curr)))))
(call/cc
(lambda (success)
(do-amb success ls))))
我们可以再敲入上面 test-amb 那段程序看看效果. 我们发现, 其实我们写 (amb) 的时候, 做的就是上面 search-match 实现中的 (fail), 那么整个过程 又可以套回到上面的实现上去了. 以上程序的执行流程分析有点难, 呵呵, 准备 几张草稿纸好好画一下就能明白了.
终章的名实之辩
以上是关于scheme 之门的主要内容,如果未能解决你的问题,请参考以下文章