分布问题(二元,多元变量分布,Beta,Dir)
Posted tectal
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了分布问题(二元,多元变量分布,Beta,Dir)相关的知识,希望对你有一定的参考价值。
这涉及到数学的概率问题。
二元变量分布:
伯努利分布,就是0-1分布(比如一次抛硬币,正面朝上概率)
那么一次抛硬币的概率分布如下:
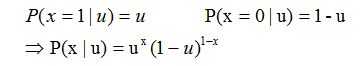
假设训练数据如下:
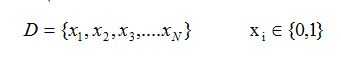
那么根据最大似然估计(MLE),我们要求u:
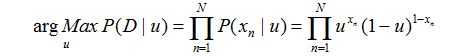
求值推导过程如下:
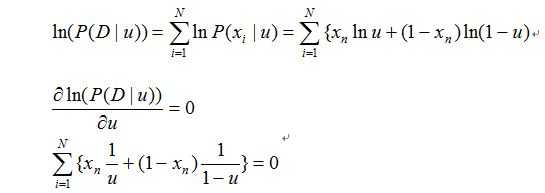
所以可以求出:
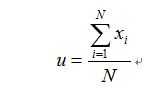
以上的推导过程就是极大似然估计,我们可以看出u就是样本出现的频率除以总共抛硬币的实验次数。但是极大似然估计有它的局限性,当训练样本比较小的时候会导致Overfitting问题,比如说抛了10次硬币,有8次朝上,那么根据极大似然估计,u的取值就应该是8/10(这符号频率派的观点)。如何解决这个问题呢?
那么这时候就需要从贝叶斯理论出发,贝叶斯理论认为,u并不是一个固定的值,u是同样服从某个分布,因此我们假设u有个先验分布P(u)。
但是如何选取这个先验分布p(u)呢?
我们知道
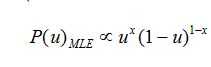
因此我们希望先验分布也可以有类似的概率分布,为什么这么说呢?因为后验概率=先验概率*似然函数,所以如果选择的先验分布和似然函数有一样的结构,那么得到的后验概率也会存在相似的结构,这样会使得我们后面的计算简便。
共轭性:θ的后验分布p(θ|x)与先验分布P(θ)属于同一分布,那么称二者为共轭分布。
因此我们假设u的先验分布也为
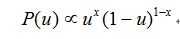
那么这时候数学里面有个分布叫做Beta分布:
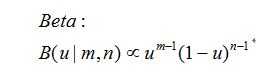
那么假设我们投硬币,m次正面,l次反面。总共是m+l=N次实验:
那么这时候u的分布为:
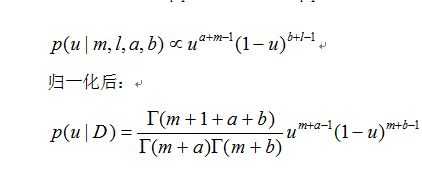
依旧和先验分布服从一样的分布(共轭分布)
假设我们要预测下一次的实验结果,也就是给定D得到下一次的预测分布:
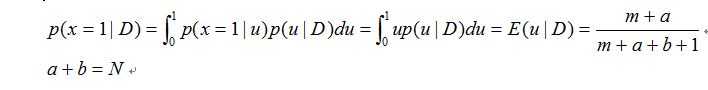
我们可以发现当m,N无限变大的时候,这种估计近似等于极大似然估计。
多元变量分布:
很多时候,变元的不止只有两个,还有多元,其实估计过程是类似的。 假设有k维向量,其中某个向量Xk=1,其他等于0。
例如某个变量x2发生,则X2=1,x=(0,1,0,0,0,0) 以抛筛子为例子,总共有6个面。
那么xk=1发生的概率为Uk,那么x的分布为:
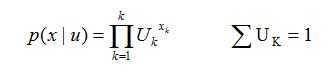
考虑n个独立观测值{x1,x2,...xn}D,对应的似然函数:
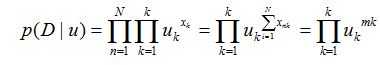
其中mk其实就是这么多次实验中,uk出现的次数大小。估计极大似然估计,我们会得出:
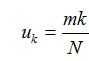
同理,为了避免数据量小导致的过拟合问题,我们对Uk也假设一个先验分布:
考虑到对于多元变量的分布u:
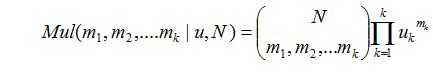
因此我们选择它的共轭分布狄利克雷分布为先验分布:
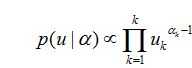
那么后验分布=似然分布*先验分布:
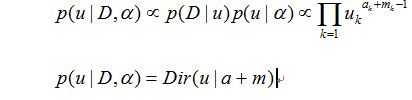
依旧和先验分布服从一样的分布(共轭分布)
假设我们要预测下一次的实验结果,也就是给定D得到下一次的预测分布:
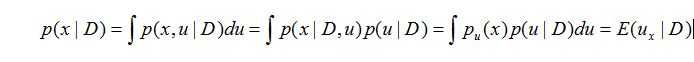
又因为对于狄利克雷分布:
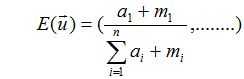
所以对于某个类的分布预测为:
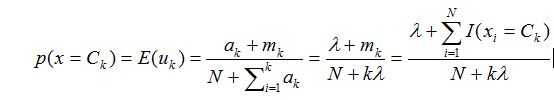
以上是关于分布问题(二元,多元变量分布,Beta,Dir)的主要内容,如果未能解决你的问题,请参考以下文章